Определение характеристик цифровых фильтров

Как известно, для синтеза того или иного вида ЦФ используется ряд этапов [1].

Первый этап заключается в выборе требуемого вида АЧХ идеального фильтра, а именно: нижних частот (ФНЧ), верхних частот (ФВЧ), полосового (ПФ) и режекторного (РФ).

Второй этап заключается в выборе требуемого вида аппроксимации АЧХ, а именно: полиномом Баттерворта (максимально гладкая АЧХ как в полосе пропускания, так и в полосе задержания), полиномом Чебышева I-го типа (пульсации в полосе пропускания и максимальная гладкость в полосе задержания), полиномом Чебышева II-го типа (максимальная гладкость в полосе пропускания и пульсации в полосе задержания) и эллиптическими функциями (пульсации в полосе пропускания и в полосе задержания).

Третий этап заключается в определении вида используемых при построении ЦФ элементарных ячеек.

Четвертый этап заключается в определении порядка аппроксимирующей АЧХ функции и производится вычисление коэффициентов полиномов, однозначно связанных с положением полюсов и нулей на Z-плоскости, по которым определяются коэффициенты конкретных элементарных ячеек.

Пятый этап связан с определения требуемого уровня параллелизма входных данных, зависящих от частоты дискретизации и быстродействия используемых цифровых функциональных узлов.

Шестой этап связан с синтезом распараллеленных структур соответствующих элементарных ячеек.

Седьмой этап связан с настройкой полученного в результате расчетов ЦФ.

Как правило, первый, второй и третий этапы определяются при формирования технического задания и задаются. Четвертый этап определяет все электрические параметры фильтров. Пятый и шестой этапы необходимы тогда, когда недостаточна производительность и быстродействие используемой элементной базы. Седьмой этап характерен для этапа изготовления ЦФ.

Предварительный расчет ЦФ заключается в определении его порядка по заданному виду аппроксимирующей АЧХ функции. Для этого необходимо иметь информацию по следующим параметрам:

тип фильтра – ФНЧ, ФВЧ, ПФ или РФ;

вид аппроксимации АЧХ – полиномом Баттерворта, Чебышева I-го или II-го типов, эллиптическими функциями;

частота дискретизации 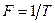в Гц или период дискретизации 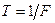в секундах;

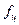частота настройки в Гц (для ПФ и РФ);

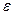величина затухания на крайней частоте полосы пропускания;

величина затухания 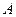на крайней частоте переходной полосы;

ширина полосы пропускания 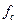на уровне 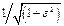в Гц (для ФНЧ и ПФ);

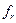ширина переходной полосы на уровне 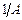в Гц (для ФНЧ и ПФ);

ширина полосы режекции 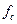на уровне 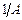в Гц (для ФВЧ и РФ);

ширина переходной полосы 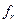на уровне 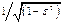в Гц (для ФВЧ и РФ).

Расчет порядка ЦФ осуществляется по выражениям, приводимым на стр. 166-170 в [1].

Пример 8. По заданным параметрам ЦФ рассчитать его порядок 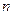и представить его структурную схему в виде каскадного включения звеньев, изображенных в виде квадратов. Нарисовать качественную картину АЧХ рассчитанного ЦФ.

Параметры ЦФ.

тип фильтра – РФ;

вид аппроксимации АЧХ – полином Баттерворта;

частота дискретизации 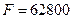Гц;

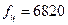частота настройки Гц;

величина ;

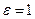величина ;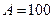

ширина полосы режекции 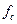=1570 Гц на уровне ;

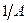ширина переходной полосы 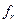=3140 Гц на уровне .

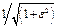В соответствии с выражениями, приводимыми в [1] на стр. 167 в табл. 6.1, определяем нормированные параметры

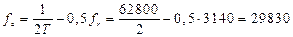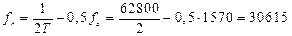Гц;

Гц.

Далее используем выражения, приводимые в [1] на стр. 168 в табл. 6.2, для определения величины .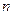

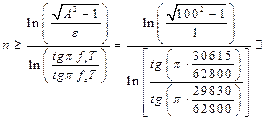
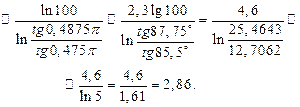
Следовательно, порядок режекторного ЦФ должен быть равен ближайшему большему целому числу, т.е.

.

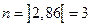На рис. 12. изображена структурная схема рассчитанного цифрового РФ в виде каскадного соединения 3-х квадратов.

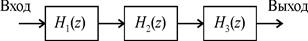Рис. 12. Структурная схема рассчитанного режекторного ЦФ, выполненная в виде каскадного соединения квадратов

На рис.13 изображена качественная картина АЧХ рассчитанного цифрового РФ.

Рис. 13. Качественная картина АЧХ рассчитанного цифрового режекторного фильтра

Аналогичным образом решаются все задачи в п.10.1.7. в [2].