Методы и устройства цифровой обработки сигналов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Технологический институт

Федерального государственного образовательного

учреждения высшего профессионального образования

«Южный федеральный университет»

В.И.Литюк

СБОРНИК РЕШЕНИЙ ЗАДАЧ

По курсу

МЕТОДЫ И УСТРОЙСТВА ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

В РАДИОПРИЕМНЫХ УСТРОЙСТВАХ

Учебное пособие

Таганрог 2009

УДК 621.391.23(075.8)

Литюк В.И. Сборник решений задач по курсу «Методы и устройства цифровой обработки сигналов в радиоприемных устройствах»: Учеб. пособие. – Таганрог: Изд-во Технологического института ЮФУ, 2009. – 64 с.

ISBN .-. . . . - . . . . - .

В данном пособии приводятся основные теоретические сведения для типовых задач, с которыми наиболее часто встречаются студенты на практических занятиях и при выполнении контрольных работ. Приведены конкретные математические соотношения, позволяющие проводить решение соответствующих задач. Даются комментарии к решениям рассмотренных типовых задач, встречающихся на практике.

Пособие предназначено для студентов старших курсов радиотехнических специальностей и может быть использовано при подготовке дипломных проектов, работ, подготавливаемых для получения академических степеней «Бакалавр техники и технологий» и «Магистр техники и технологий» по направлению 552500 «Радиотехника». Пособие может быть полезным для аспирантов и специалистов, работающих в области цифровой обработки сигналов.

Ил. 22. Библиогр.: 3 назв.

Печатается по решению редакционно-издательского совета Технологического института Южного федерального университета.

Рецензенты:

В.П.Федосов, заведующий кафедрой теоретических основ радиотехники Технологического института в городе Таганроге Южного федерального университета, д-р техн. наук, профессор.

В.П.Карелин, заведующий кафедрой математики и информатики Таганрогского института управления и экономики, д-р техн. наук, профессор.

Б.Г.Фрадкин, канд. техн. наук, главный специалист ОКБ ОАО «Таганрогский завод “Прибой”».

ISBN .-. . . . - . . . . - . © Технологический институт

Южного федерального университета, 2009

ВВЕДЕНИЕ

В настоящее время цифровая обработка сигналов (ЦОС) позволяет решать в реальном масштабе времени все более широкий круг различных радиотехнических задач. При этом независимо от вида конкретной задачи, при обработке аналоговых сигналов, поступающих с выхода линейных трактов того или иного радиоприемного устройства (РПрУ), при реализации алгоритмов ЦОС всегда осуществляется ряд преобразований [1].

К таким преобразованиям относят:

аналого-цифровое преобразование аналогового сигнала, поступающего с выхода линейного тракта РПрУ, в цифровую форму;

вычисления для линейных цифровых систем по соответствующему алгоритму дискретного аналога интеграла свертки;

вычисление тех или иных нелинейных преобразований, в частности, выполнение операции извлечения корня квадратного из суммы квадратов квадратурных составляющих обработанного сигнала;

цифроаналоговое преобразование обработанного сигнала из цифровой формы в аналоговую.

В данном пособии рассматриваются типовые задачи, которые решаются студентами на практических занятиях и во время самостоятельной проработки курса ЦОС в соответствии с заданиями, приводимыми в [2].

АНАЛОГО-ЦИФРОВОЕ ПРЕОБРАЗОВАНИЕ СИГНАЛОВ

Как известно, на выходе линейного тракта РПрУ аналоговый сигнал представляет собой комплексный узкополосной случайный процесс 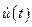, который может быть представлен в виде 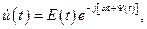[1]

(1.1)

где 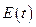– огибающая процесса (В); 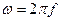– угловая частота процесса (рад/с); 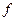– частота, которую обычно полагают равной промежуточной частоте РПрУ (Гц); 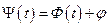– полная фазовая процесса (рад); 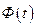– закон фазовой модуляции процесса (рад); 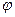– начальная фаза (рад).

При многоразрядном представлении в цифровой форме процесса (1.1), частота выборок которого определяется условиями теоремы Котельникова, производится обработка реального и мнимого квадратурных отсчетов в виде

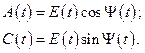(1.2)

Отметим, что огибающая и полная фазовая функция в выражении (1.1), описывающим сигнал в полярной системе координат, также как и квадратурные составляющие в (1.2), описывающие этот же сигнал в декартовой системе координат, связаны между собой соответствующими преобразованиями Гильберта [1].

В реальных условиях полагают, что ширина спектра обрабатываемого процесса полагается равной величине 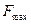, при которой интенсивность спектральных компонент квадратурных составляющих полезного сигнала становится меньше интенсивности аддитивного шума, поступающего на обработку вместе с полезным сигналом.

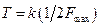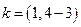В реальных условиях период дискретизации , где коэффициент, показывающий, во сколько раз период дискретизации меньше величины, определяемой из условий выполнения теоремы Котельникова.

Очевидно, что чем ближе коэффициент 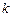к единице, чем менее высокие требования предъявляются к аналого-цифровым преобразователям (АЦП).

В дальнейшем в рассматриваемых задачах всегда будем полагать, что величина 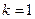, что соответствует идеальному случаю.

Обычно полагают, что с выхода линейного тракта РПрУ поступает помеховая реализация в виде «белого» шума, характеристики которого определяются его интенсивностью или дисперсией 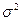(Вт или В²), где 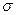(В) – величина среднеквадра-тического отклонения.

Для выбора характеристик АЦП, которые определяют качество преобразования входного процесса из аналоговой формы в цифровую, необходимо иметь ряд данных.

Обычно полагают, что сетка уровней квантования равномерно перекрывает весь динамический диапазон РПрУ. При этом величину шага квантования по амплитуде 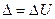(В) обычно нормируют относительно величины среднеквадра-тического отклонения «белого» шума на выходе линейного тракта РПрУ 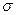(В), т.е. полагают, что

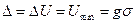(В), (1.3)

где 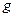– числовой коэффициент, показывающий, во сколько раз величина 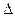(В) больше, равна или меньше величины 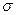(В).

Очевидно, что число уровней квантования АЦП будет

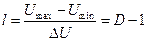, (1.4)

где 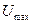(В) и 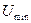(В) – максимальная и минимальная величины входного сигнала; 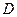– динамический диапазон входного сигнала в разах относительно величины младшего разряда АЦП.

Связь динамического диапазона входного сигнала 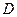(раз), определяемого выражением (1.4), с разрядностью преобразования 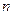определяется выражением

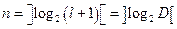. (1.5)

Здесь знак 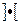в выражении (1.5) означает ближайшее большее целое число, т.е. не меньшее числа, находящегося внутри обратных квадратных скобок.

Связь динамического диапазона входного сигнала 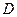в разах с динамическим диапазоном входного сигнала 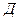в децибелах определяется выражением

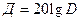(дБ). (1.6)

Число децибел динамического диапазона 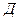входного сигнала, приходящегося на один разряд [3]

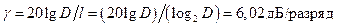. (1.7)

Обычно вместо выражения (1.7) пользуются при расчетах приближенным значением

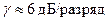. (1.8)

Тогда с учетом выражений (1.6) и (1.8) количество разрядов 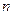АЦП можно определить по выражению

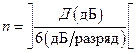разрядов. (1.9)

Число уровней квантования в применяемом АЦП, определяется выражением

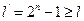. (1.10)

Мощность шума квантования, вносимого АЦП в преобразуемый входной сигнал, определяется величиной

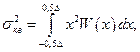(1.11)

где 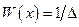– плотность распределения амплитуды входного сигнала в пределах шага квантования АЦП, равного .

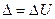Решая выражение (1.11), получим

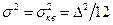. (1.12)

Используя выражение (1.12) можно определить величину среднеквадратического отклонения 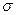в виде

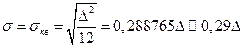. (1.13)

Если выбрать величину 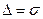, т.е. в выражении (1.3) 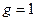, то мощность шумов АЦП, добавляемых к шумам, присутствующим на выходе линейного тракта РПрУ, увеличит суммарную мощность на 8,33%.

В случае, когда 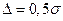, т.е. в выражении (1.3) 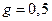, то суммарная мощность шумов возрастет на 2,1%.

Максимальная величина аналогового сигнала, которую может преобразовать в цифровой код рассчитанный АЦП, с учетом (1.10), определяется в соответствии с выражением

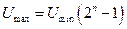(В). (1.14)

Пример 1.Рассчитать, сколько разрядов АЦП 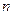потребуется для заданного динамического диапазона 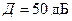входного сигнала. Определить погрешности, вносимые АЦП в преобразуемый сигнал (величину дисперсии 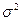(В²) и величину среднеквадратического отклонения 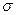(В)). Определить величину 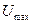(В) при условии, что 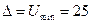мВ.

Количество разрядов 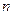в соответствии с выражением (1.9) будет

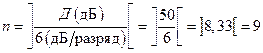разрядов.

Определим величину дисперсии 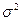(Вт) в соответствии с выражением (1.12) при условии, что 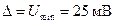= = 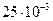В

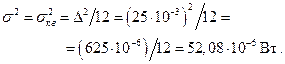
Величина среднеквадратического отклонения 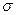(В) определим в соответствии с выражением (1.13)

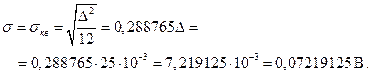
Максимальная величина входного сигнала 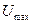(В) определим из выражения (1.14)

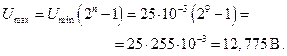
Таким образом, в результате расчетов получены значения:

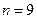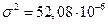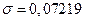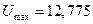; Вт; В; В.

Аналогичным образом решаются все задачи в п.10.1.3. в [2].

В том случае, когда нет возможности учесть шум, сопровождающий сигнал, как, например, в системах автоматики, то в этом случае задаются точностью 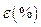представления полезного сигнала, имеющего минимальную величину .

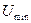Например, пусть величина 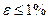. Тогда, поскольку 1%=0,01<128=2^-7, то 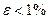, а, следовательно, минимальный сигнал преобразуется в АЦП с заданной точностью при использовании 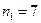разрядов.

Если динамический диапазон входного сигнала в этом случае равен 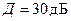, то потребуется еще

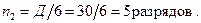
Следовательно, общее число разрядов 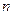АЦП будет равно

.

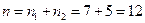ЛИНЕЙНЫЕ ЦИФРОВЫЕ СИСТЕМЫ

Линейная и круговая свертки

2.1.1. Линейная свертка. Обработка сигналов в линейных цифровых системах осуществляется по алгоритмам, являющимися дискретными аналогами интеграла свертки [1]

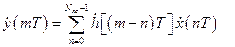
или при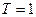

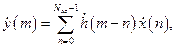(2.1)

где 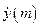– выходной отклик, состоящий из 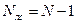отсчетов; 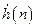– импульсная характеристика линейной системы, состоящая из 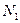отсчетов; 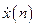– отсчеты входного сигнала, количество которых равно 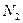; величина 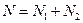; 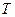– период дискретизации.

Выражение (2.1) для простоты обозначения переменных часто записывают в форме

.

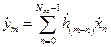Другая форма записи выражения (2.1) имеет вид

,

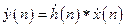или в виде

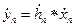, (2.2)

где знак 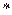– обозначает операцию свертки.

Линейная свертка (2.1) или (2.2) также носит название апериодической и описывает работу линейных цифровых систем, работающих в режиме «скользящее» окно [1].

Пример 2. Пусть имеем последовательность 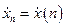, состоящую из 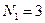отсчетов в виде

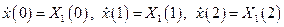. (2.3)

Пусть также имеется последовательность 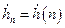, состоящая из 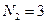отсчетов в виде

.

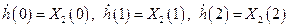Количество выходных отсчетов 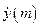будет равно величине

.

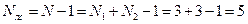Используя выражение (2.1) вычислим линейную свертку для соответствующих временных значений.

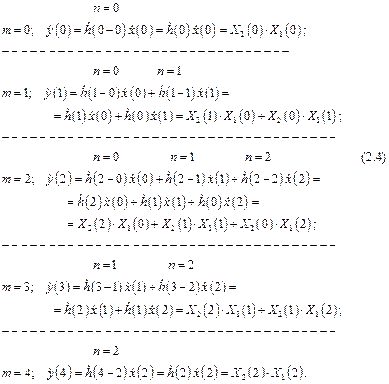
2.1.2. Круговая свертка. Часто та или иная последовательность отсчетов носит периодический характер с периодом 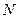отсчетов. Например, отсчеты в частотной области выборочного спектра входного сигнала с периодом 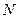отсчетов, отсчеты в частотной области амплитудно-частотной характеристики (АЧХ) цифровой линейной цепи с периодом 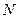отсчетов. Очевидно, что выходной результирующий спектр, являющийся результатом произведения соответствующих отсчетов спектра входного сигнала и АЧХ друг на друга, тоже будет периодическим с периодом 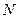отсчетов.

Обратное преобразование Фурье выходного спектра с периодом 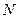отсчетов также будет периодическим во временной области с периодом 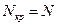отсчетов.

Выражение во временной области для круговой свертки периодического выходного результирующего спектра с периодом 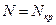отсчетов будет иметь вид

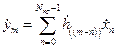. (2.5)

Выражение (2.4) может быть записано в виде

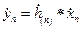. (2.6)

В выражениях (2.5) и (2.6) индексы в круглых скобках при значениях 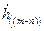и 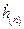обозначают, что они берутся по модулю 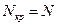отсчетов.

Например, если модуль 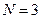, то

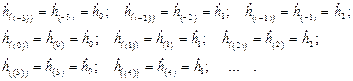
Количество отсчетов во времени круговой свертки, как видно из (2.5), равно количеству отсчетов в частотной области, в то время как количество отсчетов линейной свертки в (2.1), зависит от количества отсчетов используемых при расчетах реализаций (импульсной характеристики и входного процесса), ее образующих, минус один отсчет.

Пример 3. Пусть имеем последовательность 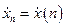, состоящую из 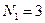отсчетов в виде (2.3)

.

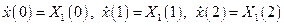Пусть также имеется последовательность 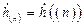, состоящая из 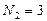отсчетов в виде

.

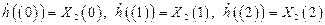Количество различных выходных отсчетов 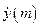для круговой свертки будет равно величине .

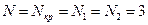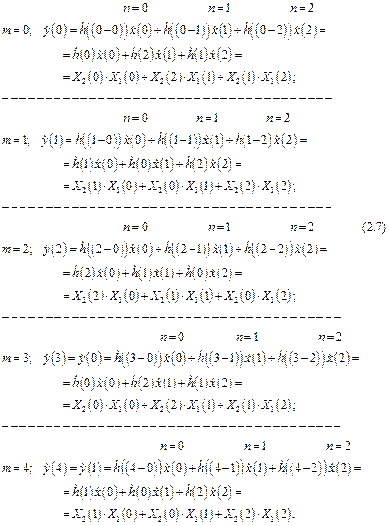
В выражении (2.7) видно, что выходные отсчеты для круговой свертки повторяются с периодом .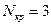

2.1.3. Пример 4. Вычислить и изобразить на рисунке линейную и круговую свертки для двух конечных последовательностей длительностью по три отсчета каждая. Здесь полагается, что величина периода дискретизации .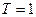

Первая конечная последовательность

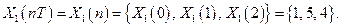
Вторая конечная последовательность

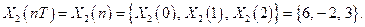
Линейная свертка. Подставляя в (2.4) численные значения получаем следующие результаты

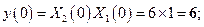
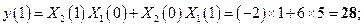
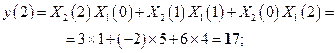
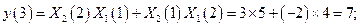
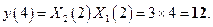
Следовательно, отсчеты линейной свертки имеют вид

.

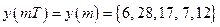На рис. 1 изображены отсчеты линейной свертки.

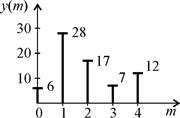Рис. 1. Отсчеты линейной свертки

Круговая свертка. Подставляя в (2.7) численные значения получаем следующие результаты.

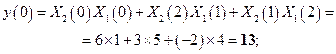
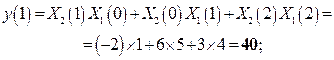
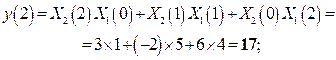
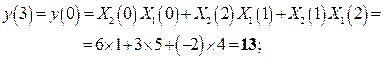
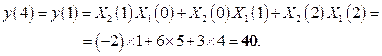
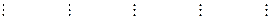
Далее процесс расчета повторяется.

Следовательно, отсчеты круговой свертки имеют вид

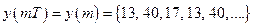
и они периодически повторяются с периодом .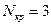

На рис. 2 изображены отсчеты круговой свертки.

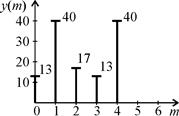Рис. 2. Отсчеты круговой свертки

Видно, что отсчет 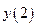линейной свертки численно совпадает с отсчетом 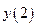круговой свертки. Это используется при вычислении спектров с использованием алгоритмов быстрого расчета коэффициентов Фурье.

Аналогичным образом решаются все задачи в п.10.1.4. в [2].

2.2. Дискретное преобразование Фурье

Вычисление отсчетов дискретного преобразования Фурье 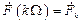осуществляется в соответствии с выражением

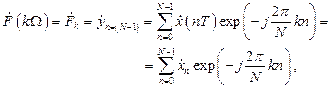(2.8)

где 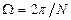(рад) – бин, т.е. минимальный фазовый сдвиг от отсчета к отсчету за интервал времени, равный периоду дискретизации 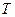, который полагается равным единице; 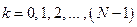– номера частотных составляющих, количество которых равно величине 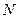; 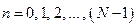– номера отсчетов обрабатываемого сигнала 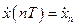во времени; 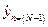– выходной отклик в момент времени 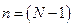, величина которого равна значению коэффициента Фурье.

Раскрывая выражение (2.8), получим формулы для расчета каждого коэффициента Фурье, которые примут вид

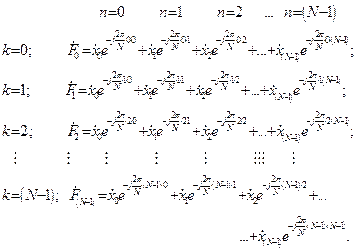(2.9)

В том случае, если

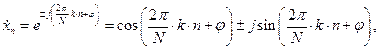
где 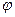(рад) – начальная фаза, то видно, что сигнал представляет собой отсчеты комплексной синусоиды, амплитуда которой равна единице, т.е. огибающая сигнала имеет прямоугольную форму. Известно, что сигнал с прямоугольной огибающей имеет форму спектра в виде 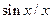. При этом расположение спектра на частотной оси, форма которого 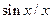, определяется частотой заполнения сигнала.

Пример 5. Вычислить дискретное преобразование Фурье сигнала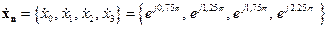

согласно выражения (2.8) для значени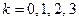й и 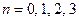. Величина 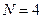. Изобразить на рисунке полученный спектр (в виде сплошных линий) и его огибающую (пунктиром).

Для упрощения расчетов сделаем ряд преобразований. Учтем, что на форму огибающей спектра не оказывает влияние величина начальной фазы. В рассматриваемом случае 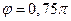(рад). Тогда сигнал может быть переписан в виде

.

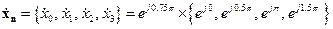Очевидно, что результат не изменится, если вместо сигнала 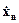рассматривать сигнал

.

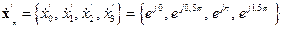Также учтем, что 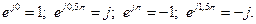Воспользуемся выражениями (2.9) и определим величину бина для данной задачи, которая будет 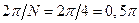(рад).

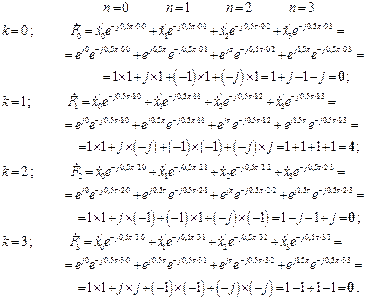
На рис. 3 изображен полученный амплитудный спектр 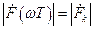в виде сплошных линий, что соответствует отклику соответствующих частотно-избирательных цепей, вычисляющих дискретное преобразование Фурье, а пунктирными линиями – его огибающая.

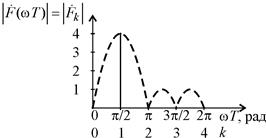Рис. 3. Рассчитанный спектр сигнала и его огибающая

Видно, что центральная частота сигнала расположена на частоте, которая составляет одну четвертую часть частоты дискретизации.

Аналогичным образом решаются все задачи в п.10.1.5. в [2].

2.3. Связь Z-преобразования с преобразованием Лапласа

Известно, что изображение по Лапласу временных процессов, а также передаточных функций линейных цепей отображается в виде 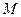точек в р-плоскости в ее левой части. При дискретизации происходит «размножение» этих точек с периодом 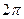. Это может быть отображено на р-плоскости в виде бесконечного множества, повторяющихся с периодом 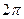, точек.

Для сохранения прежнего количества 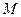точек для описания дискретной функции, которую получают путем дискретизации аналоговой временной функции, описываемой 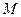точками, вводят новую переменную 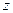, расположенную в Z-плоскости.

Переменная 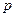в р-плоскости связана с переменной 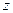в Z-плоскости соотношением [1]

,

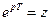где 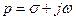; 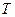– период дискретизации (с).

Из рассмотрения величины 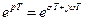видно, что она состоит из модуля, равного величине 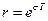и показывающего, как изменяется амплитуда функции от отсчета к отсчету, и величины 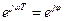, показывающей, как изменяется фазовый угол этой амплитуды от отсчета к отсчету.

Очевидно, необходимо чтобы амплитуда сигнала уменьшалась от отсчета к отсчету. Это соответствует тому, что амплитуда процесса во времени постепенно «затухает», как происходит во всех реальных линейных системах, либо амплитуда не изменялась бы, что соответствует процессу на выходе «идеального» генератора.

Для этого необходимо, чтобы величина .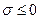

Если величина 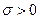, то в этом случае амплитуда процесса будет нарастать от отсчета к отсчету, что противоречит работе реальных пассивных линейных систем.

При 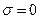, т.е. тогда, когда величина 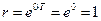, переменная 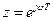. Величина обратная переменной 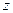определяется в виде 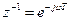и описывает цифровой элемент задержки, осуществляющий задержку отсчета на период дискретизации .

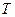Таким образом, каждая точка на р-плоскости описывается в декартовой системе координат. При этом по оси абсцисс, обозначаемой действительной величиной 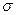, откладывается величина 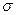, а по оси ординат, обозначаемой мнимой величиной 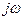, откладывается величина 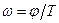(рад/с).

На Z-плоскости соответствующая точка описывается в полярной системе координат. При этом фазовый угол 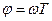(рад) откладывается от оси абсцисс. Расстояние от точки, из которой начинается ось абсцисс, до местонахождения искомой точки по радиусу под углом 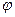(рад), будет равно величине .

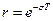Пример 6. По заданным параметрам, полагая 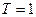(с), вычислить значения и нарисовать на рисунке взаимно-однозначное положение точек на р- и Z-плоскостях. Объяснить, почему значение 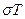задано отрицательной величиной.

Пусть 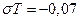, а 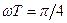, т.е. .

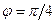Эти две величины определяют положение соответствующей точки на р-плоскости в декартовой системе координат в соответствии с выражениями:

по оси абсцисс, обозначаемой 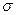, величина ;

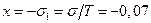по оси ординат, обозначаемой 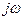, величина 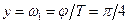(рад/с).

Положение точки на Z-плоскости в полярной системе координат определится в соответствии с выражениями:

угол равен 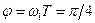(рад);

величина радиуса .

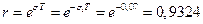На рис. 4 изображено положение рассмотренной точки 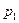на р-плоскости, а на рис. 5 – показан ее переход в положение 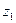на Z-плоскости.

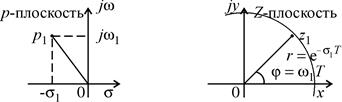Рис. 4. Положение точки на р-плоскости	Рис. 5. Положение точки на Z-плоскости

Поскольку положение точек на р-плоскости периодически повторяется, то, следовательно, на Z-плоскости эти точки накладываются друг на друга.

Аналогичным образом решаются все задачи в п.10.1.6. в [2].

Элементарных ячеек

2.4.1. Как известно, основной характеристикой линейной цифровой частотно-избирательной цепи, которая также называется цифровым фильтром (ЦФ), является ее передаточная функция , которая представима в виде

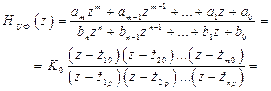
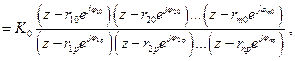(2.10)

где 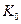– коэффициент пропорциональности; 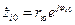– нули; 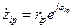– полюса; 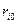и 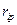– модули 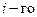нуля и 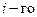полюса; 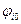и 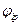– фазовые углы 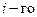нуля и 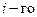полюса; 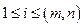; 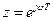– независимая переменная; 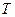– период дискретизации, определяемый из условия выполнения теоремы Котельникова; 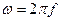(рад/с) – круговая частота; 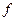(Гц) – частота. Для физически реализуемых систем порядки полиномов числителя и знаменателя должны быть .

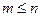Выражение (2.10) при 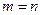можно представить в виде

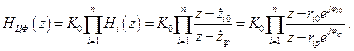(2.11)

Отношение полиномов первого порядка в (2.11) описывает передаточную функцию 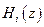цифровой комплексной ячейки первого порядка. Тогда, опуская индекс 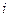, можно записать ее передаточную функцию в виде

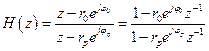. (2.12)

Числитель в выражении (2.12) описывает передаточную функцию цифровой элементарной нерекурсивной ячейки, а знаменатель – рекурсивной.

В том случае, когда в (2.11) полюса и нули являются попарно комплексно-сопряженными, передаточная функция описывает соответственно рекурсивную и нерекурсивную биквадратные ячейки, которые имеют второй порядок каждая.

Передаточная функция элементарной биквадратной ячейки имеет вид

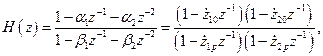(2.13)

где ; ; ; ; .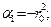

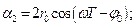
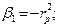
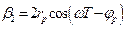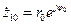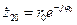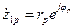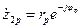Видно, что биквадратная ячейка, описываемая выражением (2.13), представляет собой каскадное соединение элементарных ячеек первого порядка с комплексно-сопряженными нулями и полюсами.

2.4.2. Нерекурсивная ячейка первого порядка.

2.4.2.1. Существуют нерекурсивные ячейки двух видов. Передаточная функция нерекурсивной ячейки первого вида, полученная непосредственно из (2.12), будет

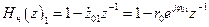. (2.14)

Импульсная характеристика (ИХ) этой ячейки определяется следующим образом.

Перепишем выражение (2.14) в виде

.

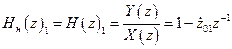Тогда

.

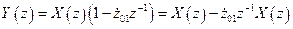Выполняя обратное Z-преобразование над последним выражением, получим дискретную форму записи в виде [1]

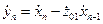. (2.15)

Поскольку работа любой цепи начинается в момент времени 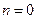, то величина .

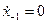Тогда выходной отклик 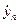из выражения (2.15) для последовательности входных данных 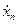в каждый 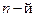момент времени будет

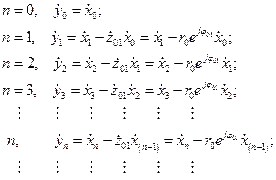(2.16)

Для определения ИХ любой цепи используется входная импульсная последовательность в виде цифровой « 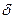-функции», которая представляет собой единичную функцию 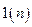в момент времени 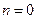, т.е. 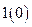, длительностью 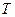(с).

Тогда, при 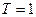, входные данные будут иметь вид

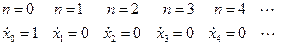(2.17)

Подавая входные отсчеты (2.17) в (2.16) получим ИХ нерекурсивной комплексной ячейки первого вида

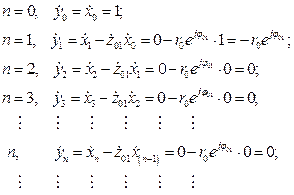
Таким образом, ИХ нерекурсивной ячейки первого вида в соответствующие моменты времени 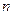будет

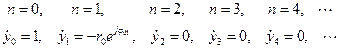
Определим амплитудно-частотную характеристику (АЧХ) нерекурсивной ячейки. Для этого подставим в (2.14) величины 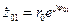и 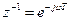. В результате получим

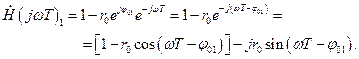
Для нахождения АЧХ необходимо найти модуль последнего выражения. По определению, модуль комплексного числа .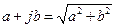

Тогда будем иметь