Экспоненциальное распределение

Плотность вероятности , где , .

Функция распределения

Вероятность безотказной работы

Интенсивность отказов .

Соотношения между моментами и параметром распределения "λ":

Для среднего времени наработки до отказа .

Для дисперсии и среднеквадратичного отклонения ; .

Для коэффициентов асимметрии и эксцесса ; .

Для медианы . Коэффициент вариации .

Гамма-распределение

Плотность вероятности наработки до отказа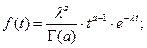

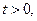
где 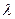— параметр масштаба ( 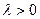), 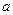— параметр формы ( 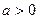), 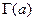— гамма-функция или эйлеров интеграл второго рода 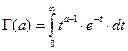или

.

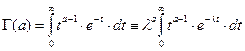Аналитического выражения для функции распределения наработки на отказ 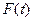не существует (аналитическое выражения для нее существует только для целых положительных значений параметра 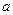; см. ниже распределение Эрланга).

Известны формулы связи моментов с параметрами "a" и "λ" гамма-распределения:

; ; ; ; .

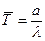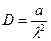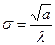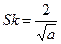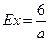Коэффициент вариации при этом 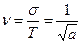. Мода: 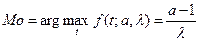для значений 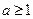. Квантиль 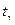находится из уравнени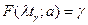я для 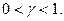Точка перегиба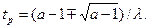

Начальные моменты таковы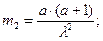

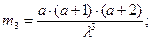
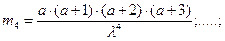
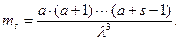
В задачах обработки статистических экспериментальных данных потребуются выражения и оценки численных значений производной 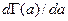и функции 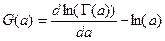или в развернутом виде .

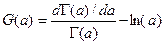Нетрудно показать, что = ,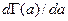

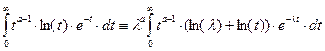а функция примет вид .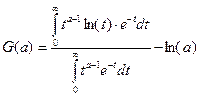

При 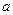— целом ( 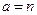) функция 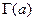принимает значения 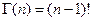, то есть,

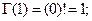
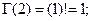
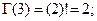
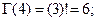
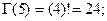... и т.д. Таким образом, гамма-функция Эйлера - это распространение функции или операции «факториал» на случай нецелых чисел, в том числе и отрицательных.

Табличные значения функции 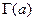в справочниках ограничены значениями аргумента "a", принадлежащими интервалу .

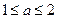Значения гамма-функции для 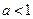, но при этом ... ,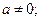

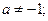
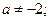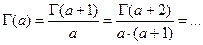При больших значениях a ( 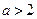) по формуле 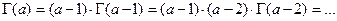, которые следуют из функционального уравнения Эйлера .

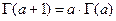Примеры:

; ;

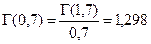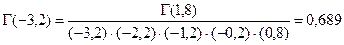Полезные соотношения и значения гамма-функции:

; .

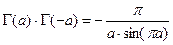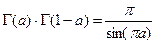Функция распределения времени наработки до отказа, как отмечалось выше, не имеет аналитического выражения. В общем виде она может быть представлена таким образом

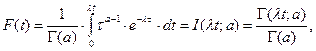
где 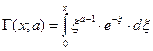— неполная гамма-функция.

пр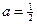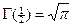и : ; при : ;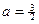

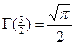Примечание. Из гамма-распределения «вытекают»:

при 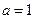— экспоненциальное распределение;

при 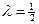и a, кратном 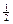, будем иметь χ²-распределение (при этом 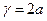— число степеней свободы);

при a — целом: a = 1; 2; ... ; k; ... — распределение Эрланга.

Существенное уменьшение вычислительных трудностей может быть достигнуто применением асимптотических разложений (аппроксимационных формул) Стирлинга:

.

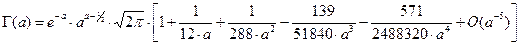Ряд Стирлинга полезен для больших 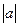. Для действительных положительных a абсолютные величины ошибки меньше, чем абсолютная величина последнего из взятых членов.

Другие полезные аппроксимации Стирлинга: 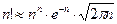при .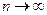

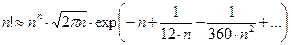. Известно важное неравенство:

< < .

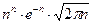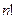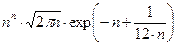Распределение Эрланга

Плотность распределения наработки до отказа:

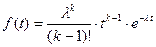
для 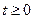; ; 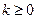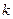— целое.

Функция распределения времени наработки до отказа:

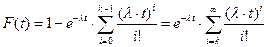
Вероятность безотказной работы:

.

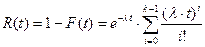Интенсивность отказов системы в целом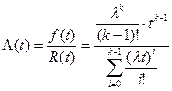

Соотношения между моментами и параметрами распределения определяются как и у гамма-распреденения, но с заменой параметр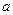а на .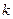

Распределение Эрланга порядка k описывает распределение случайной величины 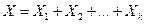как суммы k штук независимых случайных величин, каждая из которых распределена по показательному (экспоненциальному) закону с параметром λ.

Распределению Эрланга удовлетворяет время наработки до отказа резервированной системы с включением «холодного» резерва по способу замещения при условии, что наработка до отказа включенного элемента подчинена экспоненциальному закону. При этом 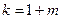, где m — число резервных элементов. Из соотношения 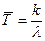вытекает свойство структур с «холодным» резервом – средняя наработка системы до отказа линейно возрастает от числа резервных элементов.