Программы и результаты решения конкретной задачи обработки статистических данных

5.1. Постановка задачи

В качестве исходными данными для практической отработки предложенных алгоритмов являются конкретная выборка объемом из 50-ти наблюдений 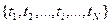, где N=50, принадлежащая некоторой генеральной совокупности с неизвестным законом распределения случайной величины, который подлежит «разгадыванию» среди множества стандартных распределений.

Наиболее важные стандартные распределения и соотношения теоретических моментов с параметрами распределения приведены в справочном Приложении 1.

Там же приведены соответствующие преобразования для применения метода « вероятностной бумаги».

5.2. Расчет первых четырех выборочных моментов и построение эмпирической функции распределения

Рассмотрим полную выборку из 50 элементов(N=50), сгенерированную для генеральной совокупности, описываемой (для определенности) распределением Вейбулла с параметрами 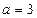и :

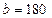140;223;58;113;222;192;168;225;182;239;149;53;126;66;242;165;145;159;205;196;130;122; 143;244;78;244;160;198;175;76;162;147;211;225;203;153;92;117;133;109;142;128;132;202 156;126;192;264;197;118.

Результаты расчета первых четырех начальных и центральных моментов, произведенных по выше приведенным формулам, таковы.

Начальные моменты:

.

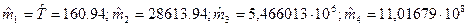Центральные моменты:

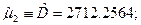
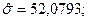
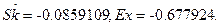
Центральные несмещенные моменты:

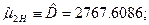
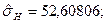
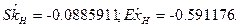
Приведем несколько программ расчета моментов в среде ПК «МВТУ»:

Программа 1.

t=time;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

N=50;

{Расчет начальных моментов }

m1=(t1+t2+t3+t4+t5+t6+t7+t8+t9+t10+t11+t12+t13+t14+t15+t16+t17+t18+t19+t20+

t21+t22+t23+t24+t25+t26+t27+t28+t29+t30+t31+t32+t33+t34+t35+t36+t37+t38+t39+

t40+t41+t42+t43+t44+t45+t46+t47+t48+t49+t50)/N;

m2=(t1^2+t2^2+t3^2+t4^2+t5^2+t6^2+t7^2+t8^2+t9^2+t10^2+t11^2+t12^2

+t13^2+t14^2+t15^2+t16^2+t17^2+t18^2+t19^2+t20^2+t21^2+t22^2+t23^2+t24^2

+t25^2+t26^2+t27^2+t28^2+t29^2+t30^2+t31^2+t32^2+t33^2+t34^2+t35^2+t36^2

+t37^2+t38^2+t39^2+t40^2+t41^2+t42^2+t43^2+t44^2+t45^2+t46^2+t47^2+t48^2

+t49^2+t50^2)/N;

m3=(t1^3+t2^3+t3^3+t4^3+t5^3+t6^3+t7^3+t8^3+t9^3+t10^3+t11^3+t12^3

+t13^3+t14^3+t15^3+t16^3+t17^3+t18^3+t19^3+t20^3+t21^3+t22^3+t23^3+t24^3

+t25^3+t26^3+t27^3+t28^3+t29^3+t30^3+t31^3+t32^3+t33^3+t34^3+t35^3+t36^3

+t37^3+t38^3+t39^3+t40^3+t41^3+t42^3+t43^3+t44^3+t45^3+t46^3+t47^3+t48^3

+t49^3+t50^3)/N;

m4=(t1^4+t2^4+t3^4+t4^4+t5^4+t6^4+t7^4+t8^4+t9^4+t10^4+t11^4+t12^4

+t13^4+t14^4+t15^4+t16^4+t17^4+t18^4+t19^4+t20^4+t21^4+t22^4+t23^4+t24^4

+t25^4+t26^4+t27^4+t28^4+t29^4+t30^4+t31^4+t32^4+t33^4+t34^4+t35^4+t36^4

+t37^4+t38^4+t39^4+t40^4+t41^4+t42^4+t43^4+t44^4+t45^4+t46^4+t47^4+t48^4

+t49^4+t50^4)/N;

{Расчет центральных моментов по формулам теоретической связи}

Mu2=m2-m1^2;

Mu3=m3-3*m1*m2+2*m1^3;

Sk=Mu3/(sqrt(Mu2))^3;

Mu4=m4-4*m1*m3+6*m2*(m1^2)-3*m1^4;

Ex=(Mu4/(sqrt(Mu2))^4)-3;

sko=sqrt(Mu2);

output m1,m2,m3,m4,Mu2,Mu3,Sk,Mu4,Ex,sko;

Для сравнения произведем расчет первых четырех центральных моментов непосредственно по выборке по следующей программе.

Программа 2.

t=time;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

N=50;

{T=(t1+t2+t3+t4+t5+t6+t7+t8+t9+t10+t11+t12+t13+t14+t15+t16+t17+t18+t19+t20+

t21+t22+t23+t24+t25+t26+t27+t28+t29+t30+t31+t32+t33+t34+t35+t36+t37+t38+t39+

t40+t41+t42+t43+t44+t45+t46+t47+t48+t49+t50)/N;}

T=160.94;

D=((t1-T)^2+(t2-T)^2+(t3-T)^2+(t4-T)^2+(t5-T)^2+(t6-T)^2+(t7-T)^2+(t8-T)^2+

(t9-T)^2+(t10-T)^2+(t11-T)^2+(t12-T)^2+(t13-T)^2+(t14-T)^2+(t15-T)^2+(t16-T)^2+

(t17-T)^2+(t18-T)^2+(t19-T)^2+(t20-T)^2+(t21-T)^2+(t22-T)^2+(t23-T)^2+(t24-T)^2+

(t25-T)^2+(t26-T)^2+(t27-T)^2+(t28-T)^2+(t29-T)^2+(t30-T)^2+(t31-T)^2+(t32-T)^2+

(t33-T)^2+(t34-T)^2+(t35-T)^2+(t36-T)^2+(t37-T)^2+(t38-T)^2+(t39-T)^2+

(t40-T)^2+(t41-T)^2+(t42-T)^2+(t43-T)^2+(t44-T)^2+(t45-T)^2+(t46-T)^2+

(t47-T)^2+(t48-T)^2+(t49-T)^2+(t50-T)^2)/N;

Sko=sqrt(D);

Skos= (((t1-T)^3+(t2-T)^3+(t3-T)^3+(t4-T)^3+(t5-T)^3+(t6-T)^3+(t7-T)^3+(t8-T)^3+

(t9-T)^3+(t10-T)^3+(t11-T)^3+(t12-T)^3+(t13-T)^3+(t14-T)^3+(t15-T)^3+(t16-T)^3+

(t17-T)^3+(t18-T)^3+(t19-T)^3+(t20-T)^3+(t21-T)^3+(t22-T)^3+(t23-T)^3+(t24-T)^3+

(t25-T)^3+(t26-T)^3+(t27-T)^3+(t28-T)^3+(t29-T)^3+(t30-T)^3+(t31-T)^3+(t32-T)^3+

(t33-T)^3+(t34-T)^3+(t35-T)^3+(t36-T)^3+(t37-T)^3+(t38-T)^3+(t39-T)^3+

(t40-T)^3+(t41-T)^3+(t42-T)^3+(t43-T)^3+(t44-T)^3+(t45-T)^3+(t46-T)^3+

(t47-T)^3+(t48-T)^3+(t49-T)^3+(t50-T)^3)/N)/Sko^3;

Exc=((((t1-T)^4+(t2-T)^4+(t3-T)^4+(t4-T)^4+(t5-T)^4+(t6-T)^4+(t7-T)^4+(t8-T)^4+

(t9-T)^4+(t10-T)^4+(t11-T)^4+(t12-T)^4+(t13-T)^4+(t14-T)^4+(t15-T)^4+(t16-T)^4+

(t17-T)^4+(t18-T)^4+(t19-T)^4+(t20-T)^4+(t21-T)^4+(t22-T)^4+(t23-T)^4+(t24-T)^4+

(t25-T)^4+(t26-T)^4+(t27-T)^4+(t28-T)^4+(t29-T)^4+(t30-T)^4+(t31-T)^4+(t32-T)^4+

(t33-T)^4+(t34-T)^4+(t35-T)^4+(t36-T)^4+(t37-T)^4+(t38-T)^4+(t39-T)^4+

(t40-T)^4+(t41-T)^4+(t42-T)^4+(t43-T)^4+(t44-T)^4+(t45-T)^4+(t46-T)^4+

(t47-T)^4+(t48-T)^4+(t49-T)^4+(t50-T)^4)/N)/Sko^4)-3;

output {T} D,Sko,Skos,Exc;

Результаты расчетов для их сравнения сведем в таблицу.

Таблица. Оценки центральных моментов

Метод расчета	Дисперсия	с.к.о	Skewness	Excess
По найденным начальным	2712.2564	52.07933	-0.0859109	-0.677924
По выборке	2712.2564	52.07933	-0.0859109	-0.677924
Несмещенные оценки	2767.6086	52.60806	-0.0885911	-0.591176

Как видно из таблицы результаты расчета центральных моментов на основе найденных начальных моментов по теоретически связующим их формулам совпадают с прямым расчетом по выборке. Для дальнейших расчетов мы примем несмещенные оценки, полученные при расчете непосредственно по выборке.

Уже по полученным оценкам могут быть сразу исключены из рассмотрения показательный и нормальный законы. Поиски необходимо вести среди распределений с отрицательной ассиметрией формы плотности вероятности.

Среди них подозрение падает, в частности на законы Вейбулла, гамма-распределение, логнормальный закон распределения и может быть на некоторые другие (см. Приложение 1).

Полученные несмещенные точечные оценки моментов используем в дальнейшем при проведении оценок параметров предполагаемых распределений методами моментов и максимального правдоподобия.

Представим в графическом виде эмпирическую функцию распределения 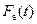как ступенчатой функции от аргумента с использованием средств ПК «МВТУ».

Программа 3.

t=time;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);

x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);

x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);

x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);

x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);

x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);

x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);

x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);

x49=step(t49,0,1);x50=step(t50,0,1);

F=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

output F;

При решение задачи использован адаптивный неявный метод с минимальным и максимальным шагами расчета 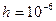и 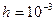соответственно и заданной точностью 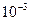. Полученный график приведен на рис. 5.1.

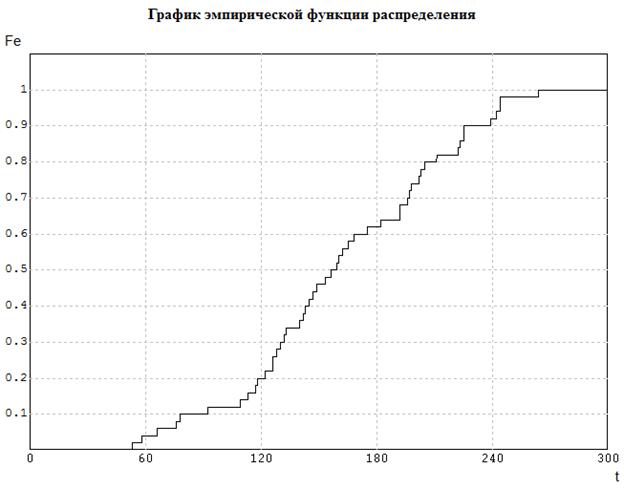
Рис. 5.1 – График эмпирической функции распределения

Наглядный вид эмпирической функции распределения и количественные значения вычисленных моментов позволяют уточнить или сузить число выдвигаемых гипотез о предполагаемых законах распределения случайной исследуемой величины, оговорив все основания для этого.

Выбор гипотез о предполагаемых законах распределения случайной величины в данном случае должен осуществляться, очевидно, из числа следующих стандартных:

- логнормальное распределение;

- гамма-распределение, включая распределение Эрланга с целочисленным параметром формы;

- распределение Вейбулла;

- распределение минимального значения;

- распределение максимального значения;

- распределение Релея.

5.3. Расчет параметров предполагаемых теоретических распределений методом моментов

На этом этапе для оценок параметров распределений, выдвинутых в качестве гипотез, будем использовать метод моментов, по крайней мере, как наиболее простой и как «прикидочный».

Для решения соответствующих достаточно сложных нелинейных систем алгебраических уравнений будем отрабатывать одновременно и эффективные алгоритмы и вычислительные процедуры или разработать собственные более эффективные. Проделаем здесь такую работу для гамма-распределения и для распределения Вейбулла.

Для гамма-распределения с параметрами "a" и "λ" необходимые связи между моментами и параметрами распределения таковы:

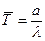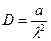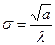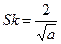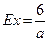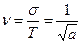; ; ; ; ; - коэффициент вариации.

Рассчитав оценку коэффициента вариации 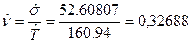, из уравнения

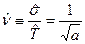находим оценку параметр формы 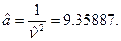И сразу же из первого уравнения 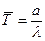находим оценку параметра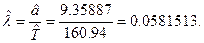

В результате для гипотезы о гамма-распределении запишем аналитическое выражение для плотности вероятности

.

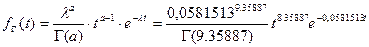Значение гамма-функции Эйлера для параметра 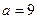будем рассчитывать по формуле Стирлинга

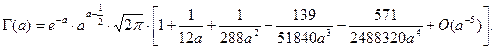
Для получения графика функции гамма распределения при оцененных параметрах будем интегрировать дифференциальное уравнение вида

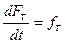
при начальном условии 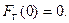Полученное решение 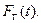наложим на график эмпирической функции распределения 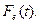(см. рис. 5.2).

Приведем текст программы выполнения расчетов в ПК «МВТУ»:

Программа 4.

t=time;

init F=0,D=0;

a=9.36;

l=0.058;

{Q=1+(1/12)*a^(-1)+(1/288)*a^(-2)-(139/51840)*a^(-3)-

(571/2488320)*a^(-4);

Ã=exp(-a)*a^(a-0.5)*sqrt(2*pi)*Q;}

Ã=87577.00612;

f=(l^a)*((t)^(a-1))*(exp(-l*t))/Ã;

F'=f;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

Fe=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

y=abs(Fe-F);

D'=10*(1+sign(y-D));

output Fe,F,f,y,D;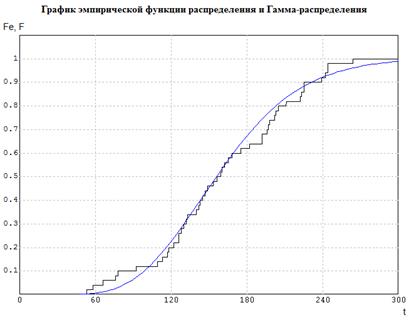

Рис. 5.2 – Аппроксимация эмпирической функции распределения гамма-распределением с параметрами, найденными методом МОМЕНТОВ

Из рисунка следует, что «на глаз» аппроксимация эмпирической (ступенчатой) функции распределения гамма-распределением достаточно приемлема. Однако следует провести более углубленный анализ.

Рассмотрев график плотности вероятности аппроксимирующего Гамма-распределения (см. рис. 5.3), видим, что f(t) практически симметрично, но в то же время заметно, что имеется положительная асимметрия, т.е. 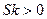, хотя точечные оценки выявили отрицательность коэффициента асимметрии.

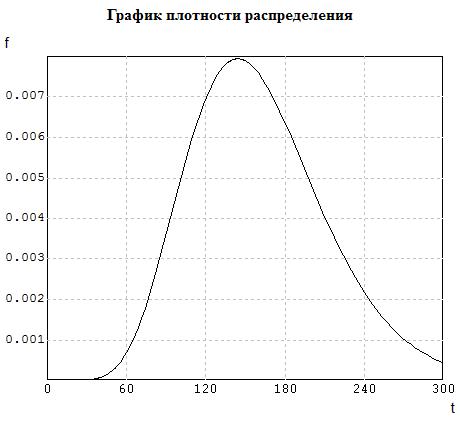
Рис. 5.3 – График плотности вероятности распределения гамма-распределением с параметрами, найденными методом МОМЕНТОВ

Действительно, в методе МОМЕНТОВ не используется информация о точечных эмпирических оценках 3-го и 4-го центральных моментов, несмещенные значения которых, как было показано выше 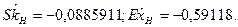Рассчитанные же значения этих моментов для полученного нами аппроксимирующего гамма-распределения 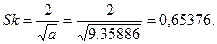; 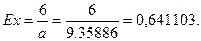, что отличается не только и не столько по величине, сколько по знаку.

В связи с этим гипотеза о принадлежности выборки гамма-распределению оказалась, по крайней мере, сомнительной.

Приведем также результаты расчета (см. ту же программу) выборочной статистики Колмогорова .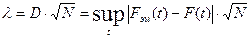

Для расчета использовались следующая модель:

- вычисляется изменения модуля «рассогласования» эмпирического и теоретического распределений 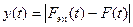во времени (см. рис.4);

- интегрируется дифференциальное уравнение Y'=10*(1+sign(y-Y)), обеспечивающее фиксацию максимального значения рассогласования на интервале (0, 300).

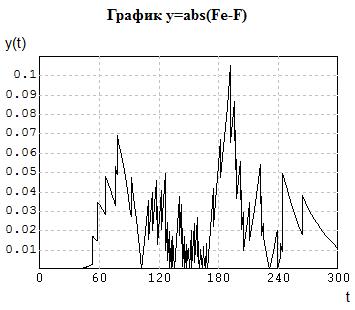
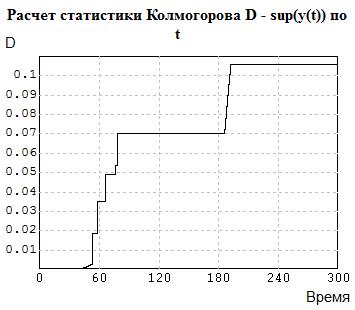
Рис. 5.4. Расчет статистики Колмогорова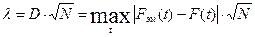

Нами получена оценка D=0.105701. Тогда 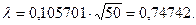И при принятых значениях 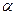=0,05 и 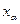=1,358 имеем 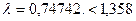. То есть нет оснований для отрицания гипотезы о гамма-распределении.

Обратимся к распределению Вейбулла с параметрами "a" и "b", которые оценим методом МОМЕНТОВ. Необходимые для решения такой задачи связи между первыми двумя моментами и параметрами распределения таковы:

, , .

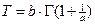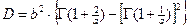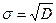Выражая из первого соотношения 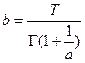и подставляя его во второе соотношение, получим алгебраическое уравнение относительно параметра "a"

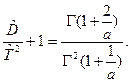
В нашем примере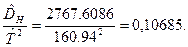

И уравнение приобретает окончательный вид

.

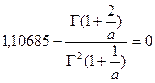Учитывая свойство строгой вогнутости функции 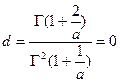, что показано на рисунке, будем искать решение путем интегрирования уравнения

,

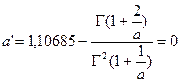в котором правая часть представляется «невязкой»

.

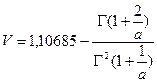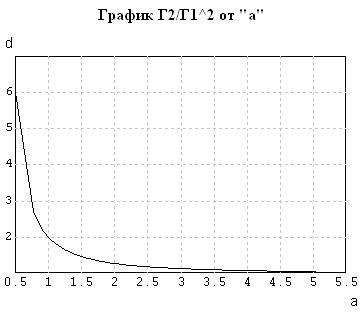
Рис. 5.5

Введенная «отрицательная обратная связь» по «а» обеспечивает при некоторых (пусть произвольных) начальных условиях, например a=0.5, стремление невязки к нулю и тем самым получение численного решения исходного алгебраического уравнения. Возможна и «релейная обратная связь», при которой в точке решения будет иметь место «скользящий режим». Приведем программу для решения этого уравнения.

Программа 5.

t=time;

init a=0.5;

a1=1+1/a;

a2=1+2/a;

Q1=1+(1/12)*a1^(-1)+(1/288)*a1^(-2)-(139/51840)*a1^(-3)-

-(571/2488320)*a1^(-4);

Ã1=exp(-a1)*a1^(a1-0.5)*sqrt(2*pi)*Q1;

Q2=1+(1/12)*a2^(-1)+(1/288)*a2^(-2)-(139/51840)*a2^(-3)-

-(571/2488320)*a2^(-4);

Ã2=exp(-a2)*a2^(a2-0.5)*sqrt(2*pi)*Q2;

V=1.10685-Ã2/(Ã1^2); {V=-2.13093E-9}

a'=-V;

{ a=3.3765}

Te=160.94;

a3=3.3765;

a4=1+1/a3;

Q11=1+(1/12)*a4^(-1)+(1/288)*a4^(-2)-(139/51840)*a4^(-3)-

-(571/2488320)*a4^(-4);

Ã11=exp(-a4)*a4^(a4-0.5)*sqrt(2*pi)*Q1;

b=Te/Ã11;

{b=179.209}

output a,V,b;

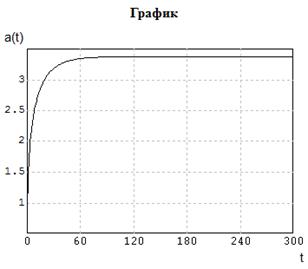
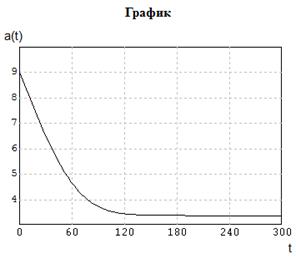
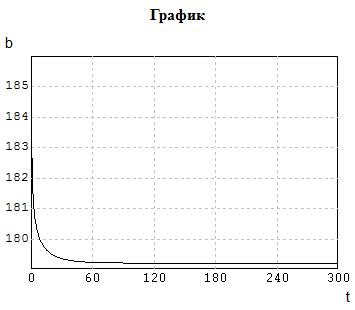
Рис. 5.6. Расчет параметров a и b при различных начальных условиях

Найденные значения параметров распределения Вейбулла таковы «a»=3.3765, «b»=179.209.

После оценки параметров теоретического закона выполним расчеты функций распределения с нанесением (наложением) их графиков на график эмпирической функции распределения 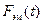, а также рассчитаем все 4 момента, построим для полученного теоретического распределения плотности и интенсивности опасности (отказов).

Программа 6.

t=time;

init Fw=0,D=0,Mu3=0,Mu4=0,Y=0;

N=50;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

a=3.3765;

b=179.209;

T=160.94;

//Fw=1-exp(-(t/b)^a);

f=(a/b)*((t/b)^(a-1))*exp(-(t/b)^a);

Fw'=f;

D'=((t-T)^2)*f;

Sigma=sqrt(D); {36.9611 }

Mu3'=((t-T)^3)*f;

Sk=Mu3/(36.9611^3); {-2.12974 }

Mu4'=((t-T)^4)*f;

Ex=(Mu4/(36.9611^4))-3; {2.14687 }

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

Fe=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

{Îöåíêà ñòàòèñòèêè Êîëìîãîðîâà}

y=abs(Fe-Fw);

Y'=10*(1+sign(y-Y));

output Fe,Fw,f,Sigma,Sk,Ex,y,Y;

Соответствующие результаты приведены на рис. 5.7 и 5.8.

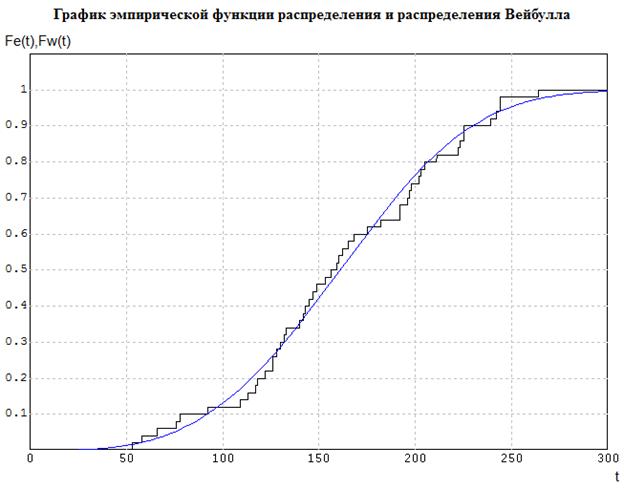
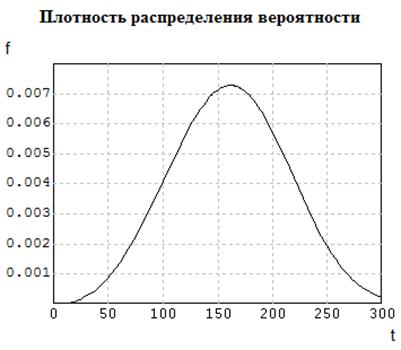
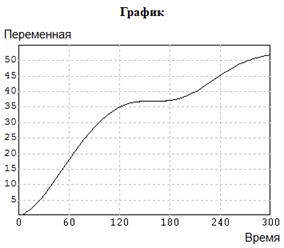
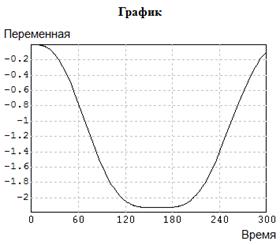
Рис. 5.7. График эмпирической функции распределения и распределения Вейбулла

Результаты оценок для найденных параметров: a=3.3765; b=179.209.

Sigma=52.6646; Sk=-0.127382;

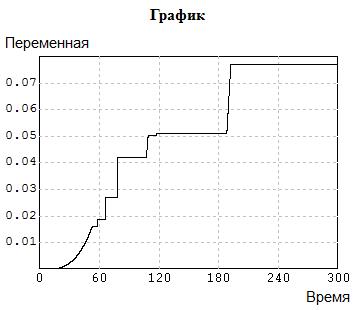
Рис. 5.8 - Оценка состоятельности распределения по критерию Колмогорова.

Нами получена оценка D= 0.0769755. Тогда 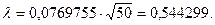И при принятых значениях 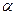=0,05 и 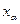=1,358 имеем 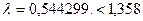. Это даже хуже, чем для Гамма-распределения. И здесь возникаю сомнения. В связи с этим привлечем для решения задачи «разгадывания» распределения метод «Вероятностной бумаги»

Для предполагаемых законов распределения методом «вероятностной бумаги» оценить параметры функций распределения и выявить возможные «ложные» измерения (выбросы) случайной величины с целью их исключения из выборки для получения робастных оценок параметров аналитическими методами. При необходимости следует повторить расчет параметров методом моментов. Программа в ПК МВТУ для распределения Вейбулла такова.

Программа 7.

t=time;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

F=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

Y=ln(0.000001+ln(1/(1-F+0.000000001)));

X=ln(t+10);

output F,Y,X;

Результаты расчетов приведены на рис. 5.9.

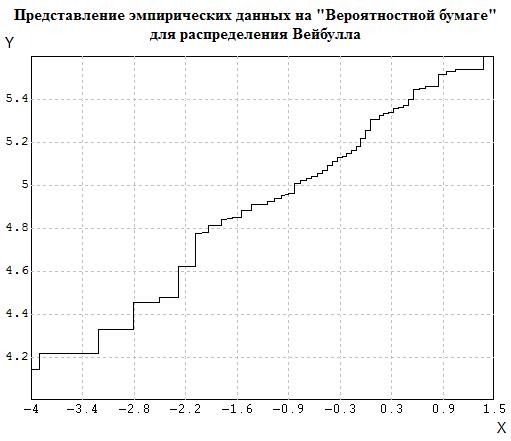
Рис.5.9 - Представление эмпирических данных на «Вероятностной бумаге» для распределения Вейбулла

Из рисунка видно, что экспериментальны точки практически ложатся на прямую. И это делает нас более уверенными в том, что распределение относится к типу распределения Вейбулла.

5.4. Расчет параметров предполагаемых теоретических распределениях методом максимального правдоподобия

Произведем расчеты для гамма-распределения и распределения Вейбулла.

Для гамма-распределения функция правдоподобия, как было показано выше, имеет вид

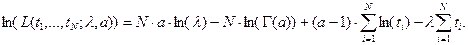
Соответствующее алгебраическое уравнение для получения численной оценки параметра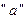

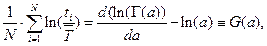
где функция в правой части уравнения (при использовании аппроксимирующей формулы Стирлинга) принимает «раз и навсегда» такое аналитическое выражение

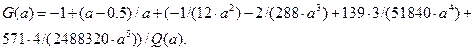
График этой функции, рассчитанный в среде ПК «МВТУ» приведен на рис. 5.10.

Программа8.

t=time;

init a=0.5;

Q=1+(1/12)*a^(-1)+(1/288)*a^(-2)-(139/51840)*a^(-3)- (571/2488320)*a^(-4);

G=-1+(a-0.5)/a+((-1/12)*a^(-2)-(1/288)*2*a^(-3)+(139/51840)*3*a^(-4)+ (571/2488320)*4*a^(-5))/Q;a'=1;

output a,G;

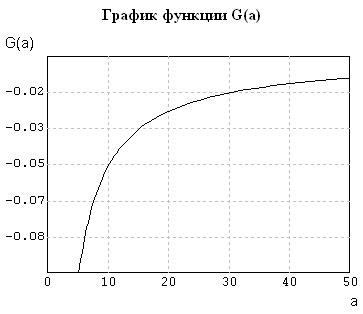
Рис. 5.10 - График «универсальной» функции G(a)

Получив оценку параметра 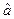, вычисляем затем и оценку параметра 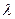по формуле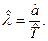

Для решения алгебраического уравнения относительно оценки 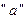необходимо предварительно вычислить значение 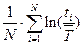по полной выборке при найденной оценке T=160.94

Программа 9 для вычисления константы C.

double temp; double c; int[] vyborka = new int[50] {140,223,58,113,222,192,168,225,182,239,149,53,126,66,242,165,145,159,205,196,130,122,143,244,78,244,160,198,175,76,162,147,211,225,203,153,92,117,133,109,142,128,132,202,156,126,192,264,197,118}; int N; N=vyborka.Length; temp = 0; foreach (double val in vyborka) { temp += Math.Log(val/m1); } c=temp/N; Console.WriteLine(); Console.WriteLine("C={0}", c);

Итак, мы вычислили

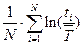
C=-0.062406

и пришли к необходимости решения следующего нелинейного алгебраического уравнения 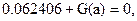где имеет достаточно сложное выражение, но характер ее зависимости от аргумента «а» монотонен, что позволяет нам записать простой алгоритм решения этого уравнения в виде дифференциального уравнения 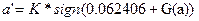при произвольном начальном значении, например при 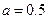, решение которого будет асимптотически приведет к искомому результату.

Программа 10.

t=time;

init a=1;

C=-0.062406;

Q=1+(1/12)*a^(-1)+(1/288)*a^(-2)-(139/51840)*a^(-3)-

-(571/2488320)*a^(-4);

G=-1+(a-0.5)/a+((-1/12)*a^(-2)-(1/288)*2*a^(-3)+(139/51840)*3*a^(-4)+

+(571/2488320)*4*a^(-5))/Q;

a'=0.5*(1-sign(G-C));

output a,Ã,L,G;

Результаты расчета приведены на рис. 5.11. При этом результаты оценки параметров гамма-распределения следующие а=8.17528; 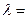0.05078.

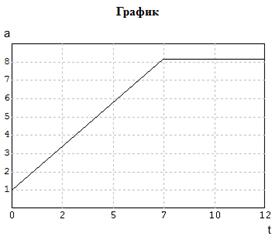
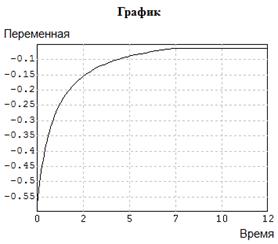
Рис. 5.11 - Графики расчета параметра a и функции G(a)

Для полученных по методу максимального правдоподобия параметров для гамма-распределения рассчитаем график изменения теоретического (аппроксимирующего) распределения и наложим его на эмпирическую функцию распределения и одновременно рассчитаем критерий согласия Колмогорова.

Программа 11.

t=time;

init F=0,Y=0;

a=8.17528;

l=0.05078;

Q=1+(1/12)*a^(-1)+(1/288)*a^(-2)-(139/51840)*a^(-3)-

(571/2488320)*a^(-4);

Ã=exp(-a)*a^(a-0.5)*sqrt(2*pi)*Q;

f=(l^a)*((t)^(a-1))*(exp(-l*t))/Ã;

F'=f;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

Fe=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

y=abs(Fe-F);

Y'=10*(1+sign(y-Y));

output Fe,F,f,y,Y;

Приведем на рисунках 5.12 и 5.13 графики соответствующих функций распределения и плотности вероятности.

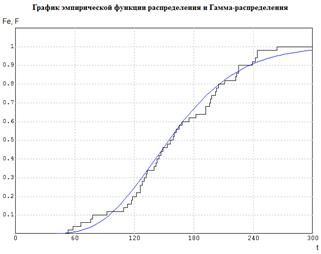
Рис. 5.12 График эмпирической функции распределения и Гамма-распределения

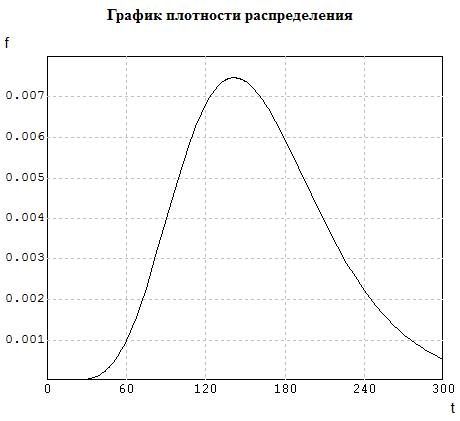
Рис. 5.13 График плотности гамма-распределения

Рассчитанные при этом по теоретическим формулам моменты таковы:

T=160.94; s.k.o=47.0426; Sk=0.69948; Ex=0.7339. Приведем на рис. 5.14 также результаты оценки критерия согласия полученного Гамма-распределения эмпирическим данным.

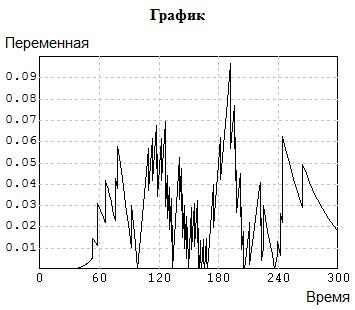
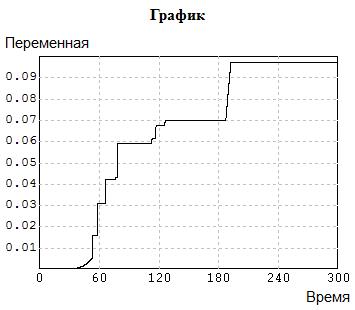
Рис. 5.14. Расчет статистики Колмогорова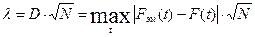

Нами получена оценка D= 0.097008. Тогда 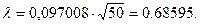И при принятых значениях 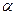=0,05 и 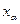=1,358 имеем 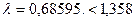. Полученная оценка говорит о том, что нет оснований для отрицания гипотезы о Гамма-распределении.

На рис. 5.15 продемонстрированы наложения аппроксимирующих гамма-распределений с параметрами, полученными методами моментов и максимального правдоподобия.

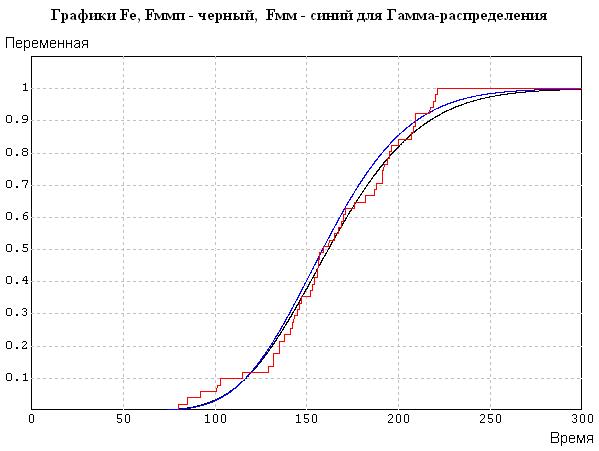
Рис. 5.15 - Наложение полученных результатов на один рисунок

Проделаем такую же работу для распределения Вейбулла, все характеристики представляются в аналитическом виде для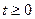

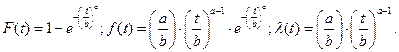
Для определения параметров этого распределения 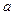и 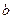мы, как нам известно, приходим к необходимости решения следующего нелинейного алгебраического уравнения

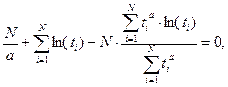
которое надо разрешить относительно оценки параметра 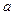, после чего рассчитать и параметр по формуле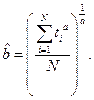

Для решения уравнения будем использовать идею непрерывного градиента и для нахождения 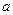решать следующее дифференциальное уравнение:

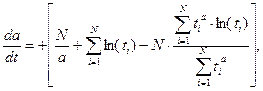
Для этого предварительно нужно подготовить для расчета правую часть уравнения.

Программа 12.

t=time;

init a=1;

N=50;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

L1=ln(t1);L2=ln(t2);L3=ln(t3);L4=ln(t4);L5=ln(t5);L6=ln(t6);L7=ln(t7);L8=ln(t8);

L9=ln(t9);L10=ln(t10);L11=ln(t11);L12=ln(t12);L13=ln(t13);L14=ln(t14);L15=ln(t15);

L16=ln(t16);L17=ln(t17);L18=ln(t18);L19=ln(t19);L20=ln(t20);L21=ln(t21);L22=ln(t22);

L23=ln(t23);L24=ln(t24);L25=ln(t25);L26=ln(t26);L27=ln(t27);L28=ln(t28);L29=ln(t29);

L30=ln(t30);L31=ln(t31);L32=ln(t32);L33=ln(t33);L34=ln(t34);L35=ln(t35);L36=ln(t36);

L37=ln(t37);L38=ln(t38);L39=ln(t39);L40=ln(t40);L41=ln(t41);L42=ln(t42);L43=ln(t43);

L44=ln(t44);L45=ln(t45);L46=ln(t46);L47=ln(t47);L48=ln(t48);L49=ln(t49);L50=ln(t50);

T1=t1^a;T2=t2^a;T3=t3^a;T4=t4^a;T5=t5^a;T6=t6^a;T7=t7^a;T8=t8^a;T9=t9^a;

T10=t10^a;T11=t11^a;T12=t12^a;T13=t13^a;T14=t14^a;T15=t15^a;T16=t16^a;T17=t17^a;

T18=t18^a;T19=t19^a;T20=t20^a;T21=t21^a;T22=t22^a;T23=t23^a;T24=t24^a;T25=t25^a;

T26=t26^a;T27=t27^a;T28=t28^a;T29=t29^a;T30=t30^a;T31=t31^a;T32=t32^a;T33=t33^a;

T34=t34^a;T35=t35^a;T36=t36^a;T37=t37^a;T38=t38^a;T39=t39^a;T40=t40^a;T41=t41^a;

T42=t42^a;T43=t43^a;T44=t44^a;T45=t45^a;T46=t46^a;T47=t47^a;T48=t48^a;T49=t49^a;

T50=t50^a;

SummaLn=250.9313;

SummaTa=T1+T2+T3+T4+T5+T6+T7+T8+T9+T10+T11+T12+T13+T14+T15+T16+T17+T18+T19+T20+

+T21+T22+T23+T24+T25+T26+T27+T28+T29+T30+T31+T32+T33+T34+T35+T36+T37+T38+T39+T40+

+T41+T42+T43+T44+T45+T46+T47+T48+T49+T50;

ProizvLT=T1*L1+T2*L2+T3*L3+T4*L4+T5*L5+T6*L6+T7*L7+T8*L8+T9*L9+T10*L10+T11*L11+

T12*L12+T13*L13+T14*L14+T15*L15+T16*L16+T17*L17+T18*L18+T19*L19+T20*L20+T21*L21+

+T22*L22+T23*L23+T24*L24+T25*L25+T26*L26+T27*L27+T28*L28+T29*L29+T30*L30+T31*L31+

+T32*L32+T33*L33+T34*L34+T35*L35+T36*L36+T37*L37+T38*L38+T39*L39+T40*L40+T41*L41+

+T42*L42+T43*L43+T44*L44+T45*L45+T46*L46+T47*L47+T48*L48+T49*L49+T50*L50;

G=(N/a)+SummaLn-N*ProizvLT/SummaTa;

a'=G;

{a=3.48278}

b=(SummaTa/N)^(1/a); {b=179.173}

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

Fe=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

output Fe,a,b;

Результаты решения a=3.48278, b=179.173.

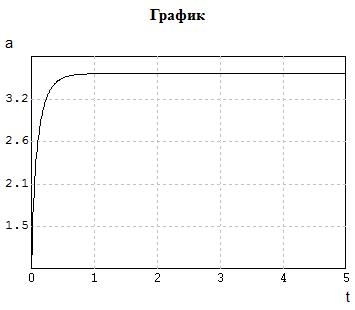
Рис. 5.16 График расчета параметра a

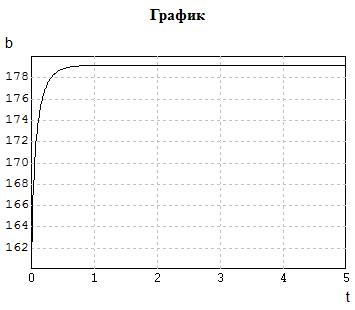
Рис. 5.17 График расчета параметра b

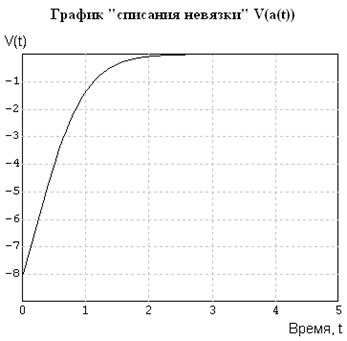
Рис. 5.18 - График «списания невязки»

Наложим график распределения Вейбулла с параметрами, полученными методом максимального правдоподобия, на график эмпирической функции (см. рис. 5.19) и рассчитаем параметры для оценки критерия согласия Колмогорова (см. рис. 5.20).

Программа 13.

t=time;

init a=1,Fw=0,Y=0;

N=50;

t1=140;t2=223;t3=58;t4=113;t5=222;t6=192;t7=168;

t8=225;t9=182;t10=239;t11=149;t12=53;t13=126;t14=66;

t15=242;t16=165;t17=145;t18=159;t19=205;t20=196;t21=130;

t22=122;t23=143;t24=244;t25=78;t26=244;t27=160;t28=198;

t29=175;t30=76;t31=162;t32=147;t33=211;t34=225;t35=203;

t36=153;t37=92;t38=117;t39=133;t40=109;t41=142;t42=128;

t43=132;t44=202;t45=156;t46=126;t47=192;t48=264;t49=197;t50=118;

L1=ln(t1);L2=ln(t2);L3=ln(t3);L4=ln(t4);L5=ln(t5);L6=ln(t6);L7=ln(t7);L8=ln(t8);

L9=ln(t9);L10=ln(t10);L11=ln(t11);L12=ln(t12);L13=ln(t13);L14=ln(t14);L15=ln(t15);

L16=ln(t16);L17=ln(t17);L18=ln(t18);L19=ln(t19);L20=ln(t20);L21=ln(t21);L22=ln(t22);

L23=ln(t23);L24=ln(t24);L25=ln(t25);L26=ln(t26);L27=ln(t27);L28=ln(t28);L29=ln(t29);

L30=ln(t30);L31=ln(t31);L32=ln(t32);L33=ln(t33);L34=ln(t34);L35=ln(t35);L36=ln(t36);

L37=ln(t37);L38=ln(t38);L39=ln(t39);L40=ln(t40);L41=ln(t41);L42=ln(t42);L43=ln(t43);

L44=ln(t44);L45=ln(t45);L46=ln(t46);L47=ln(t47);L48=ln(t48);L49=ln(t49);L50=ln(t50);

T1=t1^a;T2=t2^a;T3=t3^a;T4=t4^a;T5=t5^a;T6=t6^a;T7=t7^a;T8=t8^a;T9=t9^a;

T10=t10^a;T11=t11^a;T12=t12^a;T13=t13^a;T14=t14^a;T15=t15^a;T16=t16^a;T17=t17^a;

T18=t18^a;T19=t19^a;T20=t20^a;T21=t21^a;T22=t22^a;T23=t23^a;T24=t24^a;T25=t25^a;

T26=t26^a;T27=t27^a;T28=t28^a;T29=t29^a;T30=t30^a;T31=t31^a;T32=t32^a;T33=t33^a;

T34=t34^a;T35=t35^a;T36=t36^a;T37=t37^a;T38=t38^a;T39=t39^a;T40=t40^a;T41=t41^a;

T42=t42^a;T43=t43^a;T44=t44^a;T45=t45^a;T46=t46^a;T47=t47^a;T48=t48^a;T49=t49^a;

T50=t50^a;

SummaLn=250.9313;

SummaTa=T1+T2+T3+T4+T5+T6+T7+T8+T9+T10+T11+T12+T13+T14+T15+T16+T17+T18+T19+T20+

+T21+T22+T23+T24+T25+T26+T27+T28+T29+T30+T31+T32+T33+T34+T35+T36+T37+T38+T39+T40+

+T41+T42+T43+T44+T45+T46+T47+T48+T49+T50;

ProizvLT=T1*L1+T2*L2+T3*L3+T4*L4+T5*L5+T6*L6+T7*L7+T8*L8+T9*L9+T10*L10+T11*L11+

T12*L12+T13*L13+T14*L14+T15*L15+T16*L16+T17*L17+T18*L18+T19*L19+T20*L20+T21*L21+

+T22*L22+T23*L23+T24*L24+T25*L25+T26*L26+T27*L27+T28*L28+T29*L29+T30*L30+T31*L31+

+T32*L32+T33*L33+T34*L34+T35*L35+T36*L36+T37*L37+T38*L38+T39*L39+T40*L40+T41*L41+

+T42*L42+T43*L43+T44*L44+T45*L45+T46*L46+T47*L47+T48*L48+T49*L49+T50*L50;

G=(N/a)+SummaLn-N*ProizvLT/SummaTa;

a'=G;

{a=3.48278}

b=(SummaTa/N)^(1/a); {b=179.173}

a1=3.48278;

b1=179.173;

f=(a1/b1)*((t/b1)^(a1-1))*exp(-(t/b1)^a1);

Fw'=f;

x1=step(t1,0,1);x2=step(t2,0,1);x3=step(t3,0,1);x4=step(t4,0,1);x5=step(t5,0,1);

x6=step(t6,0,1);x7=step(t7,0,1);x8=step(t8,0,1);x9=step(t9,0,1);x10=step(t10,0,1);

x11=step(t11,0,1);x12=step(t12,0,1);x13=step(t13,0,1);x14=step(t14,0,1);x15=step(t15,0,1);

x16=step(t16,0,1);x17=step(t17,0,1);x18=step(t18,0,1);x19=step(t19,0,1);x20=step(t20,0,1);

x21=step(t21,0,1);x22=step(t22,0,1);x23=step(t23,0,1);x24=step(t24,0,1);x25=step(t25,0,1);

x26=step(t26,0,1);x27=step(t27,0,1);x28=step(t28,0,1);x29=step(t29,0,1);x30=step(t30,0,1);

x31=step(t31,0,1);x32=step(t32,0,1);x33=step(t33,0,1);x34=step(t34,0,1);x35=step(t35,0,1);

x36=step(t36,0,1);x37=step(t37,0,1);x38=step(t38,0,1);x39=step(t39,0,1);x40=step(t40,0,1);

x41=step(t41,0,1);x42=step(t42,0,1);x43=step(t43,0,1);x44=step(t44,0,1);x45=step(t45,0,1);

x46=step(t46,0,1);x47=step(t47,0,1);x48=step(t48,0,1);x49=step(t49,0,1);x50=step(t50,0,1);

Fe=(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14+x15+x16+x17+x18+x19+x20+

+x21+x22+x23+x24+x25+x26+x27+x28+x29+x30+x31+x32+x33+x34+x35+x36+x37+x38+x39+x40+

+x41+x42+x43+x44+x45+x46+x47+x48+x49+x50)/50;

{Êðèòåðèé ñîãëàñèÿ Êîëìîãîðîâà}

y=abs(Fe-Fw);

Y'=10*(1+sign(y-Y));

output Fe,Fw,a,b,f,y,Y;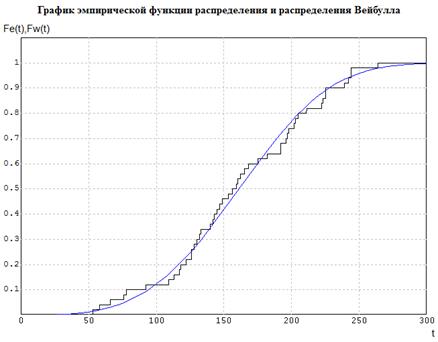

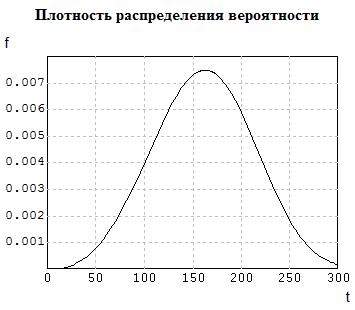
Рис. 5.19

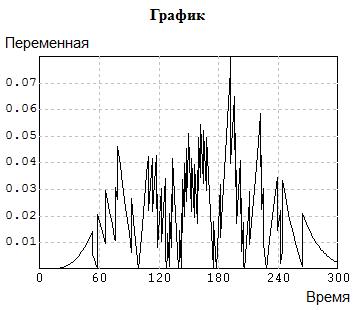
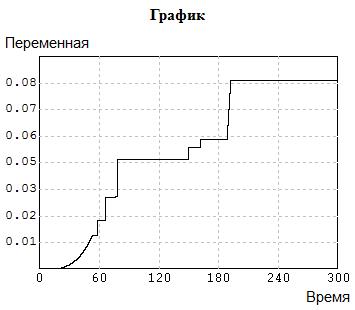
Рис. 5.20

Рассчитаем центральные моменты для полученного аппроксимирующего распределения Вейбулла при a=3.4828; b=179,173.

Результат таков: с.к.о. = 51.2941; Sk= -0.288577; Ex= -0.409101

5.5 Развитие метода максимального правдоподобия

Имея цензурированную выборку, рассчитать параметры предполагаемого теоретического распределения обычным методом максимального правдоподобия не получится. Его нужно усовершенствовать.

Приведем пример программы в МВТУ, рассчитывающей параметры распределения усовершенствованным методом максимального правдоподобия.

Программа.

t=time;

init a=1;

N=100;

t1=37.4016;t2=50.2728;t3=52.5291;t4=52.5291;t5=53.4032;t6=53.4406;t7=58.0694;

t8=67.2218;t9=69.1125;t10=79.7627;

t11=79.9546;t12=80.6018;t13=81.2688;t14=81.9584;

t15=84.0992;t16=89.3357;t17=89.4854;t18=93.7301;t19=98.052;t20=101.848;t21=106.263;

t22=108.239;t23=109.19;t24=109.733;t25=110.322;t26=112.915;t27=115.432;t28=118.202;

t29=121.33;t30=122.268;t31=123.717;t32=126.082;t33=126.805;t34=134.645;t35=135.435;

t36=136.144;t37=140.381;t38=143.135;t39=143.14;t40=143.145;t41=144.899;t42=145.882;

t43=147.046;t44=148.499;t45=149.848;t46=150.263;t47=150.488;t48=150.504;t49=156.174;t50=159.825;

t51=165.835;t52=167.562;t53=167.829;t54=171.408;t55=176.67;t56=180.494;t57=182.478;t58=184.263;

t59=185.41;t60=187.688;t61=191.661;t62=192.387;t63=196.13;t64=198.415;t65=199.738;t66=200.533;

t67=200.827;t68=201.658;t69=203.259;t70=204.411;t71=204.423;t72=206.576;t73=210.069;t74=212.88;

t75=214.061;t76=214.535;t77=216.04;t78=217.424;t79=219.624;t80=220.772;

t81=221.958;t82=223.243;

t83=225.122;t84=225.521;t85=225.787;t86=228.971;t87=229.115;t88=229.767;t89=230.124;t90=233.83;

t91=238.465;t92=238.731;t93=242.733;t94=247.148;t95=251.143;t96=253.053;t97=276.027;t98=279.369;

t99=300.081;t100=303.28;

L1=ln(t1);L2=ln(t2);L3=ln(t3);L4=ln(t4);L5=ln(t5);L6=ln(t6);L7=ln(t7);L8=ln(t8);

L9=ln(t9);L10=ln(t10);L11=ln(t11);L12=ln(t12);L13=ln(t13);L14=ln(t14);L15=ln(t15);

L16=ln(t16);L17=ln(t17);L18=ln(t18);L19=ln(t19);L20=ln(t20);L21=ln(t21);L22=ln(t22);

L23=ln(t23);L24=ln(t24);L25=ln(t25);L26=ln(t26);L27=ln(t27);L28=ln(t28);L29=ln(t29);

L30=ln(t30);L31=ln(t31);L32=ln(t32);L33=ln(t33);L34=ln(t34);L35=ln(t35);L36=ln(t36);

L37=ln(t37);L38=ln(t38);L39=ln(t39);L40=ln(t40);L41=ln(t41);L42=ln(t42);L43=ln(t43);

L44=ln(t44);L45=ln(t45);L46=ln(t46);L47=ln(t47);L48=ln(t48);L49=ln(t49);L50=ln(t50);

L51=ln(t51);L52=ln(t52);L53=ln(t53);L54=ln(t54);L55=ln(t55);L56=ln(t56);L57=ln(t57);

L58=ln(t58);L59=ln(t59);L60=ln(t60);L61=ln(t61);L62=ln(t62);L63=ln(t63);L64=ln(t64);

L65=ln(t65);L66=ln(t66);L67=ln(t67);L68=ln(t68);L69=ln(t69);L70=ln(t70);L71=ln(t71);

L72=ln(t72);L73=ln(t73);L74=ln(t74);L75=ln(t75);L76=ln(t76);L77=ln(t77);L78=ln(t78);

L79=ln(t79);L80=ln(t80);L81=ln(t81);L82=ln(t82);L83=ln(t83);L84=ln(t84);L85=ln(t85);

L86=ln(t86);L87=ln(t87);L88=ln(t88);L89=ln(t89);L90=ln(t90);L91=ln(t91);L92=ln(t92);

L93=ln(t93);L94=ln(t94);L95=ln(t95);L96=ln(t96);L97=ln(t97);L98=ln(t98);L99=ln(t99);

L100=ln(t100);

T1=t1^a;T2=t2^a;T3=t3^a;T4=t4^a;T5=t5^a;T6=t6^a;T7=t7^a;T8=t8^a;T9=t9^a;

T10=t10^a;T11=t11^a;T12=t12^a;T13=t13^a;T14=t14^a;T15=t15^a;T16=t16^a;T17=t17^a;

T18=t18^a;T19=t19^a;T20=t20^a;T21=t21