Алгоритмы расчета параметров распределений методом моментов

2.1. Алгоритмы расчета параметров гамма-распределения методом моментов и его развитие

Классический метод моментов основан, как отмечалось выше, на сопоставлении эмпирических моментов, найденных по статистическим данным эксплуатации, с теоретическими моментами, связанными аналитическими выражениями с параметрами рассматриваемых распределений (см. Приложение 1). При этом используются два первых момента – точечные оценки математического ожидания 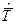и дисперсии 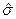, являющиеся при правильной обработке информации состоятельными и несмещенными. 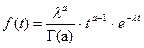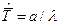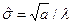Так, например, для гамма - распределения с плотностью вероятности имеют место соотношения (уравнения) и , которые легко разрешаются относительно 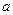и .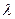

В общем, вычислительных проблем не возникает. Однако имеющаяся важная экспериментальная информация об оценках коэффициентов асимметрии 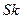и эксцесса 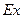совершенно не используется. И это требует в последующих работах, как отмечено во Введении, развития метода моментов.

.2. Алгоритмы расчета параметров распределения Вейбулла

Для распределения Вейбулла соотношения эмпирических моментов с параметрами распределения (см. Приложение 1) имеют вид:

- для математического ожидания (среднего времени наработки до отказа — T ):

;

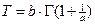- для дисперсии D и среднеквадратического отклонения σ:

; ;

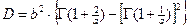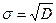- для коэффициента асимметрии Sk («скоса» — skewness):

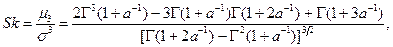
- для коэффициента эксцесса Ex («островершинности» — excess) :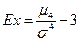

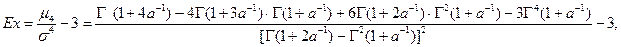
Для нахождения двух неизвестных параметров a и b достаточно использовать два первых соотношения, заменив теоретические значения моментов их выборочным несмещенным оценкам.

Выражая параметр b из соотношения для первого момента

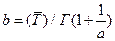
и подставляя его во второе соотношение, мы получаем алгебраическое уравнение для параметра а: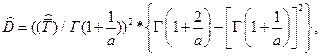

где величины с «тильдой» означают выборочные моменты.

Для нахождения значения параметра a построим (для конкретных данных) график функции

.

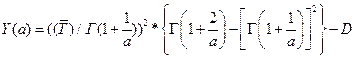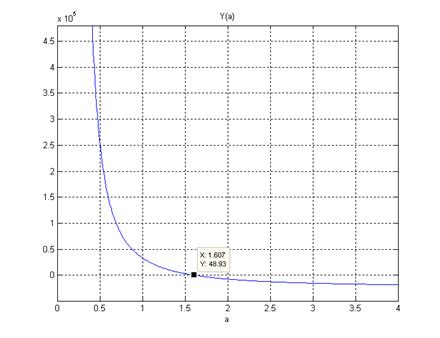
И просто найдём точку пересечения графика с осью абсцисс. Воспользовавшись полученным значением параметра a, вычислим значение параметра b.

Заметим и здесь, что информация об асимметрии и об островершинности опять таки не испльзуется.

АЛГОРИТМЫ РАСЧЕТА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ МЕТОДОМ

МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

3.1. Алгоритмы расчета параметров гамма-распределения

Для гамма-распределение с плотностью

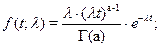
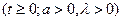
функция правдоподобия имеет вид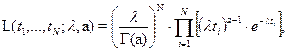

где 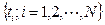— полная выборка наработок до отказа, 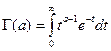— Эйлеров интеграл II рода.

Эквивалентная функция правдоподобия, после логарифмирования функции 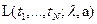, имеет вид

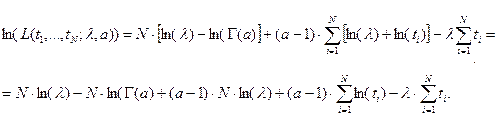
И в окончательном виде

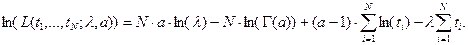
Необходимое условие экстремума:

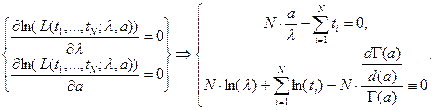
Последний член следует, напомним, из известной формулы для производной функции 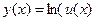, которая такова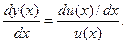

Из первого уравнения следует 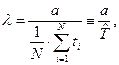где 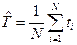- точечная оценка среднего времени наработки до отказа, рассчитанная по полной выборке.

Подставим теперь найденное выражение для 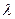во второе уравнение

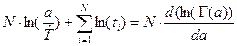
и преобразуем его к виду 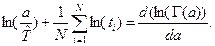(это ).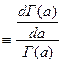

Далее можно записать 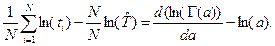Приводя левую часть уравнения к виду 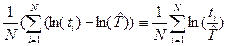, окончательно получим компактное уравнение для получения численной оценки параметра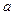

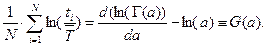
Или в более развернутом виде

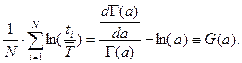
Получив оценку параметра 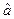, вычисляем и оценку параметра 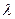по формуле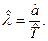

Желательно получить в аналитическом виде и построить график функции 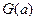. Есть несколько путей получения такой функции. Один из них — в использовании асимптотического разложения Джеймса Стирлинга для гамма-функции.

Асимптотическое разложение для гамма-функции таково

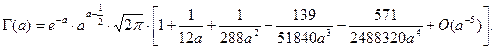
Здесь надо вывести выражение для 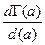и получить 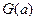в явном виде.

Заметим также, что (см. Справочник Корн и Корн по математик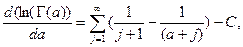е) где 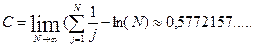е- постоянная Эйлера – Маклорена.

Прямой вычислительный алгоритм нахождения оценок 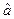и 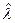для гамма-распределения приведем ниже. А здесь отметим, что умение использовать в расчетах именно гамма-распределение очень важно для практики, т.к. из гамма-распределения вытекают:

- Экспоненциальное распределение при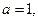

- Распределение Эрланга при целом (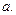

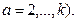
- Хи-квадрат распределение ( 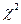- распределение) при 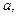кратном 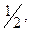и при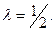

Получим все необходимые соотношения и расчетные формулы

или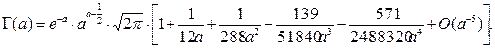

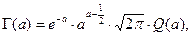
где

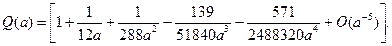
Далее

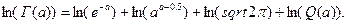
Заметим, что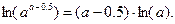

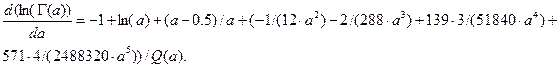
В итоге получим окончательно аналитическое выражение

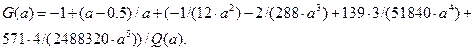
3.2. Алгоритмы расчета параметров распределения Вейбулла для полной выборки

Для этого распределения все характеристики представляются в аналитическом виде

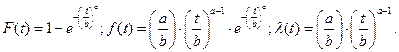
Функции правдоподобия:

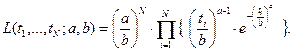
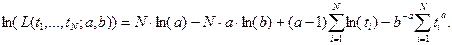
Необходимые условия экстремума:

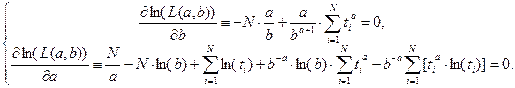
Из первого уравнения находим выражение для

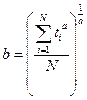
и, подставляя его во второе уравнение, приходим к уравнению:

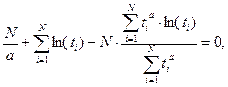
которое надо разрешить относительно параметра 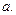При получении последнего уравнения использовано соотношение для коэффициента

.

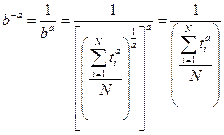С вычислительной точки зрения может быть целесообразнее принять следующую запись этого уравнения

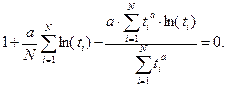
Для решения таких уравнений предлагается использовать идею непрерывного градиента и для нахождения 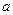решать следующее дифференциальное уравнение:

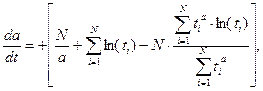
с начальным условием, например 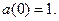Тогда 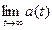даёт искомое значение оценки параметра 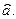После чего остается вычислить 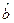по формуле .

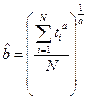3.3. Алгоритмы расчета параметров распределения Вейбулла для цензурированной выборки

Имеем усеченную выборку объемом 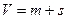, содержащую:

· ряд наработок с отказами ;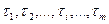

· ряд безотказных наработок .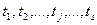

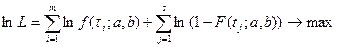
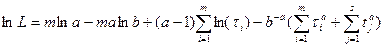
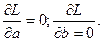
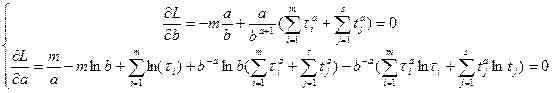
Из первого уравнения: .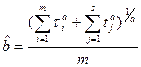

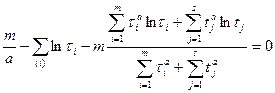
Решаем уравнение и находим параметр a.