Теоретические основы методов моментов и максимального правдоподобия

1.1. Оценка первых четырех выборочных начальных и центральных моментов и построение эмпирического распределения

Расчет точечных оценок всех четырех выборочных начальных и центральных моментов с учетом поправочных коэффициентов для обеспечения несмещенности вычисляемых моментов по следующим формулам.

Оценки начальных эмпирических моментов 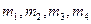рассчитываются по формулам

, ( ),

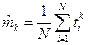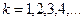через которые в свою очередь могут быть вычислены оценки первых четырех центральных моментов 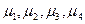по известным связующим соотношениям между ними:

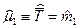- математическое ожидание случайной величины;

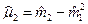- дисперсия;

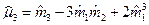- характеристика асимметрии распределения; 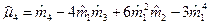- характеристика островершинности распределения.

Оценки центральных моментов могут вычисляться и непосредственно по формулам

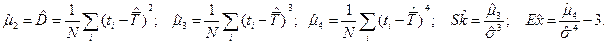
Последние две величины являются нормированными коэффициентами асимметрии и островершинности - 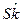- Skewness и 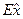- Excess. Для нормального распределения 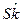= =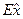0.

Оценки центральных моментов (кроме 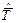) являются смещенными, что при малом числе наблюдений приводит к смещенности параметров предполагаемых («разгадываемых») теоретических распределений случайных величин. Для устранения смещенности оценок центральных моментов от теоретических для генеральной совокупности вводятся поправочные коэффициенты […]:

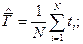
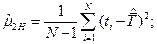
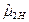( - оценка дисперсии D, 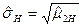- оценка среднеквадратического отклонения);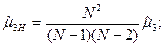

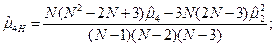
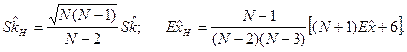
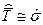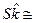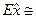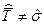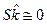На основе полученных численных значений оценок центральных моментов могут выдвигаться гипотезы о предполагаемых теоретических законах распределения. Так, если , 2, а 6, то гипотеза об экспоненциальном (показательном) законе может быть принята к рассмотрению. Если , а и 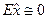, то следует принять к рассмотрению гипотезу о нормальном (гауссовом) законе распределения.

При обработке эмпирических данных может быть проще определить сначала оценки начальных моментов. Затем найти смещенные оценки центральных моментов и, наконец, вычислить несмещенные оценки.

Если последовательность результатов независимых наблюдений 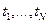над случайной величиной 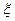с функцией распределения 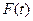расположить в порядке возрастания 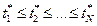, то получается так называемыйвариационный ряд.

Эмпирической функцией распределения 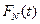называется функция, определенная равенствами:

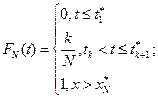
Таким образом, эмпирическая функция при каждом значении x равна числу значений случайной величины, меньших x, деленному на общее число наблюдений.

1.2. Метод моментов

Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов (см. Приложение 1) соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка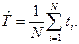

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка. Так, для гамма-распределения параметры очень просто рассчитываются методом моментов исходя из приравнивания несмещенных оценок дисперсий и математических ожиданий эмпирического закона распределения с теоретическими для данного распределения 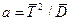; 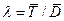, где в правые части подставляются соответственно выборочные оценки математического ожидания и дисперсии.

Для более сложных распределений, например для распределения Вейбулла-Гнеденко, задача сводится к необходимости решения сложнейших алгебраических уравнений, рассматриваемых ниже.

1.3 Метод максимального правдоподобия (ММП)

Метод максимального правдоподобия (метод МП) предложен Рональд Айлмер Фишером в 1912. Идея ММП такова.

В ходе сбора и обработки данных о наработках и отказах объекта (изделия, устройства) получена информация, которую будем рассматривать как полную выборку из генеральной совокупности исследуемых объектов 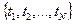. Эта выборка 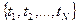- совокупность возможных значений независимых, одинаково распределенных случайных величин.

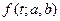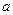Принимается гипотеза о виде функции распределения или плотности распределения , где и 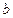- параметры распределения, подлежащие определению.

Исследуется вероятность получения выборки 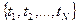, рассматриваемой как совокупность возможных значений независимых, одинаково распределенных случайных величин. Эта вероятность равна:

,

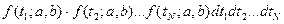где 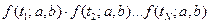– совместная плотность распределения векторной случайной величины с компонентами 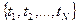. Это вероятность того, что будут получены отказы в моменты .

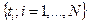Вводится функция правдоподобия

,

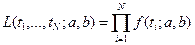которая должна быть максимизирована по параметрам 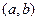. Это оценка вероятности появления сложного события - совместного появления значений элементов выборки .

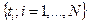Пусть 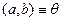– вектор параметров. Тогда оценкой максимального правдоподобия неизвестного вектора 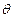распределения непрерывной случайной величины называют такое его значение 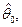для которого функция правдоподобия 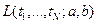принимает наибольшее значение при полученных выборочных данных 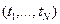. Это можно в общем виде записать

.

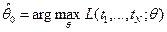Необходимое и достаточное условие максимума 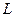в точке 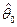имеет вид:

; .

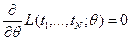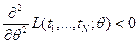Выражение в левой части неравенства представляет собой матрицу Гессе, которая должна быть симметричной и отрицательно определенной. При наличии нескольких максимумов необходимо выбрать наибольший.

Удобно использовать функцию 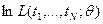, имеющую максимум в той же точке, что и 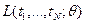. Если 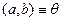, т.е. имеем два параметра, то необходимые условия оптимальности представляют собой два алгебраические уравнения

,

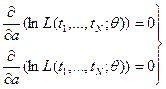которые и являются уравнениями правдоподобия. Решение системы уравнений дает оптимальные значения параметров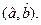

При выполнении достаточно общих условий эти оценки являются состоятельными и асимптотически эффективными. В общем случае оценки 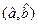являются смещенными (см. на с. 544 в кн. Крамер Г. «Математические методы статистики». – М.: Мир, 1975. – 648 с.). В литературе отмечается, что метод максимального правдоподобия является достаточно универсальным и плодотворным методом оценивания. Более того, он полезен и при малых выборках, в том числе усеченных (или цензурированных), алгоритмы обработки которых мы рассмотрим ниже.

Здесь же рассмотрим уравнения правдоподобия для наиболее употребительных стандартных распределений.

Для экспоненциального распределения с плотностью вероятности 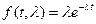функция правдоподобия имеет вид 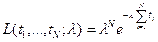или .

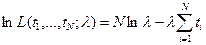Необходимое условие экстремума при этом имеет вид 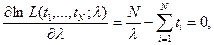из которого находим решение 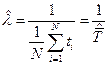. Кроме того, очевидно, что 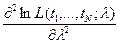при 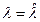равна 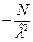, то есть отрицательна. Значит, оценка 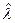есть оценка максимального правдоподобия.

Для нормального распределения с плотностью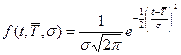

функция правдоподобия 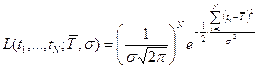или

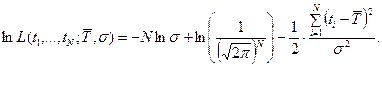
Необходимые условия экстремум

.

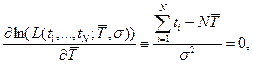
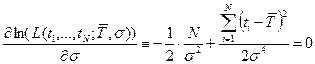Решая эту систему уравнений, получим искомые оценк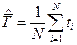и

и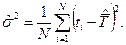

Заметим, что оценка дисперсии смещена. И следует ввести поправку Бесселя, т.е. умножить на коэффициент N/(N-1).Матрица Гессе – диагональная с отрицательными элементами на главной диагонали .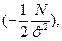

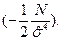Для других более «сложных» распределений решение задачи существенно усложняется в связи с необходимостью решение достаточно сложных нелинейных алгебраических уравнений. И мы их рассмотрим более подробно ниже.

.4 О методе «вероятностной бумаги»

График функции распределения можно представить в виде совокупности точек (t, p) на плоскости, где 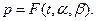Основная идея графического метода состоит в том, что подбирается такая непрерывная замена координат 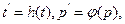что при этом график функции распределения 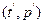, где 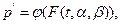становится прямой линией 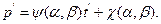Если такую замену переменных удалось отыскать, то на плоскости 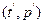любая функция распределения этого семейства будет представима в виде прямой 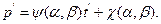Или, что то же самое, в виде прямой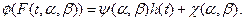

Используем этот факт для оценки параметров 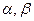. Предположим, что в результате испытаний получены N значений некоторой случайной величины (например, времени безотказной работы элемента или интервалов между отказами в аппаратуре). По этим значениям мы построили эмпирическую функцию распределения. Полученная эмпирическая функция при больших N лежит вблизи от теоретической функции распределения 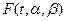. Тогда после замены переменных график 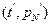будет лежать в непосредственной близости от графика 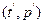, являющегося прямой. Оценив тангенс наклона k и свободный член b и приравняв их теоретическим значениям, получаем уравнения 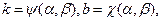из которых находим оценки неизвестных значений параметров .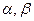