Действительные и виртуальные перемещения
Пусть в момент времени 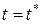 система находится в положении
система находится в положении 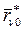 , а скорости ее точек имеют конкретные возможные значения
, а скорости ее точек имеют конкретные возможные значения 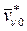 . Если известны силы, действующие на систему, то, проинтегрировав дифференциальные уравнения динамики, можно получить значения радиус-векторов
. Если известны силы, действующие на систему, то, проинтегрировав дифференциальные уравнения динамики, можно получить значения радиус-векторов 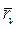 для моментов времени t, следующих за t*. Обозначим
для моментов времени t, следующих за t*. Обозначим 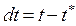 . Тогда приращение радиус-векторов точек системы можно представить в виде
. Тогда приращение радиус-векторов точек системы можно представить в виде
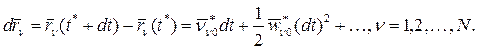
Величины 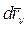 есть действительные перемещения точек системы за время dt. Действительные перемещения всегда являются одними из возможных. Если предположить, что действительные перемещения системы линейны по dt, т.е.
есть действительные перемещения точек системы за время dt. Действительные перемещения всегда являются одними из возможных. Если предположить, что действительные перемещения системы линейны по dt, т.е.  , то эти перемещения будут удовлетворять уравнениям, вытекающим из (2) и (3):
, то эти перемещения будут удовлетворять уравнениям, вытекающим из (2) и (3):
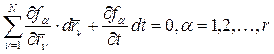 , (7)
, (7)
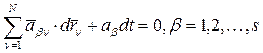 . (8)
. (8)
Виртуальным перемещением механической системы называется совокупность величин 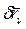 , удовлетворяющая линейным однородным уравнениям
, удовлетворяющая линейным однородным уравнениям
 , (9)
, (9)
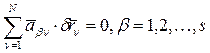 . (10)
. (10)
где 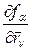 ,
, 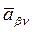 вычисляются при
вычисляются при 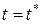 ,
, 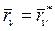 . Очевидно, что для склерономной механической системы действительное перемещение будет одним из виртуальных, т.к. связи в склерономной системе явно от времени не зависят.
. Очевидно, что для склерономной механической системы действительное перемещение будет одним из виртуальных, т.к. связи в склерономной системе явно от времени не зависят.
Числом степеней свободы механической системы называется число ее независимых виртуальных перемещений
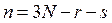 , (11)
, (11)
где r – число голономных и s – число неголономных связей, действующих в механической системе, N – число точек системы.
Задача
Задан жесткий треугольник с вершинами P1, P2 и P3, движущийся в трехмерном пространстве (рис. 8). Найти число степеней свободы треугольника.
Решение
Известно, что точка в трехмерном пространстве имеет три независимых виртуальных перемещения и, следовательно, три степени свободы. Предположим, что вершины треугольника между собой не связаны. Тогда механическая система из трех точек имела бы 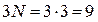 степеней свободы. Однако, по условию задачи треугольник жесткий и расстояния между его вершинами постоянны. Это условие записывается тремя аналитическими уравнениями связей
степеней свободы. Однако, по условию задачи треугольник жесткий и расстояния между его вершинами постоянны. Это условие записывается тремя аналитическими уравнениями связей
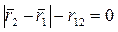 ,
, 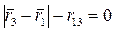 ,
, 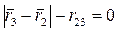 ,
,
где 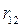 ,
, 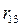 и
и 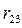 - длины сторон треугольника. Все три уравнения описывают геометрические стационарные связи; следовательно, жесткий треугольник – голономная склерономная система. Имеем: r = 3, s = 0 и число степеней свободы, согласно (11),
- длины сторон треугольника. Все три уравнения описывают геометрические стационарные связи; следовательно, жесткий треугольник – голономная склерономная система. Имеем: r = 3, s = 0 и число степеней свободы, согласно (11), 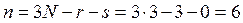 . Таким образом, жесткий треугольник (простейшее пространственное твердое тело) имеет шесть степеней свободы.
. Таким образом, жесткий треугольник (простейшее пространственное твердое тело) имеет шесть степеней свободы.
Обобщенные координаты
Наименьшее число параметров, необходимое для задания возможного положения механической системы, называется числом ее обобщенных координат. Так как уравнения связей (2) независимы, то число обобщенных координат
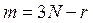 . (12)
. (12)
Из (11) и (12) следует, что число степеней свободы системы в общем случае не равно числу ее обобщенных координат. Равенство 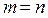 имеет место только в случае
имеет место только в случае 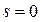 , т.е. голономной механической системы. Выбор обобщенных координат может быть произвольным; например, за обобщенные координаты можно принять m из 3N декартовых координат
, т.е. голономной механической системы. Выбор обобщенных координат может быть произвольным; например, за обобщенные координаты можно принять m из 3N декартовых координат 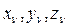 точек механической системы. Однако, как правило, такой выбор практически малопригоден. Можно ввести любые другие m независимых величин
точек механической системы. Однако, как правило, такой выбор практически малопригоден. Можно ввести любые другие m независимых величин 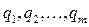 , в своей совокупности определяющих конфигурацию системы. Эти координаты могут иметь геометрический смысл расстояний, углов, площадей и т.п. Требуется только, чтобы они были независимы, а радиус-векторы точек можно было представить в виде
, в своей совокупности определяющих конфигурацию системы. Эти координаты могут иметь геометрический смысл расстояний, углов, площадей и т.п. Требуется только, чтобы они были независимы, а радиус-векторы точек можно было представить в виде
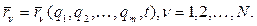
При решении конкретных задач механики часто нет необходимости составлять уравнения связей (2). Из физической сущности задачи обычно ясно, как надо выбирать обобщенные координаты в таком количестве, которое необходимо и достаточно для задания возможных положений механической системы.
|
|
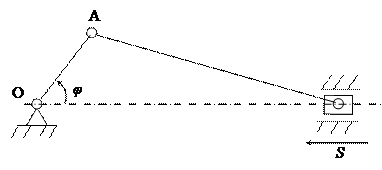
Для кривошипно-ползунного механизма, изображенного на рис. 28, определить закон движения S(t) ползуна B и вычислить его скорость.
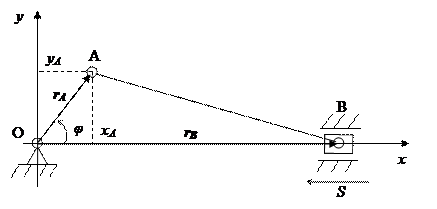 Решение
Решение
|
Введем неподвижную декартовую систему координат Oxy, поместив ее начало на оси вращения кривошипа OA (рис. 29). Рассмотрим движение шарниров А и B. Шарнир A движется по окружности радиуса R относительно оси O. Следовательно, его возможные положения определяются равенством
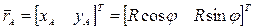 . Шарнир B движется поступательно вдоль оси x. Его положение определяется радиус-вектором
. Шарнир B движется поступательно вдоль оси x. Его положение определяется радиус-вектором 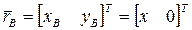 . Шарниры A и B связаны между собой шатуном, поэтому расстояние между ними всегда равно L. Это условие определяется уравнением связи
. Шарниры A и B связаны между собой шатуном, поэтому расстояние между ними всегда равно L. Это условие определяется уравнением связи 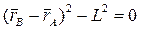 . Подставляя в последнее уравнение соотношения для
. Подставляя в последнее уравнение соотношения для 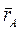 и
и 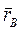 , получим
, получим
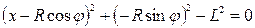 ,
,
откуда следует квадратное уравнение относительно x:
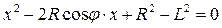 .
.
Полученное уравнение имеет два решения: 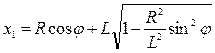 ,
, 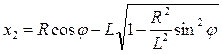 . Очевидно, что решение x1 соответствует механизму, изображенному на рис. 29. Решение x2 соответствует случаю, когда ползун B движется в отрицательной области значений x. Следовательно,
. Очевидно, что решение x1 соответствует механизму, изображенному на рис. 29. Решение x2 соответствует случаю, когда ползун B движется в отрицательной области значений x. Следовательно, 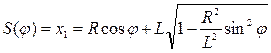 и
и 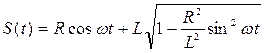 . Скорость ползуна B найдем, продифференцировав по времени t закон движения S(t):
. Скорость ползуна B найдем, продифференцировав по времени t закон движения S(t):
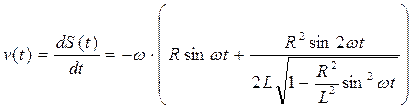 .
.
Рассмотренный метод, основанный на аналитическом описании наложенных на точки механической системы связей, часто позволяет получить решение сложной задачи без необходимости выполнения геометрических построений. При этом точность вычисления искомых величин будет зависеть только от точности представления исходных данных, так как эти величины отыскиваются в виде аналитических зависимостей. Решим задачу, приведенную в п. 2.7, используя аналитическое описание связей.
 | |||
|
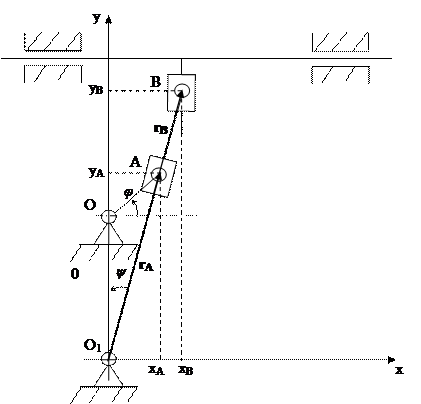
Обозначим R – радиус кривошипа OA, a – расстояние O1O, L – длина кулисы O1B. Введем декартовую систему координат O1xy, связанную с неподвижной стойкой механизма (рис. 30). Тогда радиус вектор 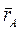 , задающий положение шарнира A будет определяться равенством:
, задающий положение шарнира A будет определяться равенством:
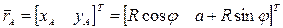 .
.
Следовательно, 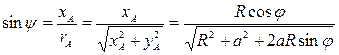 и
и
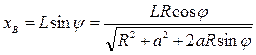 .
.
Согласно условию задачи 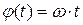 , ω = const, поэтому закон движения суппорта станка
, ω = const, поэтому закон движения суппорта станка 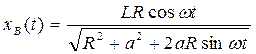 .
.
Скорость суппорта найдем, продифференцировав по времени t закон движения xB(t):
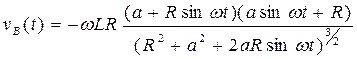 .
.
Повторно продифференцировав полученное равенство, найдем ускорение суппорта:
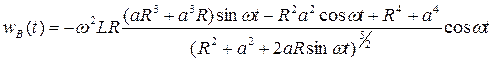 .
.
Теперь, подставив в полученные выражения 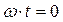 , что соответствует положению механизма в задаче п. 2.7, и исходные данные, получим:
, что соответствует положению механизма в задаче п. 2.7, и исходные данные, получим:
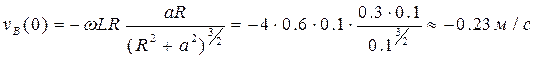 ,
,
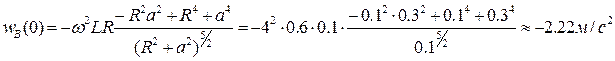 .
.
Значения скорости и ускорения суппорта показывают, что в рассматриваемый момент времени суппорт движется с ускорением в обратном по отношению к оси x направлении. Эти значения соответствуют результату, полученному графическим методом в п. 2.7. Разница в сотых долях объясняется погрешностями, неизбежными при выполнении графических построений. Таким образом, применение метода, основанного на аналитическом описании связей, позволило не только существенно сократить решение, но и получить более точные результаты. Кроме того, для вычисления кинематических параметров суппорта в любой другой момент времени достаточно подставить в формулы для vB(t) и wB(t) соответствующее значение t.
Вопросы для проверки усвоения материала
1) Дайте определение понятию «механическая система».
2) Что в механической системе называется связями?
3) Какие связи называются геометрическими? Приведите примеры механических систем с геометрическими связями.
4) Какие связи называются неголономными? Приведите пример механической системы с неголономной связью.
5) Как в соответствии с классификацией можно назвать связи, наложенные на точки абсолютно твердого тела?
6) Что называют возможными положениями, скоростями и ускорениями механической системы?
7) Что называют возможными перемещениями механической системы?
8) В чем различие между возможным и действительным перемещением механической системы?
9) Что называют виртуальными перемещениями механической системы?
10) В чем различие между числом степеней свободы и числом обобщенных координат механической системы? В каком случае эти числа равны?
СПИСОК ЛИТЕРАТУРЫ
1. Кильчевский Н.А. Курс теоретической механики, т. 1 (кинематика, статика, динамика точки). – М.: Наука, 1977. – 480 с.
2. Маркеев А.П. Теоретическая механика. – М.: Наука, 1990. – 416 с.
3. Мещерский И.В. Сборник задач по теоретической механике: Учебное пособие. – 36-е изд., исправл. / Под ред. Н.В. Бутенина, А.И. Лурье, Д.Р. Меркина. – М.: Наука, 1986. – 448 с.
4. Ольховский И.И. Курс теоретической механики для физиков. – М.: Наука, 1970. – 447 с.
[1] Запись следует читать: «косинус угла между векторами и ».
2 Вектор - это тот же вектор , только заданный в системе координат Oxyz.
3 Матрицей, обратной A, называют матрицу A-1, такую, что A-1A=E, где E – единичная матрица. Матрица AT - транспонированная, в которой строки и столбцы меняются местами.
4 В целях сокращения записей формул в технической литературе используются обозначения:
, .
5 Кососимметрической называют такую матрицу B, для которой справедливо равенство: BT = -B.
6 В данном случае осестремительное ускорение равно нормальному, а вращательное ускорение– тангенциальному.
7 Обозначение читается так: «скорость точки P относительно точки O».
8 Входными в механике называются звенья механизма, через которые к нему поступает механическая энергия от двигателей. Законы движения входных звеньев, как правило, известны.
9 Выходными звеньями называются звенья механизма, совершающие требуемые технологические движения. Вообще, любой механизм можно рассматривать как преобразователь механической энергии двигателей в механическую энергию требуемых технологических движений выходных звеньев.
10 Уравнения (3) – общая форма записи линейных относительно скоростей неголономных связей. Например, неголономная связь из предыдущей задачи в общей форме будет иметь вид: , где , .
