Основы кинематики механической системы
Классификация связей
Дадим определение понятию механическая система. Механической системой в теоретической механике называется совокупность некоторого конечного числа материальных точек. Такими абстрактными системами математически моделируются реальные физические системы, труднодоступные для исследования путем натурного эксперимента (принципиально новые проектируемые изделия и их элементы, природные системы, изменения в которых наблюдаются в течение длительных или, наоборот, очень коротких периодов времени и т.п.). В каждой конкретной задаче существуют ограничения, накладываемые на положения и скорости точек механической системы, которые выполняются при любых действующих на систему силах. Эти ограничения называются связями. Если подобных ограничений нет, то механическая система называется свободной, при наличии одной или нескольких связей система называется несвободной.
Рассмотрим движение системы материальных точек 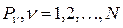 , относительно некоторой прямоугольной декартовой системы координат, полагаемой неподвижной. Состояние механической системы задается радиус-векторами
, относительно некоторой прямоугольной декартовой системы координат, полагаемой неподвижной. Состояние механической системы задается радиус-векторами 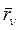 и скоростями
и скоростями 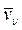 ее точек. В общем случае связь задается функцией
ее точек. В общем случае связь задается функцией
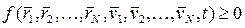 , (1)
, (1)
которая полагается дважды непрерывно дифференцируемой. В дальнейшем, будем использовать сокращенную запись функции (1) - 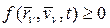 . Если в (1) реализуется знак равенства, то связь называется удерживающей или двухсторонней. Если реализуется знак
. Если в (1) реализуется знак равенства, то связь называется удерживающей или двухсторонней. Если реализуется знак 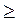 , то связь называется неудерживающей или односторонней. Системы с неудерживающими связями в дальнейшем не рассматриваются. Если уравнение связи можно записать в виде
, то связь называется неудерживающей или односторонней. Системы с неудерживающими связями в дальнейшем не рассматриваются. Если уравнение связи можно записать в виде 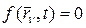 , то связь называется геометрической или голономной. Если в уравнение связи входят проекции скоростей
, то связь называется геометрической или голономной. Если в уравнение связи входят проекции скоростей 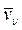 , то связь называется дифференциальной или кинематической. Дифференциальную связь
, то связь называется дифференциальной или кинематической. Дифференциальную связь 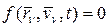 называют интегрируемой, если ее можно представить в виде геометрической связи. Неинтегрируемая дифференциальная связь называется неголономной. Соответственно, механическая система, в которой есть хотя бы одна такая связь, называется неголономной. Связь называется стационарной или склерономной, если она не зависит явно от времени t. Если все связи в механической системе стационарные, то система называется склерономной. В противном случае система будет называться реономной.
называют интегрируемой, если ее можно представить в виде геометрической связи. Неинтегрируемая дифференциальная связь называется неголономной. Соответственно, механическая система, в которой есть хотя бы одна такая связь, называется неголономной. Связь называется стационарной или склерономной, если она не зависит явно от времени t. Если все связи в механической системе стационарные, то система называется склерономной. В противном случае система будет называться реономной.
Задача
Конек движется по льду в горизонтальной плоскости Oxy (рис. 27). Точка C конька во все время движения имеет скорость, направленную вдоль его полоза. Показать, что данная механическая система неголономная.
 |
Решение
Запишем уравнения связей, наложенных на точку C конька. Так как конек все время находится в плоскости Oxy, то первая связь будет задаваться уравнением 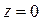 , где z – координата точки C по вертикальной оси. По условию задачи, скорость точки C
, где z – координата точки C по вертикальной оси. По условию задачи, скорость точки C 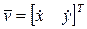 направлена все время вдоль конька. Это ограничение опишется уравнением
направлена все время вдоль конька. Это ограничение опишется уравнением 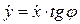 , где φ – угол поворота конька, отсчитываемый от направления оси Ox. Других связей в данной механической системе нет. Очевидно, что связь
, где φ – угол поворота конька, отсчитываемый от направления оси Ox. Других связей в данной механической системе нет. Очевидно, что связь 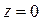 геометрическая, т.к. в ее уравнение входит координата z точки C, но не входят проекции скорости. Связь
геометрическая, т.к. в ее уравнение входит координата z точки C, но не входят проекции скорости. Связь 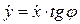 является дифференциальной, т.к. в ее уравнение входят проекции скорости точки C.
является дифференциальной, т.к. в ее уравнение входят проекции скорости точки C.
Предположим, что дифференциальная связь 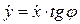 интегрируемая. Тогда ее можно записать как функцию координат x, y, φ и времени t:
интегрируемая. Тогда ее можно записать как функцию координат x, y, φ и времени t: 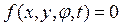 . Пусть x, y и φ отвечают действительному движению конька. Вычислим полную производную функции f по времени:
. Пусть x, y и φ отвечают действительному движению конька. Вычислим полную производную функции f по времени:
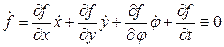 .
.
С учетом уравнения связи 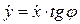 выражение для
выражение для 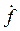 примет вид
примет вид
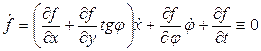 ,
,
откуда, ввиду независимости величин 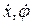 , получим равенства:
, получим равенства:
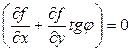 ,
, 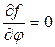 ,
, 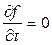 .
.
Ввиду произвольности угла φ из этих равенств следует, что частные производные функции f по всем ее аргументам равны нулю, т.е. f не зависит от x, y, φ и t. Следовательно, предположение об интегрируемости связи 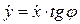 неверно и данная механическая система – неголономная.
неверно и данная механическая система – неголономная.
