Частные случаи движения твердого тела
Твердые тела, входящие в состав механизмов и машин, не могут двигаться произвольно. Их движения ограничиваются за счет контакта в подвижных соединениях механизма и, как правило, представляют собой следующие частные случаи: вращение вокруг неподвижной оси и плоское движение.
Вращение вокруг неподвижной оси
Формулы для скорости и ускорения точки P твердого тела, вращающегося вокруг неподвижной оси OZ, получаются из общих соотношений (3) и (5) путем применения к этим соотношениям частных условий:
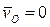 ,
, 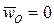 ,
, 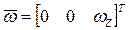 .
.
В результате из (3) следует
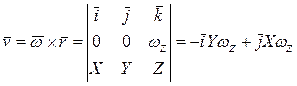 ,
, 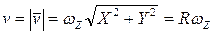 , (6)
, (6)
а из (5)
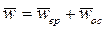 ,
,
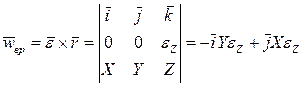 ,
, 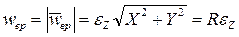 ;
;
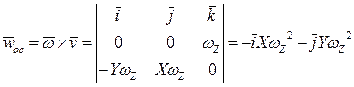 ,
, 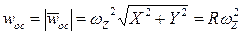 . (7)
. (7)
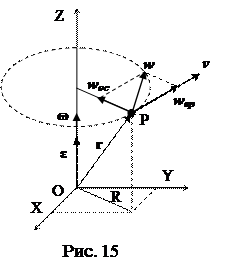
Таким образом, любая точка твердого тела, не лежащая на оси его вращения, движется по окружности радиуса R в плоскости, перпендикулярной оси вращения (рис.15). Формулы (6), (7) соответствуют случаю движения точки по окружности6.
Плоское движение
Движение твердого тела называется плоским, если все точки тела движутся в плоскостях, параллельных неподвижной плоскости.
 | |||||
 | |||||
| |||||
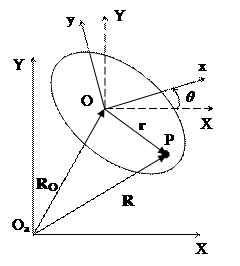
Плоское движение твердого тела эквивалентно движению соответствующей плоской фигуры в собственной плоскости (рис. 16). Фигура имеет свободу по трем независимым перемещениям: вдоль оси OaX, вдоль оси OaY и вращение в плоскости OaXY. Соответственно, любое положение фигуры может быть задано тремя координатами: XO, YO, θ.
Формулы для скорости и ускорения точки P твердого тела, совершающего плоское движение, получаются из общих соотношений (3) и (5) путем применения к этим соотношениям частных условий:
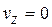 ,
, 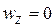 ,
, 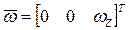 .
.
В результате из (3) следует7
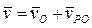 , (8)
, (8)
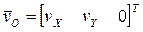 ,
, 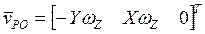 ,
, 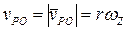 ,
,
а из (5)
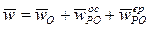 , (9)
, (9)
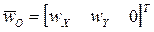 ,
, 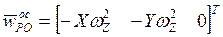 ,
, 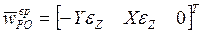 ,
,
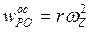 ,
, 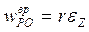 .
.
Таким образом, в случае плоского движения, векторы скорости и ускорения точки твердого тела всегда лежат в плоскости движения, а векторы угловой скорости и углового ускорения всегда перпендикулярны этой плоскости. Этот факт позволяет при решении практических задач оперировать линейными скоростями и ускорениями как векторами в плоскости, а угловыми скоростями и ускорениями – как скалярными величинами.
Задача
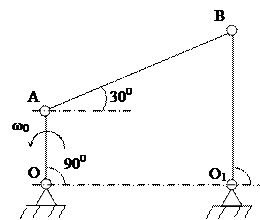
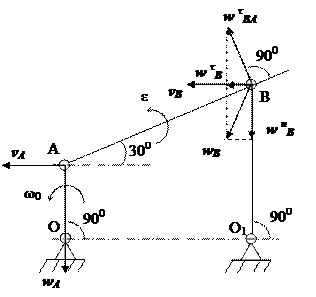 Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
 | |||||
| |||||
| |||||
Решение
Стержень AB изображенного на рисунке четырехзвенного механизма совершает плоское движение, а стержни OA и O1B вращаются вокруг неподвижных центров O и O1. Найдем скорость шарнира A:
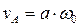 .
.
Вектор 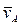 перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
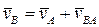 ,
,
причем направление 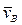 , согласно положению механизма, будет то же, что и у
, согласно положению механизма, будет то же, что и у 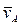 . Из этого следует, что
. Из этого следует, что 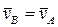 ,
, 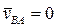 ,
, 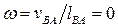 , т.е. стержень AB совершает мгновенно-поступательное движение.
, т.е. стержень AB совершает мгновенно-поступательное движение.
Найдем ускорение шарнира A. Так как этот шарнир движется вокруг неподвижной точки O, то для его ускорения справедливо равенство (7):
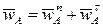 ,
,
где 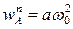 - нормальное ускорение, направленное от точки A к центру вращения O;
- нормальное ускорение, направленное от точки A к центру вращения O; 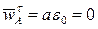 , т.к.
, т.к. 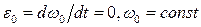 . В данном случае
. В данном случае 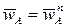 . Для ускорения шарнира B справедливо равенство (9):
. Для ускорения шарнира B справедливо равенство (9):
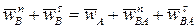 , (10)
, (10)
где 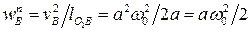 - нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1;
- нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1; 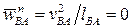 - нормальное ускорение шарнира B относительно точки A.
- нормальное ускорение шарнира B относительно точки A.
Неизвестные по величине векторы 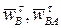 определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение
определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение 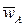 (рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения
(рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения 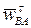 . Составляющую результирующего ускорения
. Составляющую результирующего ускорения 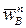 отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление
отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление 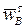 . На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение
. На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение 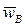 шарнира B, а отрезок ab – ускорение
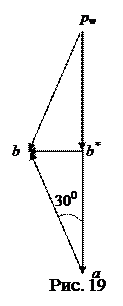
шарнира B, а отрезок ab – ускорение 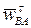 . План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
. План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
 | |||
 | |||
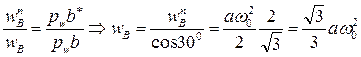 - ускорение шарнира B;
- ускорение шарнира B;
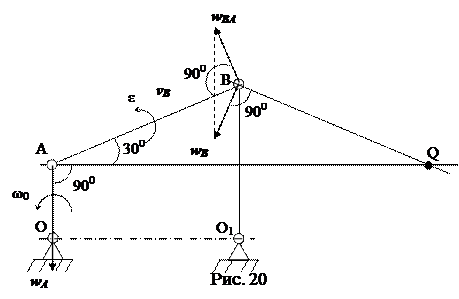
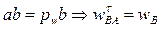 ,
, 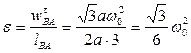 - угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
- угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
В задачах на случай плоского движения твердого тела иногда удается получить более короткое решение за счет использования понятий мгновенный центр скоростей и мгновенный центр ускорений. Мгновенным центром скоростей (МЦС) называют такую точку плоской фигуры, скорость которой в данный момент времени движения равна нулю. Скорости остальных точек фигуры при этом такие, какие они были бы при вращательном движении фигуры вокруг МЦС. Мгновенный центр ускорений (МЦУ), соответственно, это такая точка плоской фигуры, ускорение которой в данный момент времени движения равно нулю. Ускорения остальных точек фигуры такие, какие они были бы при ее вращательном движении относительно МЦУ.
Решим предыдущую задачу, используя понятия МЦС и МЦУ. Из рис. 17 видно, что стержень OA параллелен стержню O1B. Следовательно, абсолютные скорости точек A и B стержня AB параллельны. Учитывая, что в силу неизменности расстояния между точками A и B проекции скоростей 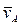 и
и 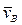 на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что
на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что 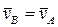 . Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и
. Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и 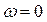 .
.
Определим направление ускорения 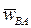 точки B в ее движении относительно точки A. Так как угловая скорость стержня AB
точки B в ее движении относительно точки A. Так как угловая скорость стержня AB 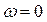 , то
, то 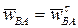 и, следовательно, угол между
и, следовательно, угол между 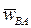 и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением
и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением 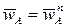 и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при
и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при 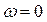 :
:
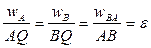 . (11)
. (11)
Вычислим ускорение точки A: 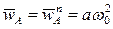 . В силу соотношения
. В силу соотношения 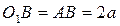 будем иметь
будем иметь 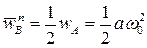 . Так как
. Так как 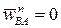 , а
, а 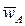 направлено в ту же сторону, что и
направлено в ту же сторону, что и 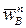 , на основании равенства (10) заключаем:
, на основании равенства (10) заключаем: 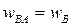 (рис. 19). Следовательно, из (11) получим
(рис. 19). Следовательно, из (11) получим 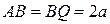 , и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда
, и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда 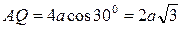 ,
, 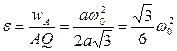 и
и 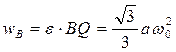 . Угол между
. Угол между 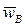 и направлением BQ, согласно определению понятия МЦУ, составит 900.
и направлением BQ, согласно определению понятия МЦУ, составит 900.
Сложное движение точки
Движение точки называется сложным, если оно происходит относительно двух систем координат, одна из которых – подвижная, а другая – неподвижная. Движение точки относительно подвижной системы координат называется относительным, а движение подвижной системы координат относительно неподвижной – переносным. Часто подвижную систему координат связывают с некоторым твердым телом, совершающим движение относительно неподвижной системы координат. При этом полагается, что относительное и переносное движения известны. Задача состоит в том, чтобы определить сложное движение точки в неподвижной (абсолютной) системе координат.
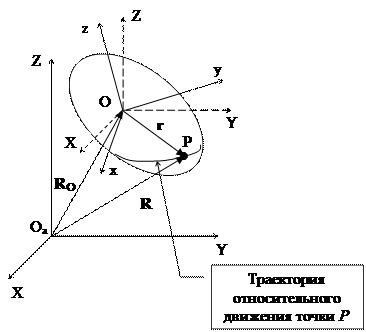 Пусть точка P перемещается по поверхности твердого тела, движущегося произвольным образом относительно абсолютной системы координат OaXYZ (рис. 21).
Пусть точка P перемещается по поверхности твердого тела, движущегося произвольным образом относительно абсолютной системы координат OaXYZ (рис. 21).
|
Система координат OXYZ движется поступательно вместе с центром O твердого тела: 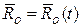 , а система координат Oxyz жестко связана с твердым телом и вращается вокруг центра O:
, а система координат Oxyz жестко связана с твердым телом и вращается вокруг центра O: 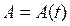 - матрица поворота Oxyz вокруг OXYZ. Радиус-вектор точки P в системе координат Oxyz обозначим
- матрица поворота Oxyz вокруг OXYZ. Радиус-вектор точки P в системе координат Oxyz обозначим 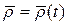 и будем полагать известным. Вычислим абсолютную скорость точки P, воспользовавшись соотношением (2):
и будем полагать известным. Вычислим абсолютную скорость точки P, воспользовавшись соотношением (2):
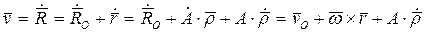 . (12)
. (12)
Обозначив в (12) 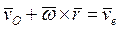 и
и 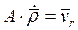 получим:
получим:
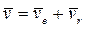 , (13)
, (13)
где 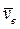 - скорость переносного движения точки P,
- скорость переносного движения точки P, 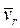 - скорость относительного движения точки P. Соотношение (13) называется теоремой о сложении скоростей. Абсолютное ускорение точки P определим, продифференцировав по времени t соотношение (12):
- скорость относительного движения точки P. Соотношение (13) называется теоремой о сложении скоростей. Абсолютное ускорение точки P определим, продифференцировав по времени t соотношение (12):
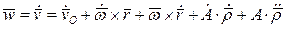 . (14)
. (14)
Обозначая в (14) 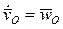 - абсолютное ускорение центра O,
- абсолютное ускорение центра O, 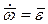 - угловое ускорение твердого тела и учитывая, что
- угловое ускорение твердого тела и учитывая, что 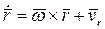 , будем иметь:
, будем иметь:
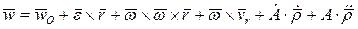 . (15)
. (15)
Следует обратить внимание в (15) на слагаемое 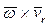 , которое образовалось в результате дифференцирования по времени t переносной скорости
, которое образовалось в результате дифференцирования по времени t переносной скорости 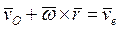 . Покажем, что такое же слагаемое будет иметь место после дифференцирования относительной скорости
. Покажем, что такое же слагаемое будет иметь место после дифференцирования относительной скорости 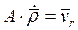 . Для этого обозначим в (15)
. Для этого обозначим в (15) 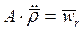 - ускорение относительного движения точки P и умножим слагаемое
- ускорение относительного движения точки P и умножим слагаемое 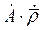 на единичную матрицу
на единичную матрицу 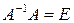 . В результате получим:
. В результате получим:
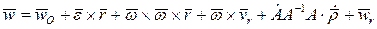 .
.
Замечая, что 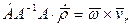 , окончательно будем иметь:
, окончательно будем иметь:
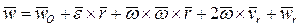 , (16)
, (16)
где 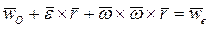 - переносное ускорение,
- переносное ускорение, 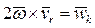 - ускорение Кориолиса. Соотношение (16) называется теоремой о сложении ускорений. Изложенное дает основание сделать важные с точки зрения механики выводы:
- ускорение Кориолиса. Соотношение (16) называется теоремой о сложении ускорений. Изложенное дает основание сделать важные с точки зрения механики выводы:
· Если в переносном движении присутствует вращательная составляющая ( 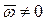 ), то в случае сложного движения точки имеет место ускорение Кориолиса.
), то в случае сложного движения точки имеет место ускорение Кориолиса.
· Множитель «2» в формуле для ускорения Кориолиса отражает тот механический факт, что в образование ускорения Кориолиса переносное и относительное движение вносят одинаковый вклад 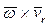 .
.
· Модуль ускорения Кориолиса вычисляется по формуле 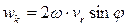 , φ – угол между векторами
, φ – угол между векторами 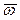 и
и 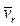 ; направление вектора
; направление вектора 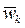 - перпендикуляр к плоскости векторов
- перпендикуляр к плоскости векторов 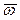 и
и 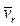 согласно правилу правой тройки (рис 22).
согласно правилу правой тройки (рис 22).
· В динамике сложного движения материальной точки необходимо всегда учитывать возможность возникновения сил инерции, обусловленных ускорением Кориолиса.
Если переносное движение твердого тела является плоским и относительное движение точки происходит в плоскости, параллельной плоскости движения твердого тела, то угловая скорость 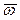 всегда перпендикулярна относительной скорости
всегда перпендикулярна относительной скорости 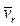 и
и 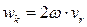 . Для данного случая существует простое правило определения направления ускорения Кориолиса:
. Для данного случая существует простое правило определения направления ускорения Кориолиса:
· Если вектор 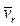 повернуть на 900 в плоскости движения по направлению вращения твердого тела, то этот вектор укажет направление
повернуть на 900 в плоскости движения по направлению вращения твердого тела, то этот вектор укажет направление 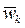 (рис. 23).
(рис. 23).
 | |||||||
 | |||||||
| |||||||
| |||||||
Задача
 | |||||
| |||||
|
Решение
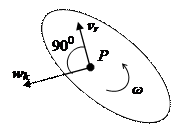
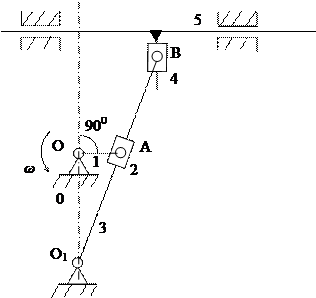
Дадим описание работы механизма станка по заданной схеме (рис. 24). Механизм состоит из шести звеньев: стойки 0, кривошипа 1, кулисного камня 2, кулисы 3, ползушки 4 и суппорта 5. Стойка 0 является в рассматриваемой задаче неподвижным звеном. Кривошип 1 совершает вращательное движение вокруг оси, проходящей через центр O, и является входным звеном.8 Согласно условию задачи, кривошип 1 вращается равномерно с угловой скоростью ω = 4 рад/с. Движение от кривошипа передается кулисе 3 через кулисный камень 2. Кулиса 3 совершает возвратно-качательное движение вокруг оси, проходящей через центр O1. Кулисный камень 2 совершает сложное движение: он движется возвратно-поступательно вдоль кулисы 3 и одновременно вращается вокруг центра O1 вместе с кулисой. Кулиса 3, через ползушку 4, приводит в движение суппорт 5, который является выходным звеном механизма.9 Суппорт 5 совершает возвратно-поступательное движение в горизонтальном направлении. Ползушка 4 совершает сложное движение: она движется возвратно-поступательно в вертикальном направлении относительно суппорта и вместе с суппортом совершает возвратно-поступательное движение в горизонтальном направлении. Все подвижные звенья данного механизма совершают плоское движение.
Обозначим A1 точку A, принадлежащую кривошипу 1, а точку A, принадлежащую кулисе 3, обозначим A3. Тогда, по теореме о сложении скоростей (13), можно записать:
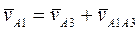 , (17)
, (17)
где 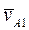 - абсолютная скорость точки A, принадлежащей кривошипу 1,
- абсолютная скорость точки A, принадлежащей кривошипу 1, 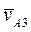 - скорость точки A, принадлежащей кулисе 3 (переносная скорость),
- скорость точки A, принадлежащей кулисе 3 (переносная скорость), 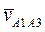 - скорость точки A кривошипа 1 относительно точки A кулисы 3 (относительная скорость). Найдем
- скорость точки A кривошипа 1 относительно точки A кулисы 3 (относительная скорость). Найдем 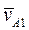 :
: 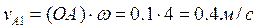 , направление вектора
, направление вектора 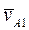 - перпендикуляр к OA в сторону вращения кривошипа 1. Скорости
- перпендикуляр к OA в сторону вращения кривошипа 1. Скорости 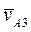 и
и 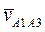 известны только по направлению:
известны только по направлению: 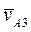 - перпендикуляр к O1B,
- перпендикуляр к O1B, 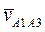 - вдоль O1B. Поэтому, для вычисления величин этих векторов удобно воспользоваться методом векторных планов. Из произвольной точки pv, называемой полюсом плана скоростей, отложим отрезок pva1 произвольной длины, отображающий абсолютную скорость
- вдоль O1B. Поэтому, для вычисления величин этих векторов удобно воспользоваться методом векторных планов. Из произвольной точки pv, называемой полюсом плана скоростей, отложим отрезок pva1 произвольной длины, отображающий абсолютную скорость 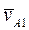 (рис. 25). Согласно векторному уравнению (17) через точку a1 проведем прямую, параллельную O1B (направление скорости
(рис. 25). Согласно векторному уравнению (17) через точку a1 проведем прямую, параллельную O1B (направление скорости 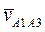 ) и через точку pv – прямую, перпендикулярную O1B (направление
) и через точку pv – прямую, перпендикулярную O1B (направление 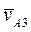 ). На пересечении этих прямых получим точку a3. Так как треугольник векторов прямоугольный и подобный треугольнику OO1A, то
). На пересечении этих прямых получим точку a3. Так как треугольник векторов прямоугольный и подобный треугольнику OO1A, то 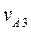 и
и 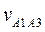 вычислим по теореме Пифагора:
вычислим по теореме Пифагора:
 | |||||
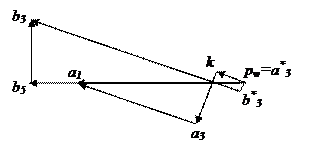 | |||||
| |||||
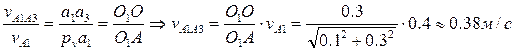 ;
;
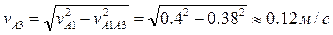 . Угловая скорость кулисы 3:
. Угловая скорость кулисы 3: 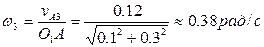 .
.
Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно (13) имеем:
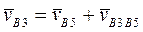 , (18)
, (18)
где 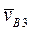 - абсолютная скорость точки B, принадлежащей кулисе 3,
- абсолютная скорость точки B, принадлежащей кулисе 3, 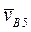 - абсолютная скорость точки B, принадлежащей суппорту 5 (переносная скорость),
- абсолютная скорость точки B, принадлежащей суппорту 5 (переносная скорость), 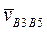 - скорость точки B, принадлежащей кулисе 3 относительно точки B, принадлежащей суппорту 5. Определим
- скорость точки B, принадлежащей кулисе 3 относительно точки B, принадлежащей суппорту 5. Определим 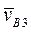 :
: 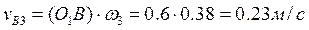 , направление
, направление 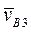 - перпендикуляр к O1B. Скорости
- перпендикуляр к O1B. Скорости 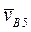 и
и 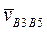 известны только по направлению, поэтому их величины определим, построив векторный план. Отложим от точки pv в направлении pva3 отрезок
известны только по направлению, поэтому их величины определим, построив векторный план. Отложим от точки pv в направлении pva3 отрезок 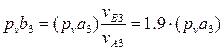 , отображающий на плане скорость
, отображающий на плане скорость 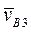 (рис. 25). Через точку b3, согласно (18), проведем прямую по направлению скорости
(рис. 25). Через точку b3, согласно (18), проведем прямую по направлению скорости 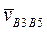 и замкнем треугольник прямой, проведенной в направлении скорости
и замкнем треугольник прямой, проведенной в направлении скорости 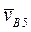 . На пересечении этих прямых отметим точку b5. Так как полученный треугольник – прямоугольный и подобный верхнему треугольнику, то то
. На пересечении этих прямых отметим точку b5. Так как полученный треугольник – прямоугольный и подобный верхнему треугольнику, то то 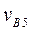 и
и 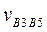 вычислим по теореме Пифагора:
вычислим по теореме Пифагора:
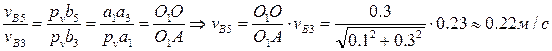 ,
,
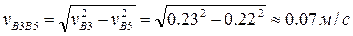 .
.
Таким образом, скорость суппорта 5 в положении, указанном на рис. 24, равна 0.22 м/с и направлена влево. Полученный результат соответствует исходным данным: действительно, согласно положению механизма на схеме, крайнее правое положение суппортом уже пройдено и он движется в обратном направлении.
Определим ускорения звеньев механизма. По теореме о сложении ускорений (16) можно записать:
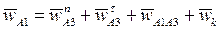 , (19)
, (19)
где 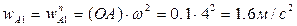 (
( 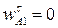 , т.к.
, т.к. 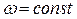 );
); 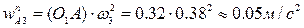 ,
, 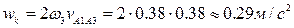 . Таким образом, в уравнении (19) присутствуют два неизвестных по величине ускорения; для их вычисления воспользуемся методом векторных планов. Отложим от полюса плана ускорений pw отрезок pwa1, изображающий ускорение точки A кривошипа 1 (рис. 26). Для удобства вычислений длину этого отрезка примем равной 40 мм. Тогда масштаб плана ускорений
. Таким образом, в уравнении (19) присутствуют два неизвестных по величине ускорения; для их вычисления воспользуемся методом векторных планов. Отложим от полюса плана ускорений pw отрезок pwa1, изображающий ускорение точки A кривошипа 1 (рис. 26). Для удобства вычислений длину этого отрезка примем равной 40 мм. Тогда масштаб плана ускорений 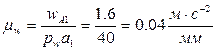 . Переведем в отрезки известные нам по величине ускорения:
. Переведем в отрезки известные нам по величине ускорения: 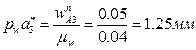 ,
, 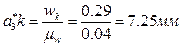 . Так как отрезок pwa*3 мал, пренебрежем его длиной, и будем считать, что точки pw и a*3 совпадают. Направление отрезка
. Так как отрезок pwa*3 мал, пренебрежем его длиной, и будем считать, что точки pw и a*3 совпадают. Направление отрезка 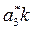 , изображающего ускорение Кориолиса, определим, повернув отрезок
, изображающего ускорение Кориолиса, определим, повернув отрезок 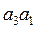 , изображающий относительную скорость
, изображающий относительную скорость 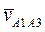 , (рис. 25) на 900 в направлении вращения кулисы 3. Замыкая векторный многоугольник направлениями ускорений
, (рис. 25) на 900 в направлении вращения кулисы 3. Замыкая векторный многоугольник направлениями ускорений 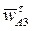 и
и 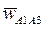 , в соответствии с уравнением (19) получим точку
, в соответствии с уравнением (19) получим точку 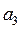 . Тогда отрезку
. Тогда отрезку 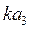 будет соответствовать относительное ускорение
будет соответствовать относительное ускорение 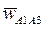 , а отрезку
, а отрезку 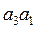 - тангенциальное ускорение
- тангенциальное ускорение 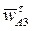 точки A, принадлежащей кулисе 3. Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно (16) имеем:
точки A, принадлежащей кулисе 3. Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно (16) имеем:
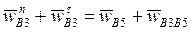 , (20)
, (20)
где 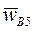 - ускорение суппорта 5,
- ускорение суппорта 5, 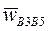 - ускорение точки B кулисы 3 относительно точки B суппорта 5. В данном случае
- ускорение точки B кулисы 3 относительно точки B суппорта 5. В данном случае 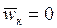 , так как переносное движение суппорта – поступательное. Нормальное ускорение
, так как переносное движение суппорта – поступательное. Нормальное ускорение 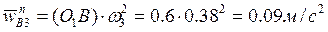 , отображающий это ускорение отрезок
, отображающий это ускорение отрезок 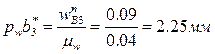 . Отрезок b*3b3, отображающий тангенциальное ускорение
. Отрезок b*3b3, отображающий тангенциальное ускорение 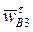 , найдем из соотношения:
, найдем из соотношения: 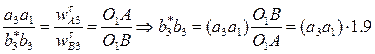 . Замыкая векторный многоугольник направлениями ускорений
. Замыкая векторный многоугольник направлениями ускорений 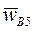 и
и 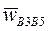 в соответствии с уравнением (20) получим точку b5 (рис. 26). Отрезок pwb5 отображает на плане ускорение суппорта 5. Длина этого отрезка – 55 мм, следовательно
в соответствии с уравнением (20) получим точку b5 (рис. 26). Отрезок pwb5 отображает на плане ускорение суппорта 5. Длина этого отрезка – 55 мм, следовательно 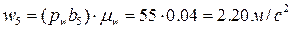 .
.
Таким образом, ускорение суппорта в положении механизма, изображенном на рис. 24, равно 2.20 м/c2 и направлено в ту же сторону, что и вектор скорости суппорта. Это означает, что в данный момент времени суппорт ускоряется. Планы скоростей и ускорений, изображенные на рис. 25 и рис. 26 соответственно, дают полную информацию о скоростях и ускорениях звеньев механизма в заданном на рис. 24 положении. Для того чтобы получить векторные планы в другом положении механизма, необходимо заново выполнить все приведенные вычисления.
Вопросы для проверки усвоения материала
1) Дайте определение понятию «абсолютно твердое тело».
2) Чему равно число степеней свободы твердого тела в трехмерном пространстве?
3) В чем разница между понятиями перемещения и движения твердого тела?
4) Назовите простейшие перемещения твердого тела.
5) Что такое матрица поворота твердого тела? Перечислите основные свойства матрицы поворота.
6) Запишите матрицы элементарных поворотов твердого тела.
7) Как задается поступательное перемещение твердого тела?
8) Как задается произвольное перемещение твердого тела?
9) Что такое угловая скорость твердого тела?
10) Как вычислить угловую скорость твердого тела, зная матрицу поворота A(t)?
11) Как вычислить абсолютную скорость произвольной точки твердого тела, зная матрицу поворота A(t) и вектор переноса RO(t)?
12) Что такое угловое ускорение твердого тела?
13) Как вычислить абсолютное ускорение произвольной точки твердого тела, зная матрицу поворота A(t) и вектор переноса RO(t)?
14) По каким траекториям движутся точки твердого тела относительно неподвижной оси вращения?
15) Что такое плоское движение твердого тела?
16) Какие независимые перемещения твердого тела имеют место в случае плоского движения?
17) Почему в случае плоского движения твердого тела можно оперировать угловыми скоростью и ускорением как скалярными величинами?
18) Что такое сложное движение точки? Сформулируйте теоремы о сложении скоростей и о сложении ускорений.
