Произвольное движение твердого тела

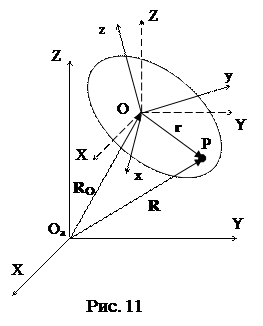
Пусть теперь система координат OXYZ перемещается относительно неподвижной (абсолютной) системы координат O_aXYZ таким образом, что соответствующие оси всегда остаются параллельными: OX // O_aX, OY // O_aY, OZ // O_aZ (рис. 11). Система координат Oxyz, по-прежнему, жестко связана с твердым телом. Тогда положение некоторой точки P тела, совершающего произвольное перемещение, определится из соотношения:

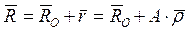, (2)

где 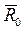- радиус-вектор центра O в неподвижной системе координат, 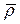- радиус-вектор точки P в системе координат Oxyz.

Теперь, если задать 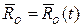и 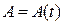, то будет задано движение твердого тела в абсолютной системе координат.

Задача

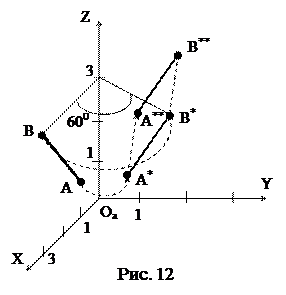
Определить конечное положение стержня AB из предыдущей задачи, если стержень после поворота на угол θ = 60⁰ вокруг оси OZ совершил поступательное перемещение .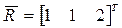

Решение

Введем абсолютную систему координат O_aXYZ так, чтобы в начальном положении системы координат O_aXYZ и OXYZ совпадали. Тогда конечные положения точек A и B стержня будут получены из соотношений:

, .

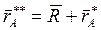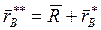Выполняя вычисления, получим:

, .

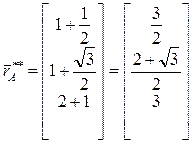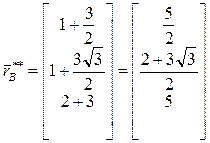Начальное, промежуточное и конечное положения стержня, а также его перемещения изображены на рис. 12.

2.4. Скорость точки твердого тела в случае его произвольного движения

Пусть задан радиус-вектор некоторого центра O твердого тела 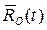и матрица поворота A(t). Тогда скорость любой точки P, принадлежащей этому телу определится из соотношения:

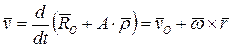, (3)

где 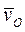- абсолютная скорость центра O, 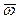- угловая скорость твердого тела. Координаты вектора 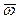в системе координат O_aXYZ определяются как элементы кососимметрической матрицы5

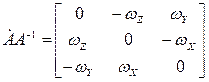. (4)

Скорость центра 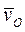и угловая скорость 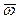являются величинами, общими для всего твердого тела. Согласно (3), с их помощью можно вычислить скорость любой точки твердого тела относительно неподвижного начала отсчета.

Задача

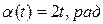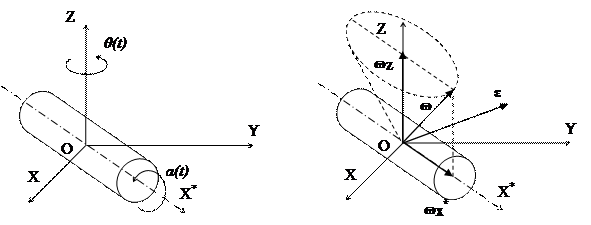
Вал, на котором укреплена зенитная пушка, вращается вокруг своей оси OX^* по закону и одновременно поворачивается вокруг оси OZ неподвижной системы координат OXYZ по закону 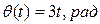(рис. 13). Определить угловую скорость вала.

		Рис. 14
		Рис. 13

Решение

По условию задачи, вал вращается вокруг неподвижной точки O. Найдем матрицу поворота вала:

.

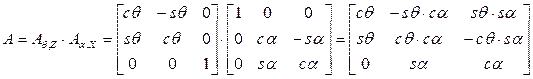Вектор угловой скорости вала 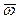найдем согласно (4). Для этого выполним следующие вычисления:

; .

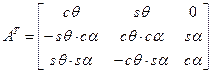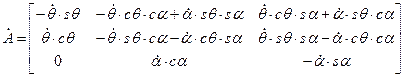Учитывая, что 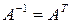, получаем:

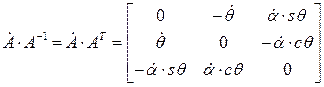, откуда .

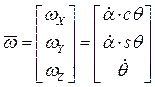Модуль вектора угловой скорости: 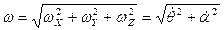. Подставляя исходные данные 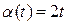, 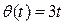в полученные соотношения, окончательно будем иметь:

, .

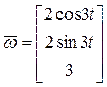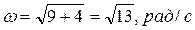Таким образом, вектор угловой скорости вала имеет постоянную величину 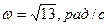и вращается вокруг оси OZ по закону 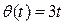(рис. 14).

2.5. Ускорение точки твердого тела в случае его произвольного движения

Ускорение точки P, принадлежащей твердому телу, вычисляется в соответствии с соотношением:

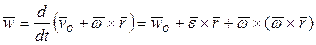, (5)

где 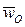- ускорение центра O, 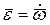- угловое ускорение твердого тела. Слагаемое 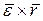называют вращательным, а 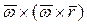- осестремительным ускорением. Ускорение центра 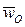и угловое ускорение 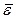являются величинами, общими для всего твердого тела.

Задача

Вычислить угловое ускорение вала из задачи п. 2.4.

Решение

Угловое ускорение найдем, продифференцировав по времени t вектор угловой скорости:

.

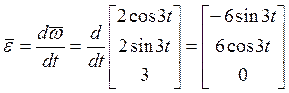Модуль углового ускорения: 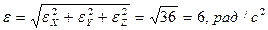. Таким образом, угловое ускорение вала постоянно по величине, находится в плоскости OXY нормально к 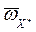и вращается вокруг оси OZ вместе с вектором 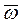(рис. 14).