Понятие экономических рядов динамики. Сглаживание временных рядов

Динамические процессы, происходящие в экономических системах, чаще всего проявляются в виде ряда последовательно расположенных в хронологическом порядке значений того или иного показателя, который в своих изменениях отражает ход развития изучаемого явления в экономике. Предварительно рассмотрим ряд понятий.

Последовательность наблюдений одного показателя (признака), упорядоченных в зависимости от последовательно возрастающих или убывающих значений другого показателя (признака), называют динамическим рядом, или рядом динамики.

Если в качестве признака, в зависимости, от которого происходит упорядочение, выступает время, то такой динамический ряд называется временным рядом.

Эконометрические модели можно строить, используя два типа исходных данных, характеризующих:

­ совокупность различных объектов в определенный момент (период) времени;

­ один объект за ряд последовательных моментов (периодов) времени.

Модели, построенные по данным 1-го типа, называются пространственными моделями, по данным второго типа - моделями временных рядов

Время, прошедшее от начального момента наблюдения до конечного, называют длиной временного ряда, а значения показателя в каждый конкретный момент времени - уровнями временного ряда.

Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно разделить на 3 группы:

­ факторы, формирующие тенденции ряда;

­ факторы, формирующие циклические колебания ряда;

­ случайные факторы.

При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы.

Если во временном ряду проявляется длительная тенденция изменения экономического показателя, то говорят, что имеет место тренд (рис.5.1а).

Изучаемый показатель может быть подвержен циклическим колебаниям.

Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельхозпродукты) (рис.5.1б).

Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется под воздействием случайной компоненты (например, изменение курса американского доллара по отношению к рублю) (рис. 5.1в).

Рис.5 Основные компоненты временного ряда:

а)- возрастающая тенденция; б) - сезонная; в) – случайная компонента.

Если модель является временным рядом, представленным как сумма трендовой, циклической и случайной компонент, то такая модель называется аддитивной моделью временного ряда.

Если в модели временный ряд представлен как произведение перечисленных компонент, то такая модель называется мультипликативной моделью временного ряда.

Для статического анализа одномерных временных рядов экономических показателей вида: y₁,у₂,…у_n вычисляют ряд величин:

- абсолютный прирост , который показывает величину изменения показателя за определенный интервал времени;

- средний абсолютный прирост: , т.е. прирост в единицу времени;

-коэффициент роста для t-го периода ,

-коэффициент прироста .

На практике часто применяют показатель темпа роста и темпа прироста:

, где Т - темп роста для t-го периода;

, где Т - темп прироста для t-го периода.

Важной характеристикой временного ряда является также средний уровень ряда:

, где n число наблюдений

Предварительный анализ временных рядов экономических показателей заключается в основном в выявлении и устранении аномальных значений уровней ряда, а также в определении наличия тренда в исходном временном ряде.

Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и оказывает существенное влияние на значения основных характеристик временного ряда.

Для выявления аномальных уровней временных рядов используются методы, рассчитанные для статистических совокупностей, например, метод Ирвина предполагает использование следующей формулы:

; t = 2,3, …, n.

где ; .

Расчетные значения , и т.д. сравниваются с табличными значениями критерия Ирвина , и если какое-то значение оказывается больше табличного, то соответствующее значение у 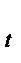уровня ряда считается аномальным.

Для определения наличия тренда в исходном временном ряду применяют ряд методов, в частности метод проверки разностей средних уровней. Реализация этого метода состоит из 4-х этапов:

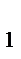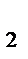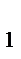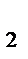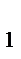- на 1-м этапе исходный временной ряд у ,у ,у …у разбивается на две, примерно равные по числу уровней, части: n и n ( n 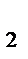+ n = n);

­ на 2-м этапе для каждой из частей вычисляются средние значения и дисперсии:

; ; ;

.

3-й этап заключается в проверке равенства дисперсий обеих частей с помощью F-критерия Фишера:

Если расчетное значение F меньше F , то переходят к 4-му этапу. Если F F , то делается вывод, что данный метод для определения наличия тренда ответа не дает.

На 4-м этапе определяется расчетное значение критерия Стьюдента по формуле:

, где .

Если t <t с заданным уровнем значимости , то тренда нет, в противном случае тренд есть.

Чтобы более четко выявить тенденцию развития исследуемого процесса производят сглаживание (выравнивание) временных рядов.

Сглаживания временных рядов можно осуществлять аналитическими или механическими методами.

Суть аналитических методов заключается в построении кривой, проходящей между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний.

Суть методов механического сглаживания заключается в следующем: берется несколько первых уровней временного ряда, образующих интервал сглаживания, и для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженное значение и т.д.

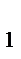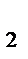Простейшим методом механического сглаживания является метод простой скользящей средней. Согласно этому методу для временного ряда у ,у ,у …у определяется интервал сглаживания m (m<n). Для первых m уровней временного ряда вычисляется их средняя арифметическая. Затем интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление средней арифметической и т.д.

Для вычисления сглаженных уровней ряда `у_t применяется формула:

, t >p, где .

В результате этой процедуры получаются n-m+1 сглаженных значений уровней ряда; при этом первые р и последние р-уровней ряда теряются.