Обобщённый метод наименьших квадратов. Гомоскедастичность и гетероскедастичность

При построении модели, например, линейного вида 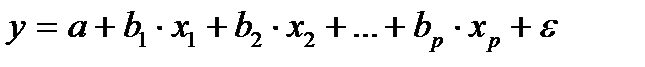случайная величина e представляет собой ненаблюдаемую величину. Для разных спецификаций модели разности 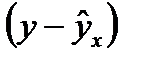между теоретическими и фактическими значениями могут меняться. В задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений e_i т.е. остаточных величин. После построения уравнения регрессии проводится проверка наличия у оценок e_i некоторых свойств. Эти свойства оценок, полученных МНК, имеют очень важное практическое значение в использовании результатов регрессии и корреляции.

Коэффициенты регрессии b­_i, найденные на основе системы нормальных уравнений и представляющие собой выборочные оценки характеристики силы связи, должны обладать свойством несмещености. Несмещенность оценки означает, что математическое ожидание остатков равно нулю.

Это означает, что найденный параметр регрессии b­_i, можно рассматривать как среднее значение возможных значений коэффициентов регрессии с несмещенными оценками остатков.

Для практических целей важны не только несмещенность, но и эффективность оценок. Оценки считаются эффективными,если они характеризуются наименьшей дисперсией.

Для того, чтобы доверительные интервалы параметров регрессии были реальными, необходимо, чтобы оценки были состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки.

Исследования остатков e_i предполагают проверку наличия следующих пяти предпосылок МНК:

­ случайный характер остатков;

­ нулевая средняя величина остатков, не зависящая от х_i;

­ гомоскедастичность–дисперсия каждого отклонения e_i одинакова для всех значений х;

­ отсутствие автокорреляции остатков. Значения остатков e_i распределены независимо друг от друга;

­ остатки подчиняются нормальному распределению.

Если распределение случайных остатков e_i не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Прежде всего, проверяется случайный характер остатков e_i.

Строится график зависимости остатков e_i от теоретических значений результативного признака (рис.3.1)

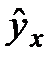
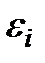
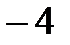
Рис 3.1.Зависимость случайных остатков e_i. от теоретических значений у_x

Если на графике получена горизонтальная полоса распределения остатков, то остатки представляют собой случайные величины и МНК оправдан, теоретические значения у_x хорошо аппроксимируют фактические значения у.

Возможны следующие случаи: если e_i. зависит от у_x то:

­ остатки e_i. не случайны (рис.3.2а)

­ остатки e_i. не имеют постоянной дисперсии (рис.3.2в)

­ остатки e_i. носят систематический характер (рис. 3.2б).

В этих случаях (а,б,в) необходимо либо применить другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки e_i не будут случайными величинами.

Вторая предпосылка означает равенство нулю средней величины остатков:

.

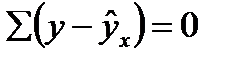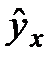
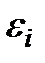
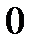
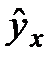
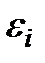
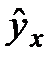
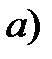
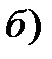
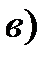
Рис 3.2. Зависимость случайных остатков e_i от теоретических значений у_x

В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора х_j остатки e_i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Примеры гетероскедастичности приведены на рис.3.3.

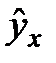
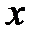
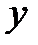
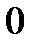
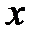
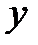
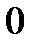
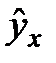
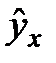
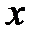
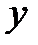
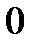
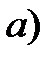
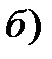
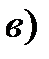
Рис3.3. Примеры гетероскедастичности

Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков от теоретических значений результативного признака у_x.

Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.

При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения e_i распределены независимо друг от друга.

Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.

Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t и F. Вместе с тем оценки регрессии, найденные с применением МНК, обладает хорошими свойствами даже при отсутствии нормального распределения остатков.

При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы и т.д.

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный МНК заменять обобщенным МНК.

Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии

Предположим, что среднее значение остаточных величин равно нулю:

.

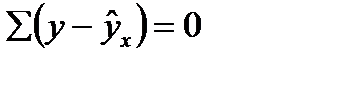А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине k_i, т.е. :

,

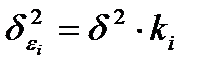где 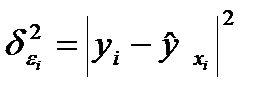- дисперсия ошибки при конкретном i-м значении фактора,

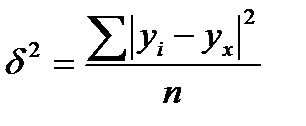- постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков,

k_i - коэффициент пропорциональности, меняющийся с изменением величины фактора.

Для уравнения

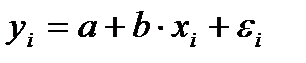при 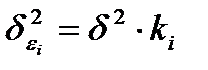модель примет вид: .

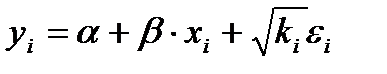В этой модели остатки гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками:

.

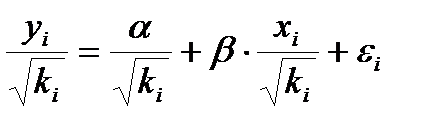Полученное уравнение регрессии представляет собой взвешенное уравнение регрессии, в которой переменные : у и х взяты в весами .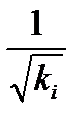

Оценка параметров нового уравнения с преобразованием переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений

.

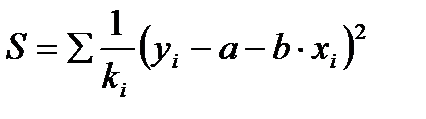Получаем следующую систему нормальных уравнений

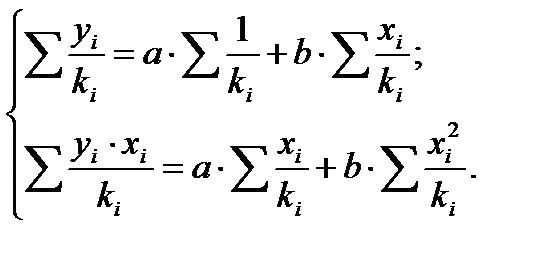
Коэффициент регрессии 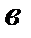можно определить как:

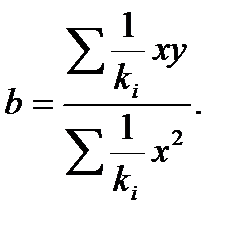
При обычном МНК формула для определения b будет иметь вид:

.

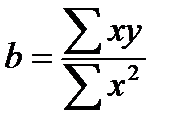Таким образом, при использовании обобщенного МНК, с целью корректировки гетероскедастичности, коэффициент b представляет собой взвешенную величину по отношению к обычному МНК с весами 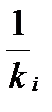. Аналогичный подход возможен и для множественной регрессии.