Оценка корреляции для нелинейной регрессии

Оценка тесноты корреляционной зависимости в случае нелинейной регрессии производится с помощью индекса корреляции (R):

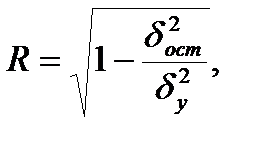
где , , ,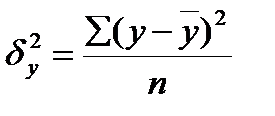

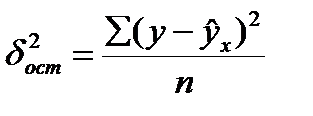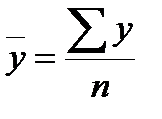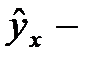значения результативного признака, рассчитанные по уравнению регрессии.

Величина данного показателя находится в границах: 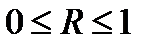, чем она ближе к единице, тем теснее связь рассматриваемых признаков, тем надежнее найденное уравнение регрессии.

Следует помнить, что если для линейной зависимости имеет место равенство: 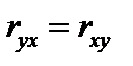, то при криволинейной зависимости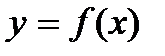 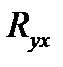не равен .

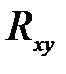Величина R² называется индексом детерминации.

Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:

,

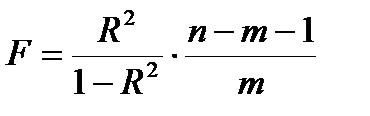где R²- индекс детерминации;

n - число наблюдений;

m - число параметров при переменных х.

Индекс детерминации 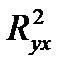можно сравнивать с коэффициентом детерминации 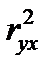для обоснования возможности применения линейной функции.

Если величина 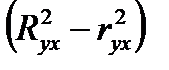не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия между 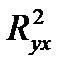и r²_yx, вычисленных по одним и тем же исходным данным, через t - критерий Стьюдента:

,

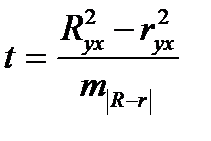где ,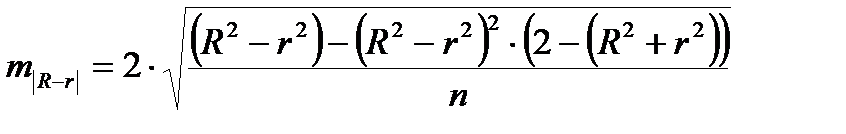

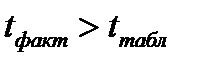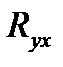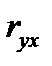Если , то различия между и существенны и замена нелинейной регрессии линейной - невозможна. Практически, если 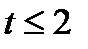, то различия между 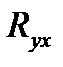и 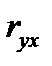несущественны, и, следовательно, возможно применение линейной регрессии.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. 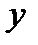и 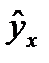. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

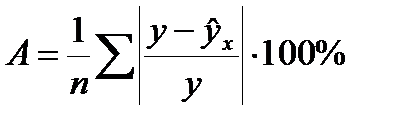
Существует и другая формула определения средней ошибки аппроксимации:

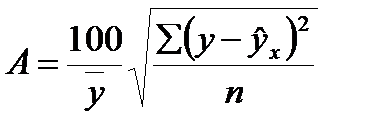, где .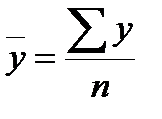

Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.

Возможность построения нелинейных моделей, как с помощью их приведения к линейному виду, так и путем использования нелинейной регрессии, значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя.

Возникает вопрос: с чего начать - с линейной зависимости или с нелинейной, и если с последней, то, какого типа.

Если ограничиться парной регрессией, то можно построить график наблюдений у и х и принять решение. Однако очень часто несколько разных нелинейных функцией приблизительно соответствуют наблюдениям, если они лежать на некоторой кривой. А в случае множествен6ной регрессии невозможно даже построить график.

При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной процедура выбора достаточно проста. Наиболее разумным является оценивание регрессии на основе всех вероятных функций, и выбор функции, в наибольшей степени объясняющей изменения зависимой переменной. Если для одной модели коэффициент R² значительно больше, чем для другой, то вы сможете сделать оправданный выбор без особых раздумий, однако, если значения R² для двух моделей приблизительно равны, то проблема выбора существенно усложняется.

В этом случае следует использовать стандартную процедуру, известную под названием теста Бокса – Кокса.

Если необходимо сравнить модели с использованием у и lny в качестве зависимой переменной, то можно использовать вариант теста, разработанный Полом Зарембкой. Процедура включает следующие шаги:

1. Вычисляется среднее геометрическое значений у в выборке, (оно совпадает с экспонентой среднего арифметического lny):

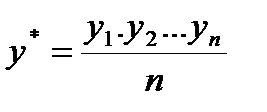
2. Пересчитываются наблюдения у, т.е. они делятся на это значение, то есть

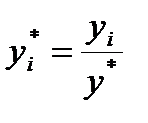
3. Оценивается регрессия для линейной модели с использованием у^*_i вместе y_i и для логарифмической модели с использованием ln(y^*_i) вместо ln(y_i). Теперь значения суммы квадратов отклонений для двух регрессий сравнимы, и, следовательно, модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.