Условия равновесия пространственной системы сходящихся сил

Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю:

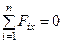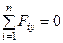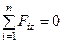; ; , (21)

В случае плоской системы сходящихся сил одну из осей координат, обычно 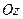, выбирают перпендикулярной силам, а две другие оси – соответственно в плоскости сил. Для равновесия плоской системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координатных осей, лежащих в плоскости сил, были равны нулю:

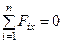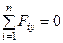; , (22)

Условия равновесия пространственной системы параллельных сил

Направим ось 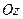параллельно силам: для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю:

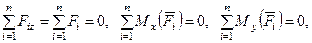(23)

Условия равновесия плоской системы сил

Расположим ос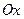и и 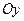в плоскости действия сил.

Условия равновесия плоской системы сил в первой форме: для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю:

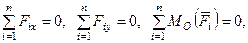(24)

Для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю:

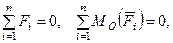(25)

Теорема о трех моментах (вторая форма условий равновесия): для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю:

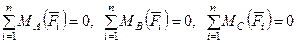. (26)

Третья форма условий равновесия: для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю и алгебраическая сумма проекций этих сил на какую-либо ось плоскости, не перпендикулярную прямой, проходящей через две моментные точки, также была равна нулю, т.е.

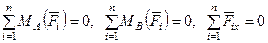. (27)

Центр тяжести твердого тела

Центр параллельных сил

Пусть на тело действует система параллельных сил 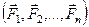. Такая система имеет равнодействующую 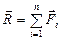(если главный вектор отличен от нуля), линия действия которой проходит всегда через одну и ту же точку тела 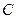, независимо от ориентации сил. Эта точка называется центром параллельных сил, ее положение в пространстве определяется радиус-вектором :

,

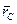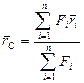где 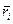– радиус-вектор точки приложения силы .

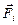Координаты 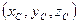центра параллельных сил определяется по формулам:

, , .

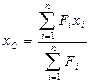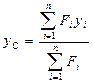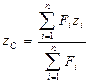Центр тяжести твердого тела – это центр параллельных сил, представляющих силы тяжести материальных частиц, из которых состоит тело. Если тело находится на поверхности Земли и его размеры малы по сравнению с радиусом Земли, можно считать, что линии действия сил тяжести параллельны, а их величины зависят только от объема материальных частиц, плотности материала и ускорения свободного падения.

Формулы для нахождения центра тяжести твердого тела:

, , , ,

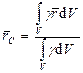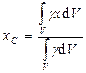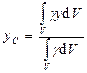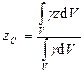где 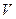– объем тела, 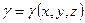– удельный вес, 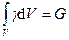– вес тела.