Приведение системы сил к простейшей системе. Условия равновесия

Лемма о параллельном переносе сил: силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы.

Этот процесс замены силы силой и парой сил называют приведением силы к заданному центру.

Приведение произвольной системы сил к силе и паре сил (теорема Пуансо): любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил. Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру:

~ ,

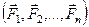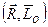Величина

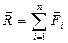(16)

называется главным вектором системы сил – это вектор, равный векторной сумме этих сил.

Вектор

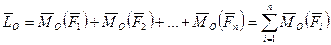. (17)

называется главным моментом системы сил относительно центра 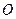, он равен сумме векторных моментов всех сил системы относительно центра :

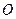Равновесие пар сил

Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил:

.

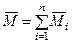Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю. Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил на каждую из трех координатных осей была равна нулю:

Отсюда:

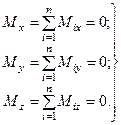(18)

В том случае, когда пары сил действуют на твердое тело, находясь в одной плоскости, их можно заменить одной эквивалентной парой сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил:

.

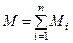Для равновесия таких пар сил необходимо и достаточно, чтобы алгебраический момент эквивалентной им пары сил был равен нулю, т.е. для равновесия пар сил, действующих на твердое тело в одной плоскости, необходимо и достаточно, чтобы сумма алгебраических моментов этих пар сил была равна нулю.

Условия равновесия произвольной системы сил в векторной форме

Векторные условия равновесия произвольной системы сил: для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю. Иначе: для того чтобы 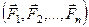~0, необходимы и достаточны условия:

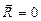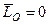, или 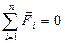, 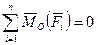. (19)

Условия равновесия пространственной системы сил в аналитической форме

Для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

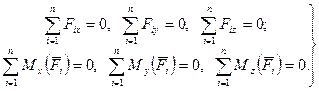. (20)