Пара сил и алгебраический момент пары сил

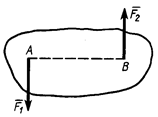Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 5).

Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.

Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил.

Плечом пары сил 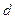называют кратчайшее расстояние между линиями действия сил пары.

Алгебраический момент пары обозначим 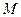или 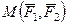. Согласно определению,

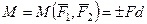. (6)

Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке.

Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности двух пар сил: пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.

Следствия теоремы:

а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;

б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Теорема об эквивалентности двух пар сил, расположенных в одной плоскости: действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость.

Векторным моментом 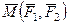пары сил 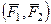назовем вектор, числовое значение которого равно произведению силы пары на ее плечо. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил так, чтобы с его направления можно было видеть стремление пары сил вращать тело против часовой стрелки (рис. 6).

,

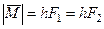где 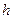– плечо пары сил.

Теорема об эквивалентности пар сил: две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.

Теорема о сумме моментов сил пары сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора точки и равна векторному моменту этой пары сил, т.е. для пары сил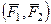

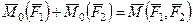, (7)

где 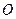– любая точка.

Теорема о сложении пар: две пары сил, действующие на одно и то же тело и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил.

Для пар сил, расположенных в одной плоскости, теорема об их сложении формулируется так: пары сил, действующие на твердое тело и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, т. е.

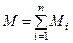. (8)

Аксиомы статики

При формулировке аксиом предполагаем, что на твердое тело или материальную точку действуют силы, которые указаны в соответствующей аксиоме.

I. Аксиома о равновесии системы двух сил. Для равновесия системы двух сил, приложенных к точкам твердого тела (рис. 7), 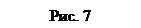необходимо и достаточно, чтобы эти силы были равны пол модулю и действовали вдоль одной прямой, проходящей через точки их приложения, в противоположных направлениях.

II. Аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю. Если на твердое тело действует система сил, то к ней можно добавить (отбросить) систему сил, эквивалентную нулю. Полученная после добавления (отбрасывания) новая система сил является эквивалентной первоначальной системе сил. Под действием заданной системы сил и новой, полученной после добавления (отбрасывания) равновесной системы сил, тело будет двигаться (или находиться в покое) совершенно одинаково при прочих равных условиях.

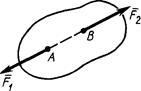
III. Аксиома параллелограмма сил. Две силы, действующие в одной точке твердого тела или на одну материальную точку, можно заменить одной равнодействующей силой, равной по модулю и направлению диагонали параллелограмма, построенного на заданных силах (рис. 8). Очевидно, справедливо и обратное. Одну силу, приняв за равнодействующую, можно разложить по правилу параллелограмма на две составляющие силы.

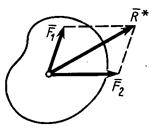
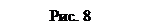Замену двух сил одной равнодействующей силой по правилу параллелограмма называют векторным сложением этих сил. Векторное сложение сил 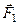и 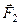математически выражают так:

.

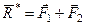Модуль 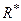равнодействующей силы как векторную сумму сил вычисляют по формуле диагонали параллелограмма

.

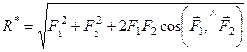IV. Аксиома о равенстве сил действия и противодействия. Всякой силе действия есть равная, но противоположная сила противодействия. По отношению к двум материальным точкам эта аксиома утверждает, что силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и действуют вдоль одной прямой, проходящей через взаимодействующие точки.

V. Аксиома связей. Связью для твердого тела или материальной точки называют материальные объекты (тела и точки), которые ограничивают свободу перемещения рассматриваемого твердого тела или материальной точки. Аксиома связей утверждает, что всякую связь можно отбросить и заменить силой, реакцией связей (в простейшем случае) или системой сил (в общем случае).

Приведем примеры связей и их замены силами реакций связей. Если связью для твердого тела (рис. 9,а) является абсолютно гладкая поверхность другого тела, то сила реакции такой поверхности, если соприкосновение происходит в одной точке, направлена по нормали к общей касательной соприкасающихся поверхностей тел независимо от сил, приложенных к рассматриваемому телу (рис. 9,б). Сила реакции связи 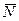направлена в сторону, противоположную направлению, в котором связь препятствует перемещению рассматриваемого тела.

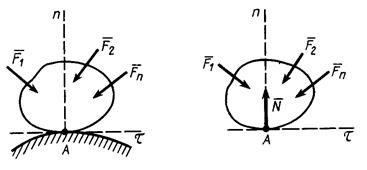
а) б)

Рис. 9

Числовое значение силы реакции при равновесии определяется приложенными к телу силами, которые в отличие от сил реакций связей часто называют активными силами.

Неизвестную по модулю и направлению силу реакции создают цилиндрический (плоский) и шаровой шарниры. Пусть имеем балку АВ, находящуюся в равновесии под действием силы 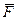и закрепленную на одном конце с помощью цилиндрического шарнира А, а на другом – катковой опоры В (рис. 10, а). Цилиндрическим шарниром называют устройство, позволяющее балке поворачиваться в плоскости вокруг оси, перпендикулярной этой плоскости. Устройство катковой опоры ясно из рисунка. На рис. 10,б показана та же балка после освобождения от связей. Сила реакции катковой опоры направлена по нормали к плоскости движения катков. Неизвестная по модулю и направлению реакция цилиндрического шарнира разложена на две составляющие 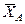и 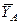, предположительно направленные в положительном направлении осей координат.

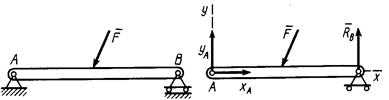
а) б)

Рис. 10

В случае шарового шарнира силу реакции раскладывают на три составляющие, параллельные осям координат.

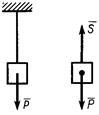
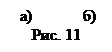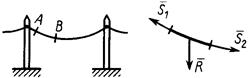
Гибкие связи (канаты, тросы, нити) дают силы реакции связей (силы натяжения), направленные по касательной к гибкой связи. На рис. 11,а,б сила натяжения нити 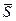заменяет действие нити на груз. На рис. 12,а,б показаны силы натяжения провода в сечениях А и В, действующих на часть провода АВ.

а) б)

Рис. 12

Жесткая заделка. Запрещает любое поступательное перемещение тела, в общем случае ее реакция состоит из произвольно направленной силы реакции заделки и момента заделки. При решении задач их раскладывают на составляющие по осям координат.

VI. Аксиома затвердевания. Если деформируемое тело находится в равновесии, то равновесие его без изменения системы приложенных сил не нарушится от наложения на точки тела дополнительных связей, включая превращение деформируемого тела в абсолютно твердое.

ЛЕКЦИЯ № 2

Простейшие теоремы статики

Теорема о переносе силы вдоль линии действия: Действие силы на твердое тело не изменится от переноса

Теорема о трех силах: если твердое тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таких трех сил пересекаются в одной точке. Обратная теорема неверна, т.е. если линии действия трех сил пересекаются в одной точке, то такая система сил не обязательно является равновесной.

Системой сходящихся сил (или пучком сил) называют такую систему сил, линии действия которых пересекаются в одной точке – центре пучка. Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.

Таким образом, система 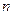сходящихся сил эквивалентна одной силе 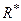, которая и является равнодействующей этой системы сил.

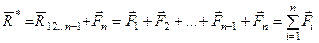. (9)

Проецируя векторы векторного равенства на прямоугольные оси координат, получим:

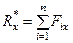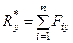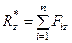; ; . (10)

По проекциям определяем модуль равнодействующей силы и косинусы углов ее с осями координат по формулам

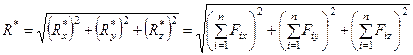;(11)

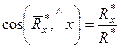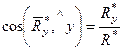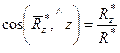, , ; (12)

Теорема о моменте равнодействующей силы (теорема Вариньона): векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки:

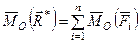. (13)

Теорема Вариньона относительно оси 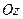: момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.

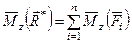, (14)

Для случая плоской системы сил, если точку 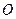выбрать в плоскости действия сил, получаем теорему Вариньона для плоской системы сил: алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.

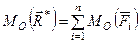. (15)