Раздел 8. Вероятность и статистика

Теория вероятностей представляет собой раздел математики, изучающий закономерности случайных явлений. Он зародился в 17 веке из анализа азартных игр, стрельбы, страхового дела, взвешивания. В настоящее время теория вероятностей используется при планировании и организации производства, организации технологических процессов, в теоретической физике, а также в военном деле, экономике, теории массового обслуживания.

Параллельно с теорией вероятностей развивалась и математическая статистика – раздел математики, также зародившийся в 17 веке, который занимается разработкой научно обоснованных методов сбора статистических данных и их обработки. Математическая статистика опирается на теорию вероятностей, поскольку также изучает случайные явления, но решает, в некотором смысле, обратные ей задачи. Если теория вероятностей исследует явления, заданные полностью их моделью и выявляет ещё до опыта те статистические закономерности, которые будут иметь место после его проведения, то в математической статистике вероятностная модель явления определена с точностью до неизвестных параметров, которые и выясняются с помощью «пробных» испытаний. Математическая статистика активно применяется в экономике, в научных исследованиях, её рассматривают как науку о принятии решений в условиях неопределённости.

Одним из основных понятий теории вероятностей и математической статистики является понятие события.

Определение 1.Событие – результат (исход) некоторого испытания (опыта, эксперимента, наблюдения).

Например,

а) стрелок стреляет по мишени, разделённой на 4 области.

Выстрел – это испытание, попадание в определённую область мишени – это событие.

б) В урне имеются цветные шары. Из урны наудачу берут один шар.

Извлечение шара из урны - это испытание, появление шара определённого цвета - это событие.

События обозначаются большими латинскими буквами А, В, С,…

Предметом теории вероятностей является изучение вероятностных закономерностей массовых случайных событий, которые могут многократно наблюдаться при осуществлении одних и тех же условий.

Случайные события могут быть разных видов. Рассмотрим некоторые из них.

Определение 2.Несовместные события – случайные события, которые не могут появиться в одном испытании одновременно.

Например, брошена монета, появление «герба» исключает появление «надписи», события «появился герб» и «появилась надпись» - несовместные.

Определение 3.Полная группа событий – несколько случайных событий, для которых выполняется условие: в результате испытания происходит хотя бы одно из них, т.е. появление хотя бы одного из них в ходе испытания – достоверное событие.

Если имеется полная группа попарно несовместных событий, то в ходе испытания происходит только одно из них.

Например,

а) при составлении прогноза вида осадков на апрель – май полную группу событий составят события:

- « выпадет дождь»;

- « выпадет снег»;

- « выпадет град»;

- «отсутствие осадков»;

б) при двух выстрелах по мишени полную группу попарно несовместных событий составляют события: «два промаха», «два попадания», «один промах и одно попадание»;

в) при бросании игральной кости полную группу попарно несовместных событий составляют события:

- «выпало 1 очко»;

- «выпало 2 очка»;

- «выпало 3 очка»;

- «выпало 4 очка»;

- «выпало 5 очков»;

- «выпало 6 очков».

Определение 4.События называются равновероятными (равновозмож-

ными), если в появлении одного из них нет преимуществ перед другими.

Например, появление того или иного числа очков при подбрасывании кости – равновероятные события.

Центральным понятием теории вероятностей является понятие вероятности.

Определение 5.Вероятность – это число, характеризующее степень возможности появления события.

Условимся различать составные (разложимые) события и элементарные (неразложимые) события. Например, событие B – «при бросании двух игральных костей сумма выпавших очков равна 5» означает, что в результате испытания мог быть получен один из следующих исходов: (1.4) – на первой кости выпало 1 очко, а на второй – 4, а также аналогично имеют место исходы (2.3), (3.2), (4.1). То есть событие B разлагается на 4 элементарных события и является составным.

Заметим, что любое составное событие – это совокупность элементарных событий, каждое из которых соответствует одному и только одному неразложимому исходу испытания.

Рассмотрим классическое определение вероятности события, используя для его иллюстрации следующий пример.

Пример. В урне имеется 6 одинаковых тщательно перемешанных шаров, при этом 2 из них – красные, 3 – синие, 1 – белый. Дать количественную оценку того, что наудачу взятый шар – цветной.

Решение.

Пусть А – событие, состоящее в появлении цветного шара.

Каждый результат испытания (извлечение шара) – элементарное событие. Поскольку в урне 6 шаров, и в ходе испытания мы можем вытащить любой из них, то данному испытанию соответствуют 6 элементарных событий:

- «появился белый шар»;

- «появился красный шар»;

- «появился синий шар».

Эти события попарно несовместны, равновозможны и составляют полную группу.

Таким образом, событию А благоприятствуют следующие элементарные события : , , т.е. событие А наступит, если произойдёт либо , либо , либо , либо , либо .

Определение 6 (классическое определение вероятности).Отношение числа благоприятствующих событию А элементарных событий (исходов) к общему числу всех равновозможных попарно несовместных элементарных событий, образующих полную группу, называется вероятностью события А и обозначается , т.е.

, где

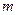- число благоприятствующих элементарных исходов испытания,

- общее число равновозможных попарно несовместных образующих полную группу элементарных исходов испытания.

В данном примере .

Свойства вероятности:

1. , если - достоверное событие;

2. , если - невозможное событие;

3. , если - случайное событие;

4. , где - элементарное событие ( , благоприятствующее событию .

Следствие: , если - произвольное событие.

Таким образом, вероятность события – это число, принадлежащее отрезку .

Примеры.

1) В урне 12 шаров: 3 белых, 4 чёрных и 5 красных. Какова вероятность вынуть из урны чёрный шар?

Решение.

Обозначим через - событие, состоящее в том, что из урны вынули чёрный шар.

Поскольку необходимо найти вероятность появления чёрного шара, а всего чёрных шаров 4, то - число благоприятствующих элементарных исходов испытания.

Поскольку в урне 12 шаров и можно вынуть любой из них, то - общее число всех исходов испытания. Воспользуемся классическим определением вероятности события, тогда .

Ответ: .

2) В колоде 36 карт. Наудачу вынимают из колоды 2 карты. Определите вероятность того, что вторым вынут туз, если первым тоже вынут туз.

Решение.

Пусть - событие, состоящее в том, что вторым из колоды вынут туз, если первым был вынут туз.

Всего в колоде 36 карт. Поскольку из неё вынут один туз, то в ней осталось 3 туза, каждый из которых может быть вынут в ходе испытания, поэтому - число благоприятствующих событию исходов испытания.

Так как из колоды уже вынули одну карту, то в ней осталось 35 карт, каждая из которых может быть вынута в ходе испытания, тогда - общее число всех элементарных исходов испытания.

Значит,

Ответ: .

Определение 7.Суммой событий А и В называется событие, состоящее в появлении хотя бы одного из этих событий, т.е. или события А, или события В, или обоих событий А и В.

Теорема 1.Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий, т.е.

Пример. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1 , 9 очков – 0,3 , 8 или меньше очков – 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

Решение.

Заметим, что слова «не менее 9» означают 9 или более, в данном случае - 9 или 10.

Пусть - событие, состоящее в том, что при одном выстреле стрелок выбьет не менее 9 очков;

- событие, состоящее в том, что стрелок при одном выстреле выбьет 10 очков;

- событие, состоящее в том, стрелок при одном выстреле выбьет 9 очков.

Тогда , где и - несовместные. Значит, .

Ответ:0,4.

Определение 8.Произведением событий А и В называется событие, состоящее в одновременном появлении этих событий.

Определение 9.Если вероятность события не зависит от того, происходит ли оно до события , или после него, то и называются независимыми событиями. В противном случае, и - зависимые события.

Например, «появление герба на белой монете при одном подбрасывании монеты» и «появление герба на жёлтой монете при одном подбрасывании монеты» – независимые события, а события «появление герба при одном подбрасывании монеты» и «появление надписи при одном подбрасывании монеты» - зависимые, т.к. появление одного из них обращает в нуль вероятность появления другого.

Теорема 2.Вероятность произведения независимых событий равна произведению вероятностей этих событий, т.е. , если и - независимые события.

Пример. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из двух проверенных изделий оба стандартные.

Решение.

Введём в рассмотрение события , , 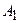, означающие следующее:

- «оба изделия стандартные»,

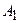- «первое изделие – стандартное», - «второе изделие – стандартное». Тогда событие можно записать в виде: .

Так как события 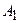и - независимые, то найдём вероятность события , руководствуясь теоремой 2:

Ответ:0,64.

Определение 10.Вероятность события А, вычисленная при условии, что до него имело место событие В, называется условной вероятностью события и обозначается или .

Теорема 3.Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило, т.е. .

Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причём вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились, т.е.

.

Пример. В лотерее 1000 билетов. Из них 500 – выигрышные, 500 – невыигрышные. Куплено 2 билета. Какова вероятность, что оба билета выигрышные?

Решение.

Пусть - событие «оба билета – выигрышные», - событие «первый билет - выигрышный», - событие «второй билет – выигрышный».

Тогда , причём и - зависимые события, т.к. вероятность события зависит от того, произошло до него событие или нет (если произошло, то вероятность события будет меньше, нежели в случае, если не произошло).

Значит, .

. Отсюда .

Ответ: .

Во многих задачах на классическую вероятность часто для подсчёта этой вероятности используют формулы комбинаторики, которые позволяют ускорить процесс подсчёта чисел 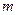и .

Элементы комбинаторики

Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных элементов. При этом под комбинациями понимаются группы элементов, отличающиеся одна от другой или порядком следования элементов, или самими этими элементами.

Комбинаторные задачи бывают самых разных видов, но большинство из них решается с помощью двух основных правил: правила произведения и правила суммы.

Правило произведения. Если объект 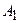может быть выбран 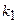способами из имеющихся элементов, объект 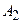- 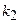способами из оставшихся элементов, объект 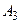- 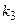способами и т.д., то существует 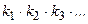способов выбора совокупности объектов .

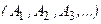Пример. В группе 25 студентов. Сколькими способами можно выбрать в этой группе старосту, профорга и физорга?

Решение.

1. Старостой может быть каждый студент, тогда имеется 25 возможностей выбора старосты.

2. После выбора старосты осталось 24 студента, любой из них может быть профоргом. Следовательно, имеется 24 возможности выбора профорга.

3. Аналогично рассуждая, получаем 23 возможности выбора физорга.

Выбор старосты сочетается с выбором профорга и с выбором физорга.

Таким образом, всего возможностей выбора трёх должностей будет .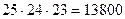

Ответ: 13800.

Правило суммы. Если множество 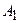состоит из 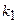элементов, 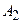- из 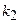элементов, …, причём эти множества не имеют общих элементов, то выбор элемента либо из 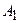, либо из 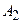, … можно осуществить 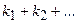способами.

Пример. На книжной полке стоит 20 книг по алгебре, 12 – по теории вероятностей, 7 – по истории, 25 – по литературе и 6 – по геометрии. Сколькими способами можно выбрать книгу по математике?

Решение.

Всего книг по математике 20+12+6=38. Значит, имеется 38 способов выбора книги по математике.

Ответ:38.

Существуют три вида комбинаций, среди элементов которых нет повторяющихся, это: перестановки, размещения, сочетания.

Определение 11.Перестановки из элементов – комбинации, состоящие из всех элементов и отличающиеся друг от друга лишь порядком следования элементов.

Обозначаются перестановки из элементов - 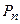, при этом вычисляется число таких комбинаций по формуле

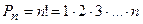
Полагаем, что 0!=1!=1.

Примеры.

1) Сколько пятизначных чисел можно составить из цифр 0,2,4,6,8, если числа в цифрах не повторяются.

Решение.

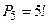- число способов перестановки пяти цифр.

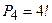- число «пятизначных» чисел, начинающихся с «0». Тогда 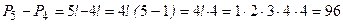- число пятизначных чисел.

Ответ:96.

2) На трёх карточках написаны буквы У, К, Ж. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность, что получится слово «ЖУК»?

Решение.

Пусть - событие «получится слово «ЖУК».

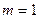- число способов получения слова «ЖУК» из букв У, К, Ж;

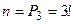- число слов, которые можно получить из букв У, К, Ж.

Значит, .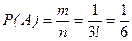

Ответ: .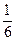

3) На один ряд из 7 мест случайным образом рассаживаются 7 учеников. Найдите вероятность того, что 3 определённых ученика окажутся рядом.

Решение.

Пусть - событие, состоящее в том, что из 7 человек 3 определённых окажутся рядом. Найдём вероятность события , используя классическое определение вероятности.

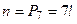- общее число способов рассаживания 7 учеников,

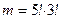- число способов рассаживания 7 учеников, когда 3 определённых ученика окажутся рядом (3 ученика рассматриваются как один, тогда 1+4=5 учеников можно рассадить 5! способами, при этом внутри «тройки» ученики могут пересаживаться 3! способами; так как одни способы рассаживания нужно рассматривать в совокупности с другими, то по правилу произведения получим 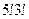способов рассаживания учеников).

Значит, .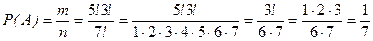

Ответ: .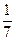

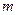Определение 12.Размещения из элементов по - комбинации, каждая из которых содержит 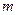элементов из данных , при этом одна комбинация отличается от другой либо составом элементов, либо порядком расположения элементов.

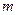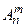Обозначение размещений из элементов по - . Вычисляется число таких комбинаций по формуле

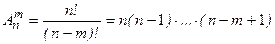, где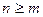

Примеры.

1) Сколько различных натуральных чисел можно записать с помощью цифр 0, 1, 2, 3, 4, если цифры в числах не повторяются?

Решение.

Поскольку числа – упорядоченные наборы цифр, отличающиеся один от другого либо порядком следования цифр, либо составом цифр, тогда для подсчёта количества однозначных, двузначных и других чисел нужно применять размещения.

Подсчитаем количество однозначных, двузначных, трёхзначных, четырёхзначных и пятизначных чисел, которые можно составить из данных цифр.

Количество однозначных чисел - 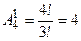(это числа 1, 2, 3, 4).

Количество двузначных чисел - 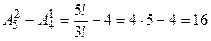(так как 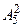- число упорядоченных пар цифр, составленных из 0,1,2,3,4, то среди них могут быть числа вида 01, 02, 03, 04, которые не являются двузначными; количество таких чисел равно числу размещений ).

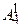Количество трёхзначных чисел - 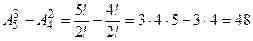( 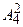- число «трёхзначных» чисел, начинающихся с «0»).

Количество четырехзначных чисел - .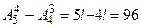

Количество пятизначных чисел - .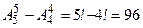

Итак, общее число натуральных чисел, записанных с помощью цифр 0,1, 2, 3, 4, равно: 4+16+48+96+96=260.

Ответ:260.

2) Из букв слова «событие», составленного с помощью разрезной азбуки, извлекаются наудачу и складываются друг за другом в порядке их извлечения 3 карточки (буквы). Какова вероятность получить при этом слово «быт»?

Решение.

Пусть - событие, состоящее в том, что получено слово «быт».

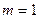- число способов получения слова «быт» (это слово получится только при условии: если из трёх извлечённых карточек первой будет буква «б», второй – «ы», третьей – «т»).

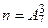- общее число способов извлечения трёх карточек из семи.

Тогда .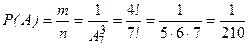

Ответ: .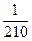

3) Числа 1,2,3,4,5 написаны на 5 карточках. Наудачу последовательно вынимаются 3 карточки, и вынутые таким образом цифры ставятся слева направо. Чему равна вероятность того, что полученное таким образом трёхзначное число окажется чётным?

Решение.

Виды трёхзначных чётных чисел, составленных из указанных цифр: 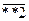и .

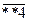- событие «получено чётное трёхзначное число».

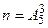- общее число полученных трёхзначных чисел;

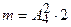- число чётных трёхзначных чисел указанного выше вида, где 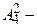число способов заполнения ** в одной модели чётного числа (т.к. одна цифра уже задействована, то две цифры из четырёх с учётом порядка можно взять числом способов, равным ).

.

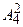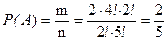Ответ: .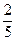

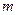Определение 13.Сочетания из элементов по - комбинации, каждая из которых содержит 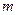элементов из данных , при этом одна комбинация отличается от другой лишь составом элементов, но не порядком расположения элементов.

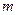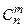Обозначение сочетаний из элементов по - . Вычисляется число таких комбинаций по формуле , где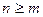

Примеры.

1) Сколькими различными способами можно назначить в патруль трёх солдат и одного офицера, если имеется 15 солдат и 4 офицера?

Решение.

Трёх солдат из 15 можно выбрать: способами (порядок следования солдат в каждой выборке неважен).

Одного офицера из четырёх можно выбрать: способами.

Выбор офицера сочетается с выбором солдата, поэтому всего способов: .

Ответ: 1820 способов.

2) В экзаменационный билет входят 4 вопроса программы, насчитывающей 45 вопросов. Абитуриент не знает 15 вопросов программы. Какова вероятность того, что он вытянет билет, где все вопросы ему известны?

Решение.

1 способ.

Пусть - событие, состоящее в том, что студент вытянет билет, где все вопросы ему известны.

- общее число способов формирования билетов для экзамена;

- число удачных для студента способов формирования билетов.

.

2 способ.

Данную задачу можно решить иначе, если рассмотреть как событие, состоящее в одновременном появлении следующих событий:

- «студент знает 1-ый вопрос билета»,

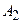- «студент знает 2-ой вопрос билета»,

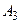- «студент знает 3-ий вопрос билета»,

- «студент знает 4-ый вопрос билета».

Таким образом, , где , , 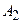, 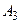- зависимые события. Тогда Ответ: 0,2.

3) В коробке 4 красных и 6 зелёных карандашей. Случайно выпало 3 карандаша. Какова вероятность того, что 2 из них – красные?

Решение.

Пусть - событие, состоящее в том, что из трёх выпавших карандашей 2 – красные.

- число способов выбора 3 карандашей из 10;

- число способов выбора 2 красных и 3-2=1 зелёного карандаша (каждый способ выбора 2-ух красных карандашей нужно рассматривать в совокупности с каждым способом выбора 1 зелёного карандаша).

.

Ответ: 0,3.

Задания для самоконтроля

1) Бросается один раз игральная кость. Определите вероятность выпадения 3 или 5 очков.

2) В урне 3 белых и 3 чёрных шара. Из неё дважды вынимают по одному шару, не возвращая их обратно. Найдите вероятность появления белого шара при втором испытании, если при первом испытании был извлечён чёрный шар.

3) Монета подброшена 2 раза. Какова вероятность того, что оба раза выпадет «герб».

4) 8 различных книг расставлены наудачу на одной полке. Найти вероятность того, что две определённые книги окажутся поставленными рядом.

5) Имеется 12 лотерейных билетов. Из них 7 – выигрышные. Наудачу берут 6 билетов. Какова вероятность того, что 4 из них – выигрышные?

6) На карточках написаны целые числа от 1 до 15 включительно. Наудачу извлекаются 2 карточки. Какова вероятность того, что сумма чисел, написанных на этих карточках, равна 10?

7) Имеются цифры 1,2,3,4,5,6,7, написанные на карточках, которые тщательно перемешиваются. Человек наудачу называет трёхзначное число с разными цифрами, начинающееся с «2», а затем произвольно вынимает три карточки и раскладывает их в порядке следования. Какова вероятность того, что он получит названное им число?

Ответы: 1) ; 2) 0,6; 3) ; 4) ; 5) ; 6) ; 7) .

Формула полной вероятности

Пусть имеется урн с разным количеством белых и чёрных шаров. Кто-то наудачу выбирает урну, а затем уже из неё наудачу один шар. Какова вероятность того, что выбранный шар окажется белым?

Событие - выбранному шару оказаться белым происходит совместно с событием «выбор урны».

Событие - искомое,события («выбор -ой урны, где ) – события-гипотезы. Они попарно несовместны. Для поиска вероятности события руководствуются следующей теоремой.

Теорема.Вероятность события , которое может наступить лишь при условии появления одного из попарно несовместных событий -гипотез , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий-гипотез на соответствующую условную вероятность события , т.е.

(*)

Формула (*) называется формулой полной вероятности события .

Рассмотрим примеры применения данной теоремы.

1) Имеются три одинаковые урны. В первой находятся 4 белых и 6 чёрных шаров, во второй – 7 белых и 3 чёрных и в третьей – только чёрные. Наудачу выбирается урна и из неё наугад вынимается один шар. Какова вероятность того, что будет выбран: а)чёрный; б) белый шар?

Решение.

а) Пусть - событие «из урны вынули чёрный шар».

- гипотеза «выбрали первую урну»;

- гипотеза «выбрали вторую урну»;

- гипотеза «выбрали третью урну».

Поскольку , , - равновероятные и образуют полную группу, то .

Тогда - вероятность того, что из первой урны достанут чёрный шар.

- вероятность того, что из второй урны достанут чёрный шар. - вероятность того, что из третьей урны достанут чёрный шар.

Значит, .

- вероятность того, что из наудачу выбранной урны наудачу возьмут чёрный шар.

б) Пусть - событие «из урны вынули белый шар».

- гипотеза «выбрали первую урну»;

- гипотеза «выбрали вторую урну»;

- гипотеза «выбрали третью урну».

.

Тогда - вероятность того, что из первой урны наудачу достанут белый шар.

- вероятность того, что из второй урны наудачу достанут белый шар. - вероятность того, что из третьей урны наудачу достанут белый шар.

Значит, , т.е.

- вероятность того, что из наудачу выбранной урны наудачу возьмут белый шар.

Ответ: а) б) .

2) В первом ящике 20 деталей, из них 15 стандартных, во втором – 30 деталей, из них 24 стандартных, в третьем - 10 деталей, из них 6 стандартных. Содержимое ящиков разместили в шкафу. Найти вероятность того, что наудачу извлечённая из шкафа деталь– стандартная.

Решение.

Пусть - событие «наудачу извлечённая из шкафа деталь – стандартная».

- гипотеза «деталь принадлежит первому ящику»;

- гипотеза «деталь принадлежит второму ящику»;

- гипотеза «деталь принадлежит третьему ящику».

Ящики содержат разное количество деталей, поэтому события , , - не равновероятные.

Общее количество деталей в трёх ящиках – 20+30+10=60. Тогда - вероятность того, что извлечённая деталь принадлежит первому ящику.

Аналогично, , .

Найдём условные вероятности события