Причины возникновения корреляционной зависимости

1.Наличие причинно-следственной связи между изучаемыми явлениями или признаками.

2.Наличие общего фактора, вызывающего имение корреляционно связанных признаков (ложная корреляция).

Когда вариация двух признаков говорит о наличии между ними корреляционной зависимости при фактическом отсутствии связи, а соответствующая вариация вызвана наличием общего фактора.

3.Наличие взаимосвязи между признаками. Один и тот же признак может выступать то фактором, то результатом.

При изучении корреляционной зависимости важно теоретически обосновать наличие корреляции и причинно-следственной зависимости, так как полученные высокие показатели корреляции не являются свидетельством причинно-следственной зависимости. Если она не обоснована, то можно столкнуться с так называемой ложной корреляцией.

Существуют понятия парной корреляционной зависимости и множественной корреляционной зависимости.

Парная корреляционная зависимость – зависимость между двумя признаками, один из которых – признак-результат или зависимая переменная, второй – признак-фактор или независимая переменная.

Множественная корреляционная зависимость – зависимость между одним признаком-результатом и двумя и более признаками-факторами.

Учитывая сложность социально-экономических явлений, стоит предположить, что парных связей в принципе не существует.

Изучение влияния одного фактора на признак-результат связано с практической потребностью оценить степень влияния именно данного конкретного фактора. Среди множества факторов выделяют один, занимающий лидирующее место среди множества факторов, определенно оказывающих влияние на анализируемый признак-результат.

Показатели корреляции называются показателями или характеристиками тесноты корреляционной связи. К этим показателям относятся:

Ø Коэффициент корреляции (парный, множественный и частный).

Ø Коэффициент детерминации (парный, множественный и частный).

Ø Корреляционное отношение (эмпирическое и теоретическое).

Ø Индекс корреляции.

Коэффициент корреляции

Исторически первым показателем тесноты связи был парный коэффициент корреляции, предложенный Пирсоном. Он основан на сопоставлении вариации признака-фактора и признака-результата.

cov =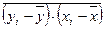

Среднее значение произведения отклонений индивидуальных значений результативного признака от своего среднего называется ковариацией (показатель оценивает совместное изменение двух признаков).

Однако показатель ковариации сложно содержательно комментировать. Нормированное значение показателя ковариации – это парный показатель корреляции Пирсона.

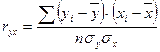
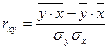
Достоинства коэффициента корреляции: величина изменяется по модулю от нуля до единицы. Близость коэффициента к нулю свидетельствует об отсутствии корреляционной зависимости. Близость к единице – о тесной корреляционной зависимости.

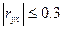- связь практически отсутствует;

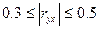- связь заметная;

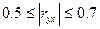- связь умеренная;

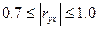- связь заметная.

Парный коэффициент корреляции – симметричный показатель: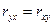

Это означает, что высокое значение коэффициента корреляции не подтверждает причинно-следственной связи. Что есть фактор, а что есть результат, не имеет значения. Эта связь устанавливается на основе теоретического анализа изучаемого объекта.

Знак при коэффициенте корреляции означает наличие прямой или обратной зависимости.

Коэффициент детерминации

Необходимость оценки парной зависимости связана с темя, что из множества факторов, определяющих результат, очень часто выделяются доминирующие факторы, то есть оказывающие наибольшее влияние. Иногда целью исследования является изучение влияния одного конкретного фактора.

Чаще на практике изучается множественная корреляционная зависимость, когда изучается влияние двух и более факторов на признак-результат. Теснота связи между комплексом факторов и результативным признаком оценивается с помощью множественного коэффициента корреляции.

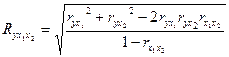
r² – показатель, который называется коэффициентом детерминации. Он характеризует долю объясненной дисперсии результативного признака, то есть долю факторной дисперсии в общей дисперсии результативного признака.

Множественный коэффициент корреляции изменяется от нуля до единицы. Комментарий конкретных значений множественного коэффициента корреляции аналогичен комментарию значений парногокоэффициента корреляции.

Квадрат множественного коэффициента корреляции R² – множественный коэффициент детерминации, который характеризует долю факторной дисперсии результативного признака в общей дисперсии, выражается, как правило, в процентах.

Факторная дисперсия – это дисперсия признака-результата, обусловленная вариацией признаков-факторов, включенных в анализ.

Остаточная дисперсия – это дисперсия признака-результата, обусловленная влиянием факторов, не включенных в анализ.

Общая дисперсияпризнака-результата обусловлена всеми факторами, влияющими на результат.

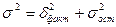
Пример:

R²=0.67=67% . Вариация показателя рождаемости в регионах Российской Федерации на 67% обусловлена показателем среднедушевого дохода.

При изучении множественной корреляционной зависимости рассчитывается также частный коэффициент корреляции, характеризующий тесноту связи между одним признаком фактором и признаком-результатом при условии элиминирования влияния других факторов, включенных в анализ.

При элиминировании (абстрагирование от остальных факторов) значение факторов закрепляется, как правило, на среднем уровне, кроме того фактора, для которого рассчитывается коэффициент корреляции.

При двухфакторной корреляционной зависимости рассчитывается два частных коэффициента корреляции.

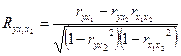
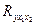- данный коэффициент характеризует слепень тесноты корреляционной зависимости между результатом (y) и фактором (x₁) при элиминировании фактора x_2.

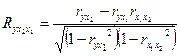
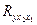- данный коэффициент характеризует тесноту зависимости признака-результата (y) от признака- фактора (x₂) при элиминировании фактора x_1.

Квадрат частного коэффициента корреляции ( 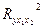) - это частный коэффициент детерминации

Корреляционное отношение

Коэффициенты корреляции пригодны в большей для оценки линейной зависимости между изучаемыми признаками. Если связь нелинейная, то следует отдать предпочтение показателю, который называется корреляционное отношение. Оно может быть:

Ø Эмпирическое (т.е. рассчитанное по данным аналитической группировки).

Ø Теоретическое (т.е. рассчитанное по результатам регрессионного анализа).

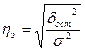- эмпирическое

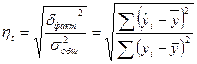- теоретическое

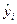- выровненное или полученное по уравнению регрессии значение признака-результата у i-ой единицы теоретическое значение признака-результата.

y_i – исходные данные.

Корреляционное отношение изменяется также от нуля до единицы и комментируется аналогично коэффициенту корреляции.

Квадрат корреляционного отношения ( 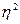)- коэффициент детерминации.

Индекс корреляции

Индекс корреляции рассчитывается по следующей формуле:

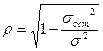
28. Множественный и частный коэффициенты корреляции.

Необходимость оценки парной зависимости связана с темя, что из множества факторов, определяющих результат, очень часто выделяются доминирующие факторы, то есть оказывающие наибольшее влияние. Иногда целью исследования является изучение влияния одного конкретного фактора.

Чаще на практике изучается множественная корреляционная зависимость, когда изучается влияние двух и более факторов на признак-результат. Теснота связи между комплексом факторов и результативным признаком оценивается с помощью множественного коэффициента корреляции.

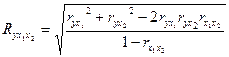
r² – показатель, который называется коэффициентом детерминации. Он характеризует долю объясненной дисперсии результативного признака, то есть долю факторной дисперсии в общей дисперсии результативного признака.

Множественный коэффициент корреляции изменяется от нуля до единицы. Комментарий конкретных значений множественного коэффициента корреляции аналогичен комментарию значений парногокоэффициента корреляции.

Квадрат множественного коэффициента корреляции R² – множественный коэффициент детерминации, который характеризует долю факторной дисперсии результативного признака в общей дисперсии, выражается, как правило, в процентах.

При изучении множественной корреляционной зависимости рассчитывается также частный коэффициент корреляции, характеризующий тесноту связи между одним признаком фактором и признаком-результатом при условии элиминирования влияния других факторов, включенных в анализ.

При элиминировании (абстрагирование от остальных факторов) значение факторов закрепляется, как правило, на среднем уровне, кроме того фактора, для которого рассчитывается коэффициент корреляции.

При двухфакторной корреляционной зависимости рассчитывается два частных коэффициента корреляции.

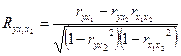
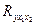- данный коэффициент характеризует слепень тесноты корреляционной зависимости между результатом (y) и фактором (x₁) при элиминировании фактора x_2.

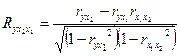
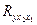- данный коэффициент характеризует тесноту зависимости признака-результата (y) от признака- фактора (x₂) при элиминировании фактора x_1.

Квадрат частного коэффициента корреляции ( 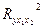) - это частный коэффициент детерминации.

29. Парная линейная регрессия. Коэффициенте регрессии.

Простейшим видом уравнения регрессии является парная линейная зависимость.

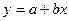
где y – зависимая переменная (признак-результат),

x – независимая переменная (признак-фактор).

В качестве уравнения регрессии могут быть выбраны различные математические функции: чаще всего исследуется линейная зависимость, парабола, гипербола, степная функция. Но исследование начинается с линейной зависимости, так как результаты поддаются содержательной интерпретации.

При нанесении на поле корреляции точек, координаты которых соответствуют значениям зависимых и независимых переменных выявляется тенденция связи между ними.

Смысл построения уравнения регрессии состоит в описании тенденции зависимости признака-результата от признака-фактора.

Если линия регрессии проходит через все точки поля корреляции, то эта функциональная связь. Так как всегда присутствует ошибка, поэтому нет функциональной связи.

Наличие ошибки связано с тем что:

§ не все факторы, влияющие на результат, учитываются в уравнении регрессии;

§ может быть неправильно выбрано уравнение регрессии или форма связи.

Уравнение регрессии описывает изменения условного среднего значения признака-результата под влиянием конкретных значений признака-фактора, то есть это аналитическая форма тенденции зависимости между изучаемыми признаками. Уравнение регрессии строится на основе фактических значений признаков, и для его использования нужно рассчитать параметры уравнения а и b. Определение значений параметров, как правило, выполняется с использованием методов наименьших квадратов (МНК).

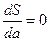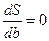Проводя дифференцирование, приравниваем частные производные к нулю и , получаем систему уравнений. Решая ее, находим значения параметров а и в.

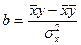
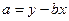
Параметр в в уравнении регрессии называется коэффициентом регрессии и характеризует на сколько единиц своего измерения изменится признак-результат при изменении признака-фактора на единицу своего измерения. Знак при коэффициенте регрессии характеризует направленность зависимости (прямая или обратная). Параметр а в уравнении регрессии содержательно не интерпретируется, а характеризует лишь расположение линии на графике.

Пример.

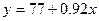
Данное уравнение показывает тенденцию зависимости заработной платы (у) от прожиточного минимума (х). Коэффициент в (в данном случае равный 0,92) характеризует следующее: при увеличении на 1 рубль потребительской корзины заработная плата возрастает на 92 копейки.

30. Расчет параметров уравнения регрессии. Метод наименьших квадратов.

Уравнение регрессии описывает изменения условного среднего значения признака-результата под влиянием конкретных значений признака-фактора, то есть это аналитическая форма тенденции зависимости между изучаемыми признаками. Уравнение регрессии строится на основе фактических значений признаков, и для его использования нужно рассчитать параметры уравнения а и b. Определение значений параметров, как правило, выполняется с использованием методов наименьших квадратов (МНК).

Суть метода состоит в том, что удается минимизировать сумму квадратов отклонений фактических значений признака-результата от теоретических, рассчитанных на основе уравнения регрессии, что оценивает степень аппроксимации поля корреляции уравнением регрессии.

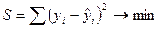
Задача состоит в решении задачи на экстремум, то есть найти при каких значениях параметров а и в функции S достигает минимума.

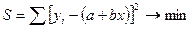
Проводя дифференцирование, приравниваем частные производные к нулю 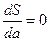и 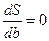, получаем систему уравнений. Решая ее, находим значения параметров а и в.

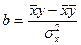
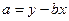
Параметр в в уравнении регрессии называется коэффициентом регрессии и характеризует на сколько единиц своего измерения изменится признак-результат при изменении признака-фактора на единицу своего измерения. Знак при коэффициенте регрессии характеризует направленность зависимости (прямая или обратная). Параметр а в уравнении регрессии содержательно не интерпретируется, а характеризует лишь расположение линии на графике.

31. Множественная регрессия. Проверка статистической значимости параметров уравнения и уравнения в целом

Уравнение множественной регрессии – аналитическая форма зависимости признака-результата от двух или более признаков-факторов.

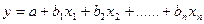
в - коэффициент регрессии

В уравнении множественной регрессии их называют условно чистыми коэффициентами. Их можно назвать чистыми коэффициентами, если бы в уравнении регрессии удалось включить все факторы определяющие результат..

Это невозможно пор нескольким причинам:

§ Ограниченный объем совокупности (число факторов должно 5-6 раз, идеально в 10 раз, меньше объема совокупности).

§ Не по всем факторам имеются данные.

§ Не все факторы имеют количественную оценку.

§ Не знаем о факторах, которые реально влияют на результат.

Интерпретация коэффициентов множественной регрессии аналогична интерпретации коэффициентов парной регрессии.

Коэффициент регрессии во множественном уравнении регрессии не равен коэффициенту регрессии в парном уравнении регрессии (при оценке влияния одного итого же фактора), так как в уравнении множественной регрессии величина коэффициента рассчитывается в условиях элиминирования влияния ряда факторов, включенных в уравнение.