Этапы статистического исследования

Этапы статистического исследования

I Статистическое наблюдение.

II Сводка и группировка исходных данных.

III Анализ информации, оценка статистических гипотез.

Статистическое наблюдение

Статистическое наблюдение – научно обоснованный сбор массовой информации, заключающийся в регистрации значений признаков у каждой единицы совокупности. В результате наблюдения может быть получен одномерный массив данных, когда по каждой единице совокупности фиксируется значение только одного признака. На основе таких данных возможно:

- оценить типический уровень изучаемого признака;

- изучить структуру совокупности, то есть структуру распределения единиц по данному признаку;

- изучить степень вариации изучаемого признака относительно типического уровня;

- подобрать теоретическое распределение, описывающее изучаемое фактическое.

Двумерный массив данных.

К перечисленным возможностям анализа добавляется возможность оценки наличия или отсутствия связи и зависимости между изучаемыми признаками, и построение соответствующих моделей.

Многомерный массив данных.

Его наличие позволяет кроме отмеченных в предыдущих пунктах направлений анализа, оценить совокупное влияние нескольких факторов на интересующий исследователя признак, а также ранжировать факторы по степени их влияния.

Статистическое наблюдение по степени охвата единиц совокупности может быть:

- сплошное (признаки фиксируются у всех единиц изучаемой совокупности);

- несплошное (признаки фиксируются у части единиц совокупности).

В настоящее время сплошное статистическое наблюдение встречается редко. Пример: единый государственный регистр предприятий и организаций.

Несплошное:

1) выборочное

Из генеральной совокупности случайным образом формируется так называемая выборочная совокупность, и значение признаков регистрируется только у единиц, попавших в выборку. По результатам анализа в выборочной совокупности с определенной вероятностью дается оценка генеральной совокупности. Самое распространенное наблюдение.

2) наблюдение основного массива

Признаки фиксируются у единиц совокупности, которые влияют на формирование основного результата функционирования данной совокупности.

3) монографическое

Углубленное изучение отдельных единиц совокупности, например, предприятий с прогрессивными формами организации труда или внедряющих новые технологии.

По времени наблюдения статистическое наблюдение может быть:

1) текущим (непрерывным). Регистрация фактов осуществляется по мере их возникновения. Пример: запись в Загсе, регистрация внутри фирмы.

2) периодическим. Повторяется с определенным интервалом. Пример: перепись населения.

3) единовременным. Наблюдения, которые могут повторятся и которые не могут. Как правило ориентированы на текущие потребности и запросы различных управленческих структур.

По форме наблюдения статистическое наблюдение может быть:

1) непосредственное наблюдение. Связано со сбором первичных данных.

2) документальное. Сбор вторичных данных.

3) опрос. Корреспондентский опрос, саморегистрация и экспедиционный способ опроса.

Требования к статистическому наблюдению:

- полнота охвата фактов;

- достоверность и сопоставимость;

- объективность.

Для выполнения этих требований на стадии подготовки наблюдения должен быть решен широкий круг вопросов:

1. Четко сформулированы цель и задачи наблюдения.
2. Определен объект наблюдения, то есть должны быть названы основные признаки, по которым единицы будут включаться в статистическую совокупность.
3. Определено время проведения наблюдения, а при регистрации непрерывно меняющихся признаков определен фактический момент наблюдения.
4. Должны быть выбраны методы сбора, обработки и анализа информации.
5. Должна быть выбрана форма представления результатов.
6. Разработана программа наблюдения.

Программа наблюдения – перечень признаков, значение которых будет регистрироваться, или перечень вопросов, на которые предстоит получить ответ.

Все перечисленные пункты – это методологические вопросы наблюдения.

На стадии подготовки наблюдения также решаются организационные вопросы: подготовка кадров, разработка и подготовка формуляров наблюдения (бланки счетов…).

5. Сводка и группировка как этапы статистического исследования.

Статистические данные, собранные в результате наблюдения, в своем первоначальном виде труднообозримы и без предварительной их подготовки не пригодны для проведения углубленного анализа.

Большую роль в разработке статистических данных играют современные классификаторы технико-экономической и социальной информации. Начиная с 2003 года по постановлению правительства России Госкомстат (с 2004г – Росстат) ведет большую работу по разработке классификаторов и их гармонизации с международными аналогами.

Классификаторы – это важнейший инструмент систематизации, упорядочения и сопоставимости данных. Их использование позволяет получить стандартные группировки в статистических отчетах, статистических формах, в средствах электронной обработки, а также в выходных статистических материалах и публикациях.

В России в настоящее время разработаны классификаторы, которые позволяют по единой методике сгруппировать информацию и охарактеризовать структуру национальной экономики, природных и трудовых ресурсов, административно-территориальное деление страны, виды производимых товаров и услуг и ряда других экономических и социальных объектов и их свойств.

Сводка как процедура сжатия, уплотнения и упорядочения информации является обязательным этапом исследования любого уровня. Основной прием сводки – группировка.

Группировка – разбиение или разделение статистической совокупности на отдельные группы по одному или нескольким признакам.

Признак, положенный в основу группировки – группировочный признак.

Если группировка единиц совокупности проводится по одному признаку, она называется простой или монотетической, если по двум или нескольким признакам – комбинационной.

Исходя из сложности социально-экономических явлений, предпочтения следовало бы отдать комбинационным группировкам. Однако чем больше используется группировочных признаков, тем менее обозрима и информативна получаемая группировка. Чрезмерная детализация информации может также привести к пустым или малонаполненным группам.

Использование группировок решает следующие основные задачи:

- выделение и описание объективно существующих типов и групп;

- изучение структуры совокупности и оценка структурных сдвигов;

- изучение связей и зависимостей между признаками.

6. Виды группировок, применяемых в статистике.

Использование группировок решает следующие основные задачи:

- выделение и описание объективно существующих типов и групп;

- изучение структуры совокупности и оценка структурных сдвигов;

- изучение связей и зависимостей между признаками.

Первая задача решается с помощью типологической группировки.

Группировочный признак – форма собственности. Результаты группировки – число занятых. Результат группировки представлен абсолютным показателем.

Вторая задача решается с использование структурной группировки. Структурная группировка, как привило, строится на базе типологической, но с использованием относительных показателей. То есть рассчитывается доля каждой группы в общем объеме совокупности.

При наличии структурной группировки за ряд лет может быть изучена динамика структуры, то есть структурные сдвиги.

Третья задача решается с использованием аналитической группировки. Аналитическая группировка строится на основе факторного признака, то есть признака, под влиянием которого изменяется другой признак, называемый результативным или результатом. По группам, сформированным на основе признака-фактора, рассчитывается средняя величина признака-результата. Изучение параллельных изменений этих признаков позволяет выдвигать гипотезу о наличии или отсутствии связи между признаками. Факторный признак – возраст. Признак-результат – хроническое заболевание.

Построение группировок предполагает решения следующих задач:

1. выбор группировочного признака. Выбор зависит от конкретных целей и задач исследования.

2. определение числа групп. На число групп оказывает влияние объем совокупности и тип группировочного признака. Если признак атрибутивный, то число групп соответствует числу объективно существующих типов в изучаемой совокупности (см Таблицу1). Если в качестве группировочного признака используется количественный дискретный признак, то число групп соответствует числу градаций этого признака. Основная проблема с определением числа групп связана с количественными непрерывными признаками. В этом случае число групп определяют по формуле Стерджесса:

K = 1 + 3.322 lgN , где

K- число выделяемых групп,

N – объем статистической совокупности.

Эта формула дает хорошие результаты при условии больших совокупностей, при N>100.

Определение числа групп обеспечивается интуицией, профессиональным опытом или результатами предыдущих аналогичных исследований.

3. После определения числа групп рассчитывают группировочный интервал

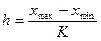, где

h – группировочный интервал,

K – число групп,

x_max, x_min – максимальное и минимальное значение признака совокупности.

Интервал группировки, помимо равного, может быть:

- прогрессивно возрастающим;

- прогрессивно убывающим;

- специализированным.

Это зависит от характера группировочного признака, степени вариации, целей исследования.

7. Виды статистических показателей,

Сложность социально-экономических явлений порождает необходимость их описания с использованием системы взаимосвязанных и взаимодополняющих показателей.

Показатели:

1) абсолютные. Показатели, характеризующие объем совокупности в целом, а также отдельных ее типов и групп или характеризующие объем признака как в целом по совокупности, так и в разрезе отдельных типов. Абсолютные показатели – это всегда именованные величины. Являясь основой расчета относительных и средних показателей, несут также определенную аналитическую нагрузку.

2) относительные. Рассчитываются как отношение тех или иных абсолютных характеристик или ранее рассчитанных относительных средних величин.

При сопоставлении одноименных абсолютных показателей получают следующие относительные показатели:

1. относительный показатель динамики (сопоставляя одноименные характеристики во времени);

2. относительный показатель структуры (отношение части к целому);

3. относительный показатель планового задания и выполнения плана;

4. относительный показатель координации (соотношение двух частей одного целого);

5. относительный показатель наглядности (сопоставление одноименных характеристик, относящихся к разным совокупностям).

В результате перечисленных сопоставлений получают коэффициенты или показатели, выраженные в процентах. При сопоставлении разноименных абсолютных величин получают относительные показатели интенсивности, характеризующие интенсивность распределения того или иного явления в определенной среде. К этим показателям относится большинство показателей уровня жизни населения.

Показатели интенсивности – именованные величины.

3) средние величины. Необходимость расчета средних величин обусловлена сложностью социально-экономических явлений, которые с одной стороны устойчивы в своей массе, с другой стороны сугубо индивидуальны. Это связано с тем, что социально-экономические явления формируются под влиянием значительной совокупности факторов, одни из которых, называемые основными, формируют типический уровень признаков совокупности, другие (случайные) – обуславливают отклонение индивидуальных значений от типического уровня. В средних величинах происходит взаимопогашение влияния случайных факторов и средние величины выступают характеристикой типического уровня признака (то есть уровень признака, характерный для данной совокупности). Научной основой этой роли средних величин является Однокачественность и количественная однородность изучаемой совокупности.

Кетлер: «Статистическое среднее представляет собой категорию объективной действительности. Типическое среднее – истинная величина, отклонения от которой могут быть только случайными».

Виды средних величин:

1. степенные средние. Среднее арифметическое, среднее гармоническое, среднее геометрическое, среднее квадратическое, среднее кубическое, среднее четвертой степени (может и более высоких степеней).

2. структурные средние. Мода, медиана. Они называются структурными, так как их величина не зависит от значения признака у каждой единицы совокупности, а определяется составом (структурой) совокупности.

8. Типы средних, области их применения.

1. степенные средние. Среднее арифметическое, среднее гармоническое, среднее геометрическое, среднее квадратическое, среднее кубическое, среднее четвертой степени (может и более высоких степеней).

2. структурные средние. Мода, медиана. Они называются структурными, так как их величина не зависит от значения признака у каждой единицы совокупности, а определяется составом (структурой) совокупности.

Средняя гармоническая

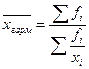
Средняя гармоническая используется для расчета среднего значения относительных величин при условии, что известен числитель исходной формулы усредняемого показателя.

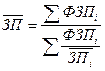
Средняя геометрическая

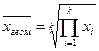
k - число сомножителей в подкоренном выражении

Степень корня = k

Средняя геометрическая используется для расчета средних темпов роста в анализе рядов динамики.

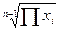- имеется в виду подсчет по всем единицам совокупности,

то есть k = n – 1.

Средняя квадратическая

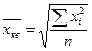(простая) → 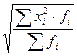(взвешенная)

Формула средней квадратической лежит в основе расчета дисперсии.

Свойства средней арифметической:

1. Произведение средней арифметической на сумму частот равно сумме произведения индивидуальных значений признака на соответствующие частоты.

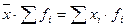
Среднее арифметическое – это значение признака, которое имела бы каждая единица совокупности при равномерном распределении общего объема признака совокупности.

1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю.

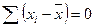
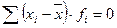
1. Сумма квадратов отклонений индивидуальных значений от средней величины всегда меньше суммы квадратов отклонений индивидуальных значений от любой другой произвольной величины.

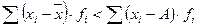
1. Если все индивидуальные значения увеличить или уменьшить на одну и ту же постоянную величину, то среднее арифметическое уменьшится или увеличится на эту же величину.
2. Если все частоты умножить или разделить на одно и то же постоянное число, то среднее не изменится.

9. Понятие вариации, показатели вариации.

Вариация – это различия в индивидуальных значениях признака у единиц совокупности. Вариация – основа развития различных систем (биологических, экономических).

От степени вариации признаков совокупности зависит типичность показателей центра распределения. Чем меньше вариация, тем в большей степени средняя выполняет роль характеристики типического уровня признака. Поэтому, как правило, расчет показателей центра распределения сопровождается расчетом показателей вариации.

Для оценки вариации существуют абсолютные и относительные показатели вариации.

Абсолютные показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

1. размах вариации. Разность между максимальным и минимальным значением признаков совокупности.

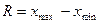
Характеризует на какую величину различаются между собой крайние значения изучаемого распределения.

Среднее линейное отклонение

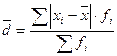, где

x_i - индивидуальное значение признака,

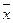- среднее значение по совокупности.

3. дисперсия

σ² =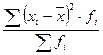

Показатель дисперсии в экономических исследованиях содержательно не интерпретируется, но благодаря своим свойствам широко используется в расчете многих статистических характеристик.

Виды выборки

1.Собственно-случайная выборка. Без предварительной подготовки генеральной совокупности случайно или механически из нее извлекают единицы в выборочную совокупность. В данном случае единица отбора совпадает с единицей наблюдения.

2.Стратифицированная типологическая (районированная) выборка. В генеральной совокупности выделяются типы или страты, а затем из каждого типа извлекается число единиц, пропорционально доли каждого типа в общем объеме генеральной совокупности. Единица отбора совпадает с единицей наблюдения.

3.Серийная выборка (гнездовая). В генеральной совокупности выбираются серии (гнезда) и в выборку случайно или механически производят отбор серий. Внутри серий, попавших в выборку, проводится сплошное наблюдение. Чаще всего используется для оценки качества продукции, товаров и в сельском хозяйстве.

4.Многоступенчатая выборка. Связана со сложностью социально-экономических явлений, что не позволяет на первом этапе сформировать окончательно выборочную совокупность. На каждом этапе меняется единица отбора.

5.Многофазная выборка. Каждая фаза отличается объемом программы наблюдения. Чем меньше объем выборки, тем шире программа наблюдения.

18. Cпособы отбора единиц в выборочную совокупность

1) Случайный отбор. Реализуется с использованием жеребьевки или таблиц случайных чисел.

2) Механический отбор. Частный случай случайного отбора. Реализуется через расчет шага отбора.

, где

N – объем генеральной совокупности,

n – объем выборки.

Пример: = - в выборку попадает каждая пятая единица генеральной совокупности.

19. Средняя и предельная ошибки выборки.

Репрезентативная выборка – выборка, которая позволяет получить так называемые несмещенные оценки параметров генеральной совокупности. Выборочную совокупность можно назвать репрезентативной, если распределение единиц в выборке соответствует распределению единиц генеральной совокупности.

При проведении любого наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При достаточно хорошей организации наблюдения этих ошибок можно избежать. При организации выборочного наблюдения возникают ошибки репрезентативности. Эти ошибки связаны не с организацией наблюдения, а с самой сутью выборочного исследования (по части, по выборочной совокупности, приходится судить о целом, о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что параметры выборочной совокупности (показатели, рассчитанные по выборке) не совпадают с параметрами (показатели генеральной совокупности). Задача исследователя: сформировать выборку, позволяющую получить минимальную ошибку и определить конкретную величину полученной ошибки. Теоретической основой определения ошибки репрезентативности являются теоремы Чебышева, Ляпунова и Бернулли.

Суть теоремы Чебышева: При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, близкой к 1, можно утверждать, что величина ошибки выборки не превысит сколь угодно малой положительной величины ε

n → ∞ , → 1 , где

- выборочная средняя;

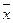- генеральная средняя;

P - вероятность события, заключенного в скобках.

Суть события в том, что ошибка чрезвычайно мала.

Теорема Чебышева доказывает принципиальную возможность оценки параметров генеральной совокупности на основе выборочных данных. Исходя из этой теоремы не ясно, чему равна ошибка выборки и с какой именно вероятностью можно гарантировать непревышение конкретной величины ошибки. На эти вопросы отвечает теорема Ляпунова.

Суть теоремы Ляпунова.

При неограниченном увеличении числа наблюдений в генеральной совокупности с ограниченной дисперсией вероятность того, что ошибка выборки не превысит величины, равна нормированной функции Лапласа.

n → ∞ , , где

μ- средняя ошибка выборки.

, где

- средняя выборочная по i-ой выборке.

n - число выборок.

Данная формула на практике не может быть использована, так как неизвестна величина генеральной средней и фактически проводится всегда лишь одна выборка.

Математической статистикой доказано, что μ² прямо пропорциональна дисперсии генеральной совокупности и обратно пропорциональна объему выборки.

, где

σ² – генеральная дисперсия.

Между величинами выборочной и генеральной дисперсий существует зависимость:

, где

S² – выборочная дисперсия.

При большом объеме выборки сомножитель

Поэтому на практике его игнорируют и в расчете средней ошибки используют величину выборочной дисперсии.

t·μ = Δ - предельная ошибка выборки.

- нормированное отклонение

- нормированное отклонение выборочной средней от генеральной среденей.

Теорема Ляпунова доказывает, что при большом объеме выборки распределение ошибки выборки подчинено закону нормального распределения.

Для нормального распределения составлены таблицы, в которых зафиксировано отношение t и уровня вероятности.

Задавая уровень вероятности, по таблицам находится соответствующее значение нормированного отклонения. Социально-экономические исследования чаще всего проводятся с вероятностью p = 0.954, t = 1.96 ≈ 2

p = 0.997 , t ≈ 3.

Если задана p = 0.954 , то Δ = 2·μ

Доверительный интервал:

В условиях большой выборки распределение ошибки выборки подчиняется закону нормального распределения. Поэтому, задавая уровень вероятности, величину t (значение нормированного отклонения) находят по таблице нормированной функции Лапласа.

Выше указанные формулы расчета ошибки выборки разработаны для повторного отбора. В статистике понятие повторного и бесповторного отбора соответствует понятиям возвратного и безвозвратного шара в теории вероятности. Повторный отбор заключается в том, что единица генеральной совокупности, изъятая в выборку, возвращается назад в генеральную совокупность и может быть повторно выбрана в выборочную совокупность. Бесповторный отбор – отобранная из генеральной совокупности единица не возвращается назад.

При повторном отборе на протяжении всего отбора сохраняется неизменная вероятность попадания единицы в выборку p = 1/N

При бесповторном отборе вероятность изменения от для первой единицы отбора до для последней единицы отбора.

Поэтому формула средней ошибки выборки для бесповторного отбора, который, как правило, используется в анализе социально-экономических явлений, имеет вид

20. Влияние вида выборки и способа отбора на величину ошибки выборки

Ошибка выборки есть всегда, это связано с самой сутью выборочного наблюдения. Величина ошибки выборки зависит также от вида выборки. В формуле средней ошибки при реализации различных видов выборки используются разные дисперсии.

При проведении любого наблюдения возникают ошибки наблюдения, которые могут быть случайными и преднамеренными. При достаточно хорошей организации наблюдения этих ошибок можно избежать. При организации выборочного наблюдения возникают ошибки репрезентативности. Эти ошибки связаны не с организацией наблюдения, а с самой сутью выборочного исследования (по части, по выборочной совокупности, приходится судить о целом, о генеральной совокупности). Ошибка выборки неизбежна и состоит в том, что параметры выборочной совокупности (показатели, рассчитанные по выборке) не совпадают с параметрами (показатели генеральной совокупности). Задача исследователя: сформировать выборку, позволяющую получить минимальную ошибку и определить конкретную величину полученной ошибки. Теоретической основой определения ошибки репрезентативности являются теоремы Чебышева, Ляпунова и Бернулли

21. Определение доверительных интервалов для генеральной средней и генеральной доли.

Теорема Бернулли – это частный случай теоремы Чебышева и теоремы Ляпунова. Она является основой расчета ошибки выборки для доли. То есть при изучении альтернативного признак или так называемой дихотомической переменной (имеющей всего два исхода). Реально это оценивается в расчете доли единиц совокупности, обладающих или не обладающих данным признаком.

При расчете средней ошибки доли используется формула, аналогичная средней ошибке средней величины, но с учетом дисперсии доли.

, где

W - выборочная совокупность (доля);

p - доля генеральной совокупности.

σ² = W · (1 – W) - дисперсия доли.

W – tμ ≤ p ≤ W + tμ

Между величинами выборочной и генеральной дисперсий существует зависимость:

, где

S² – выборочная дисперсия.

При большом объеме выборки сомножитель

Поэтому на практике его игнорируют и в расчете средней ошибки используют величину выборочной дисперсии.

t·μ = Δ - предельная ошибка выборки.

- нормированное отклонение

- нормированное отклонение выборочной средней от генеральной среденей.

Теорема Ляпунова доказывает, что при большом объеме выборки распределение ошибки выборки подчинено закону нормального распределения.

Для нормального распределения составлены таблицы, в которых зафиксировано отношение t и уровня вероятности.

Задавая уровень вероятности, по таблицам находится соответствующее значение нормированного отклонения. Социально-экономические исследования чаще всего проводятся с вероятностью p = 0.954, t = 1.96 ≈ 2

p = 0.997 , t ≈ 3.

Если задана p = 0.954 , то Δ = 2·μ

Доверительный интервал:

В условиях большой выборки распределение ошибки выборки подчиняется закону нормального распределения. Поэтому, задавая уровень вероятности, величину t (значение нормированного отклонения) находят по таблице нормированной функции Лапласа.

22. Расчет объема выборки.

На стадии проектирования выборочного наблюдения рассчитывается объем выборки, который позволит получить допустимую величину ошибки, то есть ошибку, которая удовлетворит задачам исследования. Расчет объема выборки осуществляют исходя из формулы ошибки выборки. Предельная ошибка выборки:

, , ,

Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования.

Значение t зависит от устанавливаемого уровня вероятности. Значение дисперсии берется по результатам предшествующих аналогичных исследований, если таковые проводились и если за время между исследованиями не произошло существенных изменений в изучаемой совокупности.

Может быть проведено пробное исследование и по результатам его рассчитана величина дисперсии. Но очень часто нет средств на проведение пилотажного (пробного) исследования.

К определению дисперсии подходят формально, исходя их привила трех σ - когда невозможно провести пилотажные исследования.

σ = 1/6 R , где R – размах вариации.

Если распределение заведомо асимметрично, то значение σ = 1/5 R

В формуле расчета объема выборки ( ) ошибка выборки берется как

абсолютная величина, однако, на практике размер ошибки задается, как правило, как относительная величина. То есть говорят, что ошибка не должна превышать 2% (или 5%).

→

23. Малая выборка: понятие, особенности.

При использовании больших выборок, сформированных из больших генеральных совокупностей, величина ошибки выборки подчиняется нормальному закону, который устанавливает связь между величиной вероятности и значением t.

Если анализируемая выборка малого объема, то распределение ошибок выборки не подчиняется нормальному закону распределения. Поэтому проблема малой выборки длительное время оставалась нерешенной.

Проблема малой выборки была решена английским математиком и статистиком по фамилии Госсет, который вошел в историю под псевдонимом Стьюдент.

1908 г – доказал, что распределение ошибок в условиях малой выборки подчиняется особому закону распределения, который и получил его имя – t-распределение Стьюдента.

Распределение Стьюдента, как и нормальное распределение, симметрично, однако ветви кривой распределения Стьюдента медленнее приближаются к оси абсцисс. То есть вероятность появления больших отклонений от средней величины в распределении Стьюдента выше, чем в нормальном распределении.

По t-распределению Стьюдента составлены таблицы, в которых (в отличии от нормального распределения) вероятность связана не только с величиной t, но и с числом степеней свободы, которое определяется

d.f. = n – 1 (n – объем совокупности)

При объеме выборки n ≥ 100 значения в таблицах нормального распределения и распределения Стьюдента полностью совпадают, при 30 ≤ n ≤ 100 - расхождения незначительные, при n < 30 - существенные расхождения.

Безусловно малой выборкой считается выборка объемом меньше 30 единиц. Поэтому при работе с выборками таких объемов в формуле предельной ошибки выборки используется величина t из таблицы t-распределения Стьюдента.

В формуле расчета средней ошибки выборки мы не можем игнорировать сомножитель, корректирующий величину выборочной дисперсии.

- в условиях малой выборки

, где

S - выборочная дисперсия.

То есть дисперсия делится не на объем выборки, а на число степеней свободы.

24. Проверка существенности различий между выборочными средними

Проверка различий осуществляется на основе t- статистики.ьПроверка нулевой гипотезы Но:

,

где выборочная средняя первой выборки равна средней по второй выборке

Проверка на основе t-статистики означает оценку отношений оцениваемой величины к стандартной ошибке.

, где

, среднеквадратичная ошибка

Оценка генеральной дисперсии по двум выборкам

Оценка гипотезы по результатом расчетов t-статистики:

Если t_расч.< t_табл, то принимается нулевая гипотеза о равенстве средних величин, то есть расхорждение между ними случайно,

Если t_расч.> t_табл, то гипотеза отвергается, выборочные средние не равны, расхождение неслучайно.

25. Виды связей: функциональная, статистическая, корреляционная.

Все в этом мире взаимосвязано. Чтобы управлять социально-экономическими процессами и явлениями, необходимо знать наличие, направленность, силу связи между явлениями или признаками.

Существуют два вида связей:

Коэффициент корреляции

Исторически первым показателем тесноты связи был парный коэффициент корреляции, предложенный Пирсоном. Он основан на сопоставлении вариации признака-фактора и признака-результата.

cov =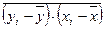

Среднее значение произведения отклонений индивидуальных значений результативного признака от своего среднего называется ковариацией (показатель оценивает совместное изменение двух признаков).

Однако показатель ковариации сложно содержательно комментировать. Нормированное значение показателя ковариации – это парный показатель корреляции Пирсона.

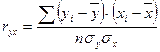
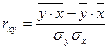
Достоинства коэффициента корреляции: величина изменяется по модулю от нуля до единицы. Близость коэффициента к нулю свидетельствует об отсутствии корреляционной зависимости. Близость к единице – о тесной корреляционной зависимости.

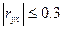- связь практически отсутствует;

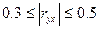- связь заметная;

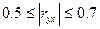- связь умеренная;

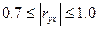- связь заметная.

Парный коэффициент корреляции – си