Модифицированные методы Эйлера

Пример 1.Применим первый модифицированный метод Эйлера для решения задачи Коши 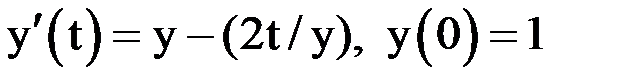, рассмотренной ранее в предыдущем примере. Возьмем шаг 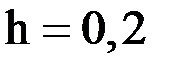. Тогда 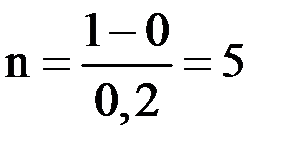, и расчетная формула первого модифицированного метода Эйлера имеет вид: 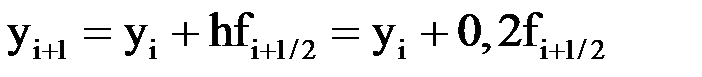, где

, ,

, .

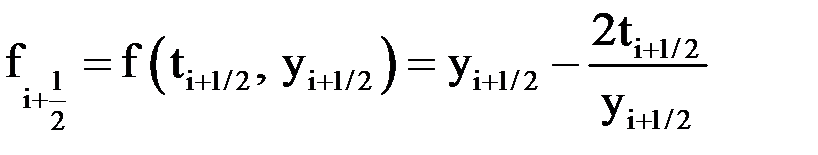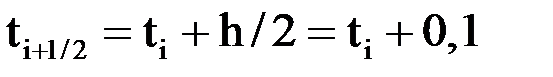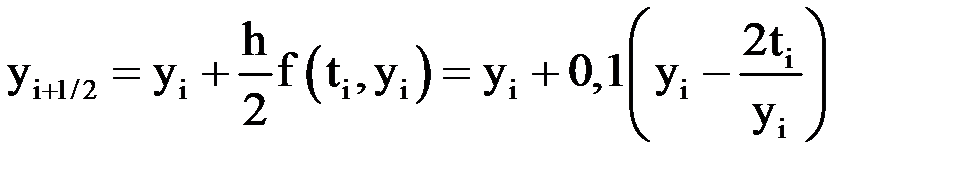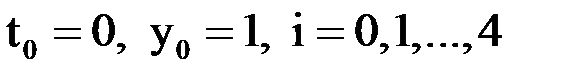Решение представим в виде таблицы.

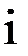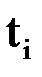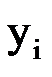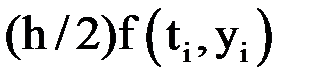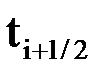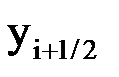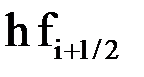			0,1	0,1	1,1	0,1836
	0,2	1,1836	0,0850	0,3	1,2682	0,1590
	0,4	1,3426	0,0747	0,5	1,4173	1,1424
	0,6	1,4850	0,0677	0,7	1,5527	0,1302
	0,8	1,6152	0,0625	0,9	1,6777	0,121
		1,7362

Третий столбец таблицы содержит приближенное решение 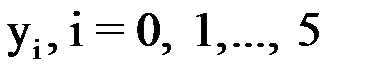. Сравнивая полученное приближенное решение с точным решением, представленном в таблице, видим, что погрешность составляет

.

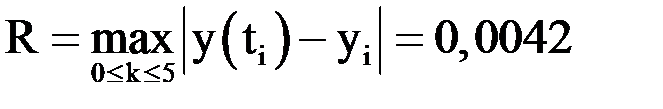Пример 2.Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши 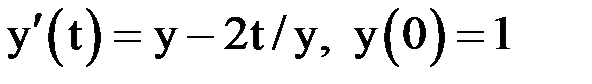, рассмотренной ранее в примере 1. Так же, как и ранее, зададим шаг 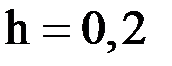. Тогда

.

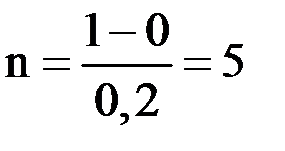В соответствии с данными формулами получим расчетную формулу метода Эйлера – Коши:

,

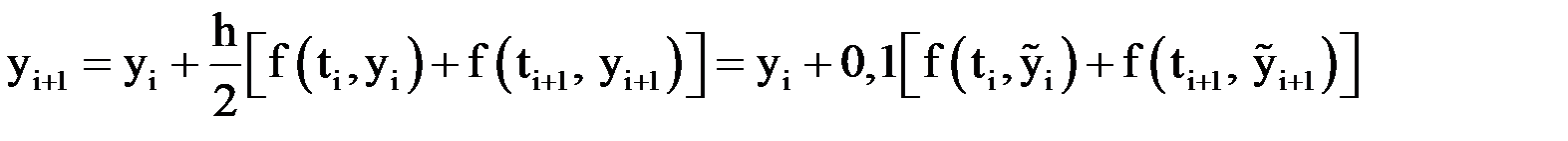где , , , , .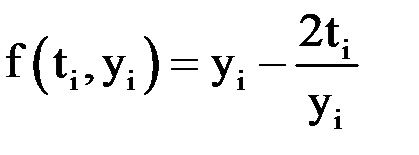

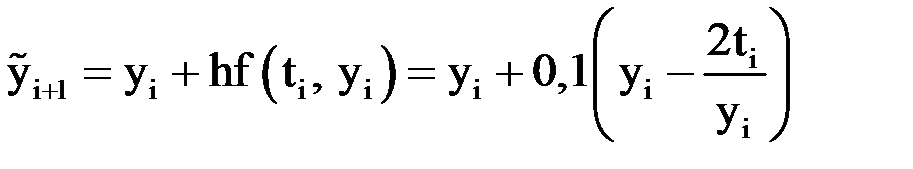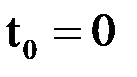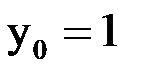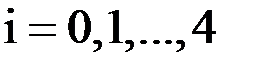Решение представим в виде таблицы.

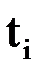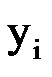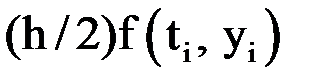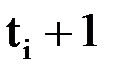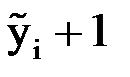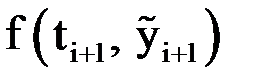			0,1	0,2	1,2	0,867
	0,2	1,1867	0,0850	0,4	1,3566	0,767
	0,4	1,3484	0,0755	0,6	1,4993	0,699
	0,6	1,4938	0,0690	0,8	1,6180	0,651
	0,8	1,6272	0,0645		1,7569	0,618
		1,7542

Таблица заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы содержит приближенное решение .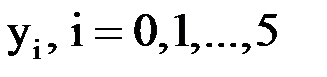

Сравним полученное приближенное решение с точным решением. Видим, что погрешность составляет .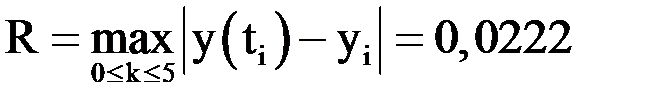

Метод Рунге-Кутты для решения задачи Коши

Методом Рунге-Кутты четвертого порядка точности найдем решение на отрезке 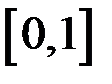следующей задачи Коши .

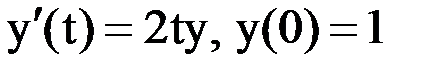Возьмем шаг 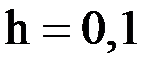. Тогда .

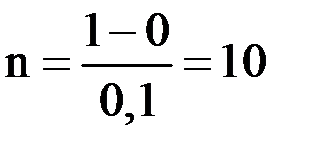Расчетные формулы имеют вид:

, , ,

, , .

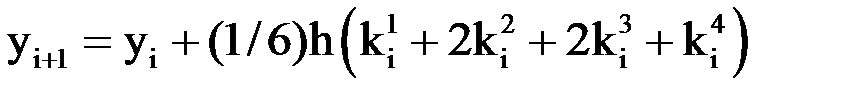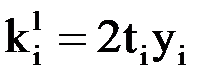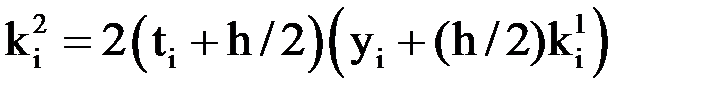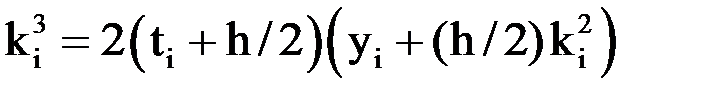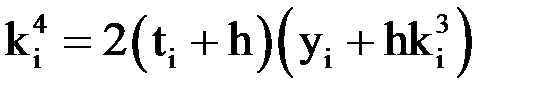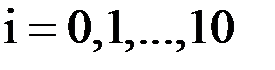Задача имеет точное решение: 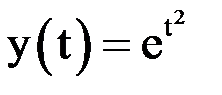, поэтому погрешность определяется как абсолютная величина разности между точными и приближенными значениями .

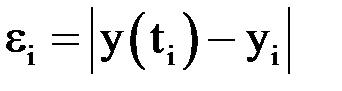Найденные приближенные значения решения 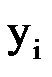и их погрешности 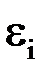представлены в таблице.

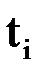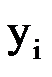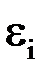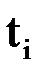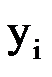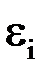			0,6	1,43333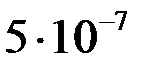
0,1	1,01005	10-9	0,7	1,63232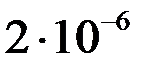
0,2	1,04081		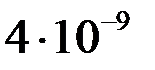0,8	1,89648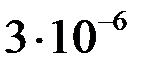
0,3	1,09417		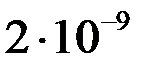0,9	2,2479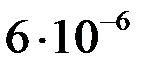
0,4	1,17351		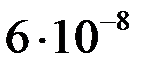	2,71827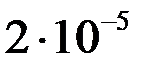
0,5	1,28403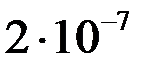

Решение краевой задачи методом прогонки

Методом прогонки решить краевую задачу:

.

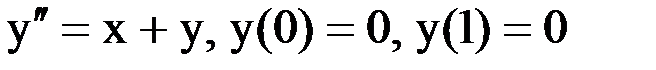Решение. Пусть .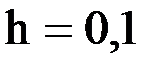

;

;

; ;

.

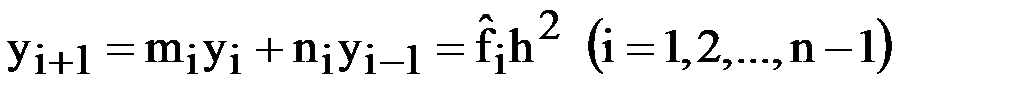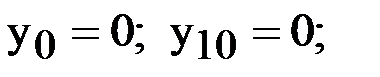
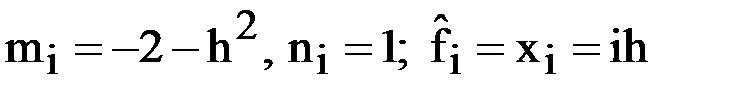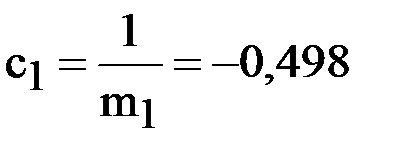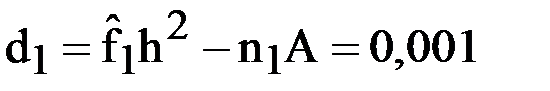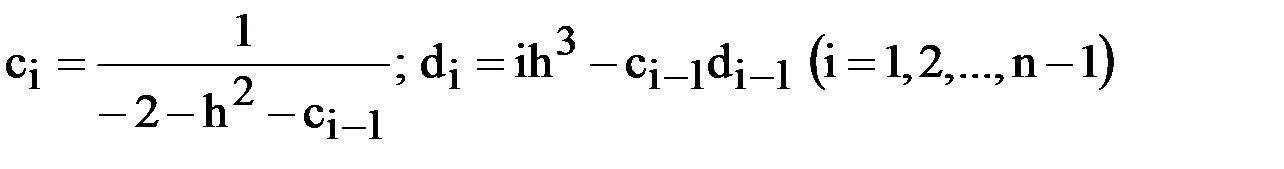Найденные значения 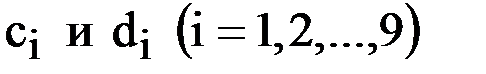записываем в первых двух строках таблицы. Используя известное значение 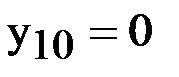, вычислим 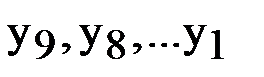и запишем в таблицу. Для значения в последней строке даны значения точного решения .

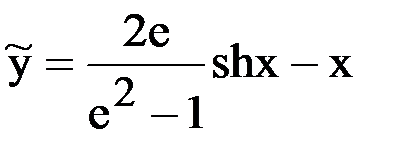Таблица 10

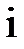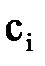		-0,498	-0,662	-0,878	-0,890	-0,900
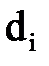		0,001	0,002	0,004	0,008	0,012
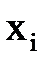		0,1	0,2	0,3	0,4	0,5
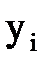		-0,025	-0,049	-0,072	-0,078	-0,081
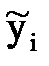		-0,015	-0,029	-0,041	-0,050	-0,057

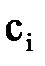	-0,908	-0,915	-0,921	-0,926
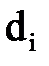	0,16	0,022	0,028	0,035
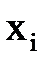	0,6	0,7	0,8	0,9
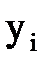	-0,078	-0,070	-0,055	-0,032
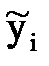	-0,058	-0,054	-0,044	-0,026

Литература

1. Бахвалов, Н.С. Численные методы в задачах и упражнениях [Электронный ресурс]: учебное пособие / Н.С. Бахвалов, А.В. Лапин, Е.В. Чижонков. - 3-е изд. (эл.). - М.: БИНОМ. Лаборатория знаний, 2013. - 240 с. - Режим доступа: http://www.studentlibrary.ru/book/ISBN9785996322664.html. – ЭБС "Электронная библиотека технического ВУЗа".

2. Численные методы [Электронный ресурс] / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. - 7-е изд. (эл.). - М.: БИНОМ. Лаборатория знаний, 2012. - 636 с. - Режим доступа: http://www.studentlibrary.ru/book/ISBN9785996308026.html. – ЭБС "Электронная библиотека технического ВУЗа".

3. Коломоец, А. А. Численные методы и комплексы программ [Текст]: учеб. пособие по курсу "Математическое моделирование" для студ. всех спец. / А. А. Коломоец, М. А. Дергачева; М-во образования и науки Рос. Федерации, Саратовский гос. техн. ун-т. - Саратов: СГТУ, 2011. - 64 с. – Экземпляров всего: 3. Имеется электронный аналог печатного издания.

4. Коломоец, А. А. Численные методы и комплексы программ [Электронный ресурс]: учеб. пособие / А. А. Коломоец, М. А. Дергачева; М-во образования и науки Рос. Федерации, Саратовский гос. техн. ун-т. – Электрон. текстовые дан. – Саратов: СГТУ, 2011. – 1 эл. опт. диск (CD-ROM). – Систем. требования: 128 МБ ОЗУ ; 4х CD-ROM дисковод; Microsoft Office 2003 и выше; ПК Pentium III или выше. - Загл. с экрана. – б. ц.
Электронный аналог печатного издания. Диск помещен в контейнер 14х12 см. Режим доступа: http://lib.sstu.ru/books/zak 52_11.pdf.

5. Покровский В.В. Электромагнетизм. Методы решения задач [Электронный ресурс]: учебное пособие/ Покровский В.В. – Электрон. текстовые данные. – М.: БИНОМ. Лаборатория знаний, 2011. – 120 c. – Режим доступа: http://www.studentlibrary.ru/book/ISBN9785996306411.html. – ЭБС «"Электронная библиотека технического ВУЗа»

6. Григорьев А.Д. Методы вычислительной электродинамики [Электронный ресурс]/ Григорьев А.Д. – Электрон. текстовые данные. – М.: ФИЗМАТЛИТ, 2012. – 432 c. – Режим доступа: http://www.iprbookshop.ru/33386. – ЭБС «IPRbooks».

ПРИЛОЖЕНИЯ

Приложение 1

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Саратовский государственный технический университет имени Гагарина Ю.А.»

Кафедра «Автоматизированные электротехнологические установки и системы»

Контрольная работа по дисциплине

«Численные методы решения задач электродинамики

И тепломассопереноса»

Вариант №

Выполнил: ст-т гр. б1ЭЛЭТ-21

Иванов И.И.

№ зач. книжки

Проверил: к.т.н., доцент каф. АЭУ

Алексеев В.С.

Саратов - 2015

Приложение 2

Варианты заданий

1. Решить уравнение методом половинного деления, хорд с точностью .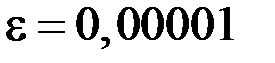

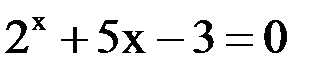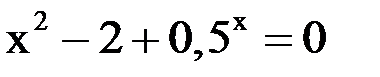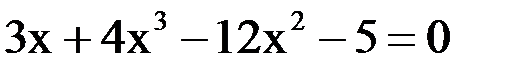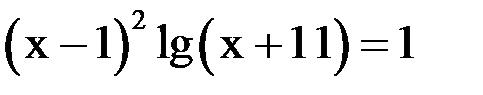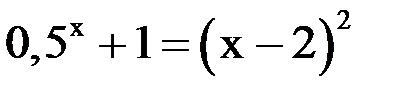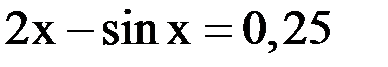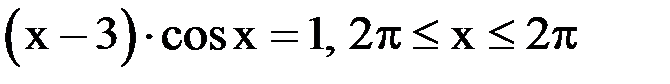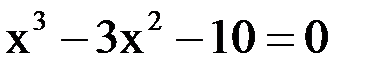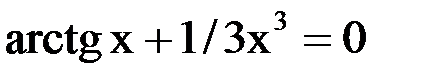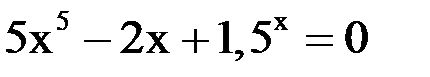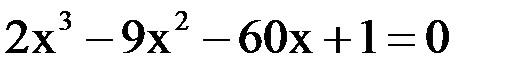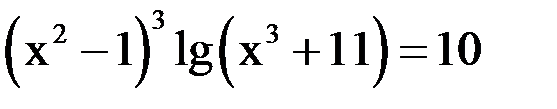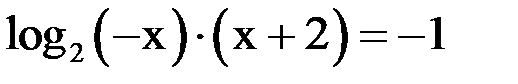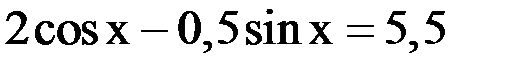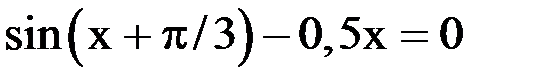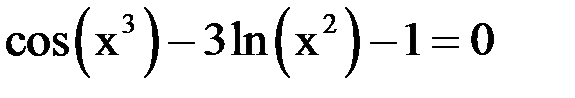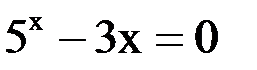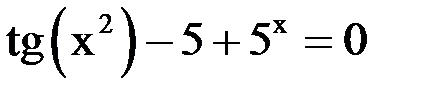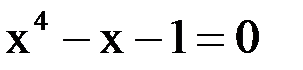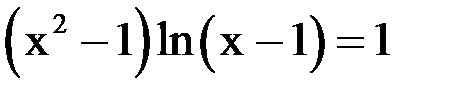2. Решить уравнение методом Ньютона и итерации с точностью .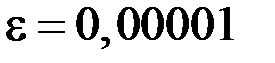

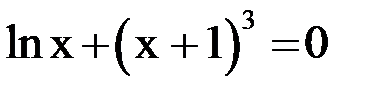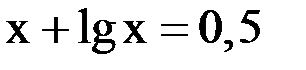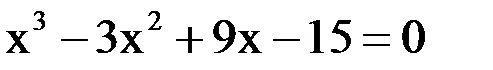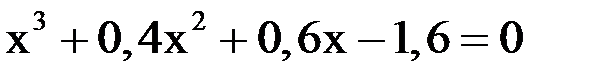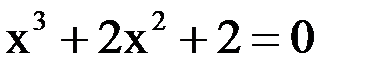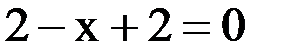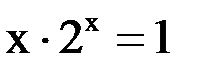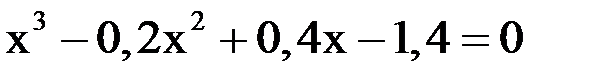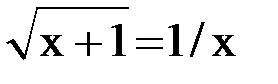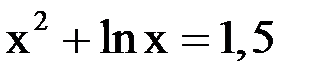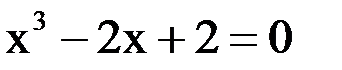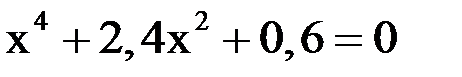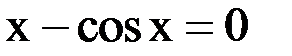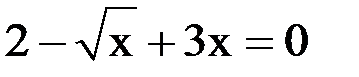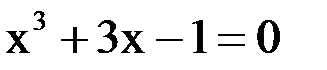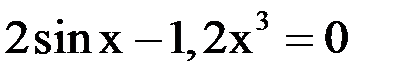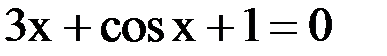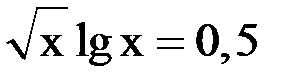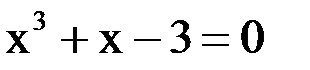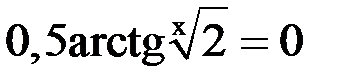3. Решить уравнение методом хорд и касательных и видоизменённым Ньютона с точностью .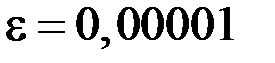

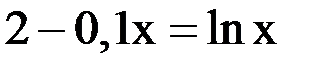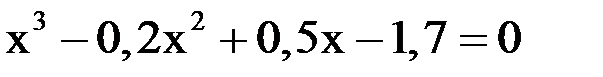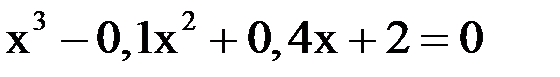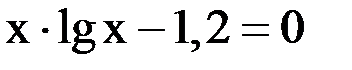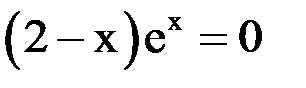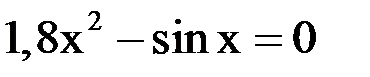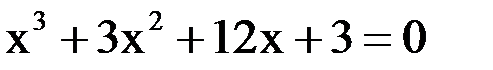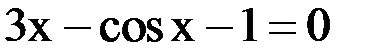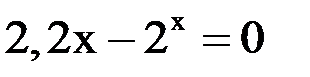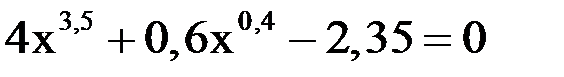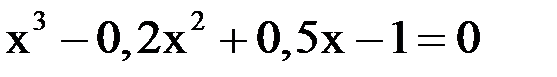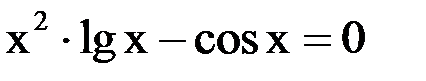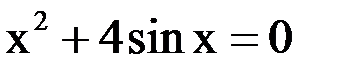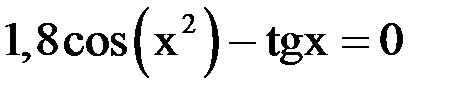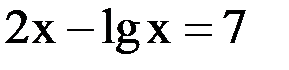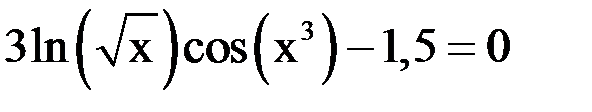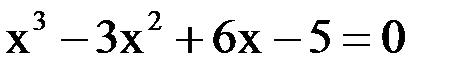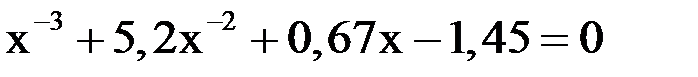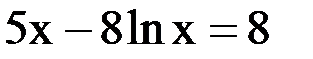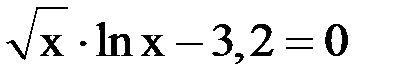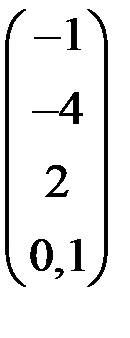
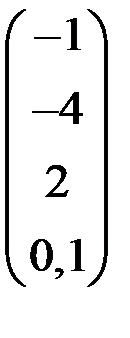
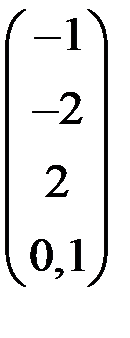
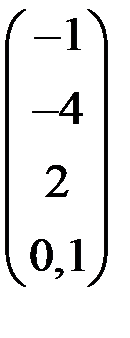
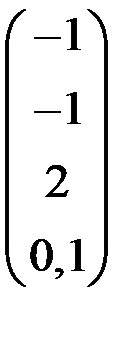
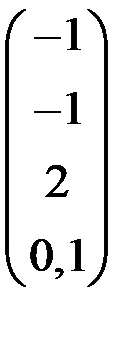
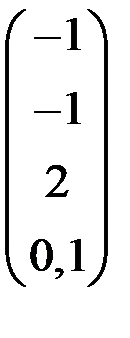
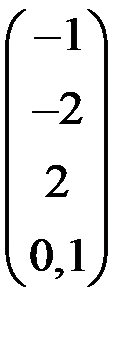
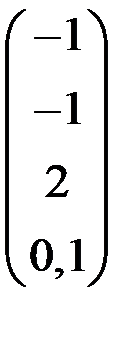
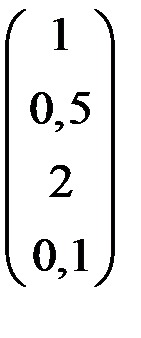
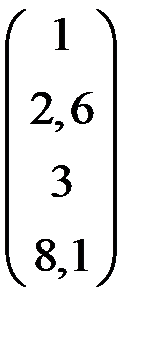
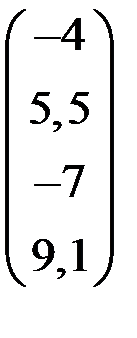
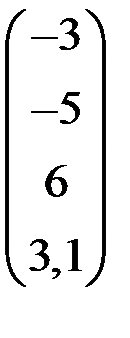
4. Решить систему 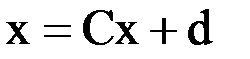методом простой итерации с точностью .

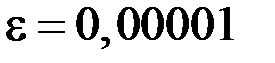	С	d		С	d

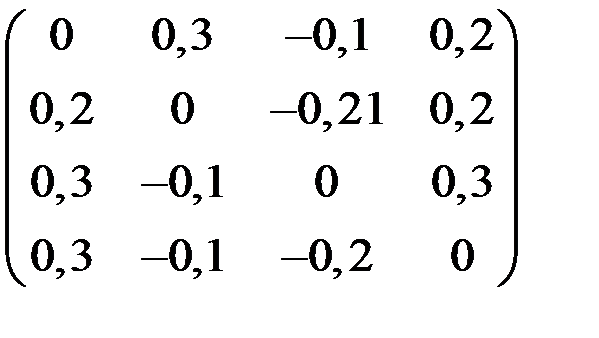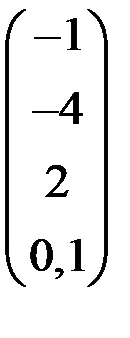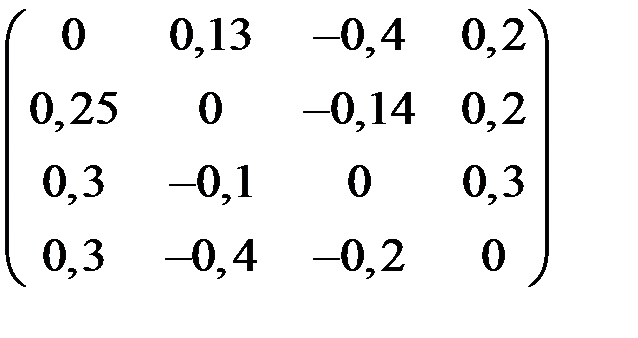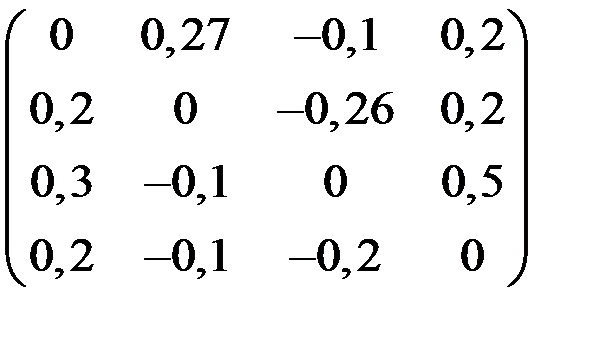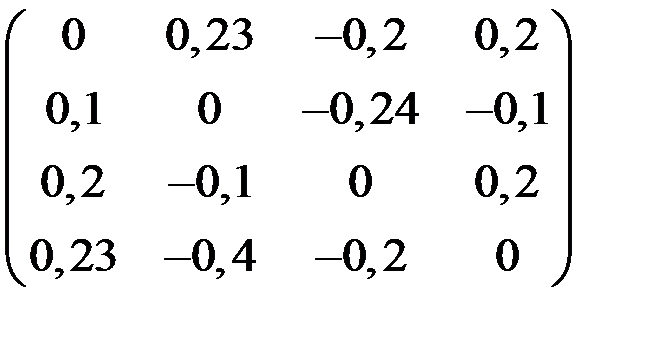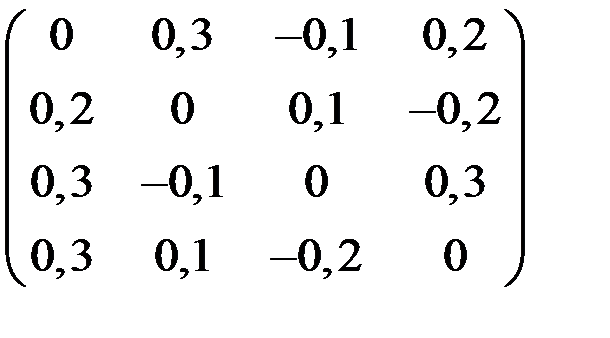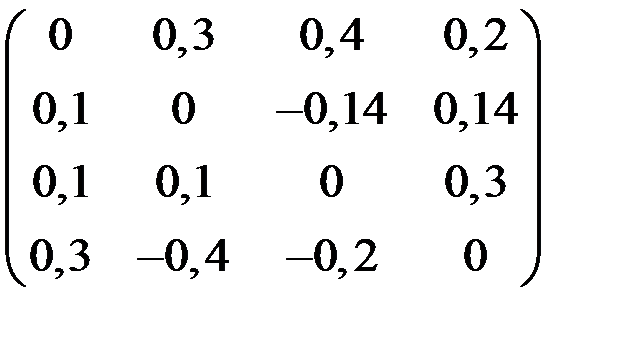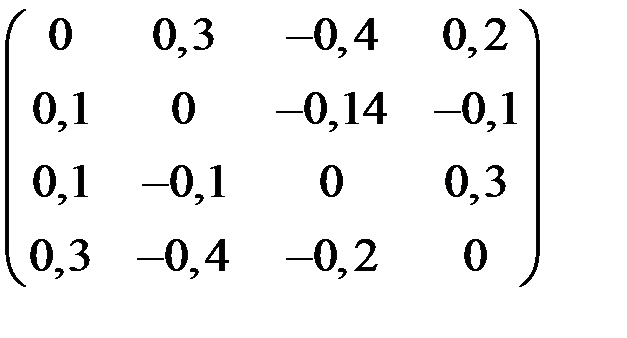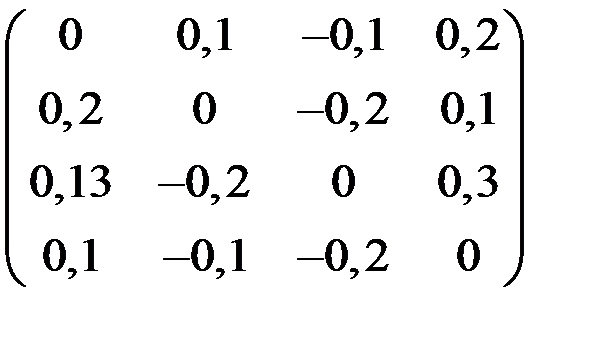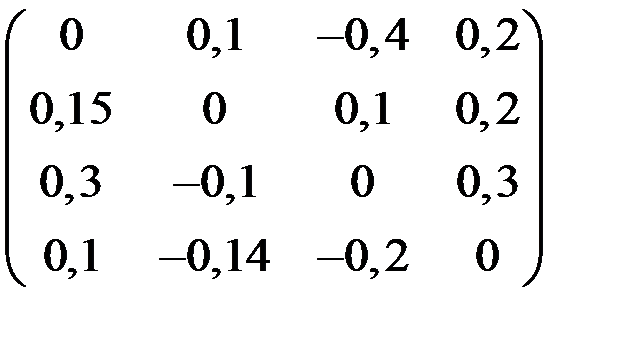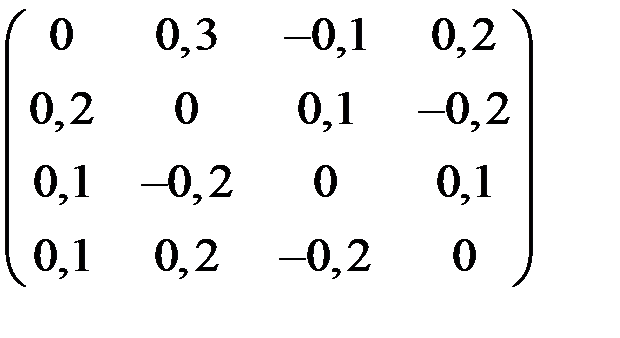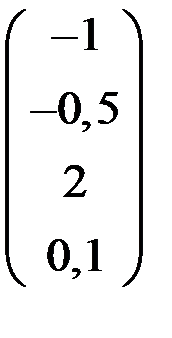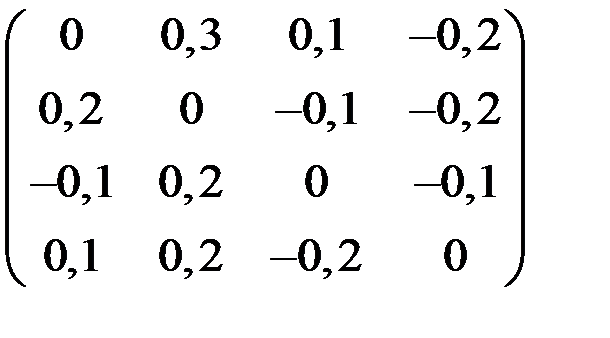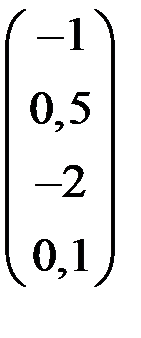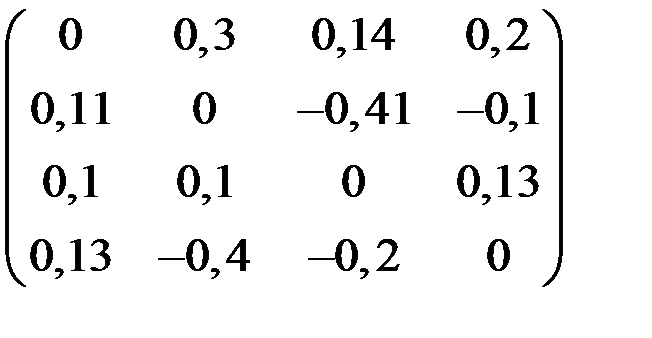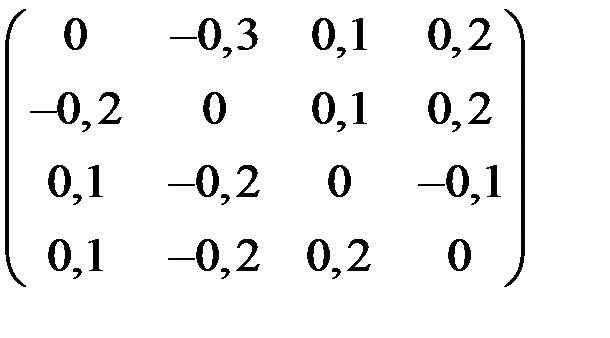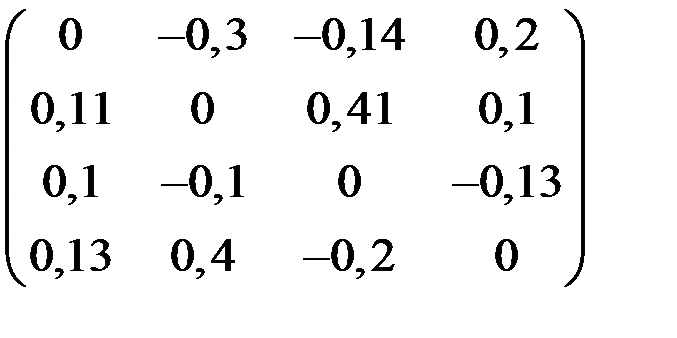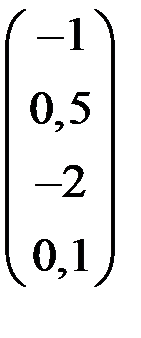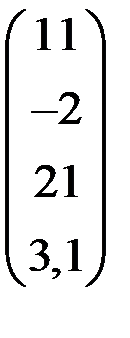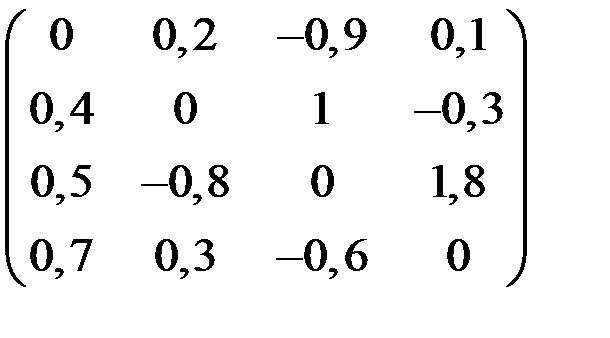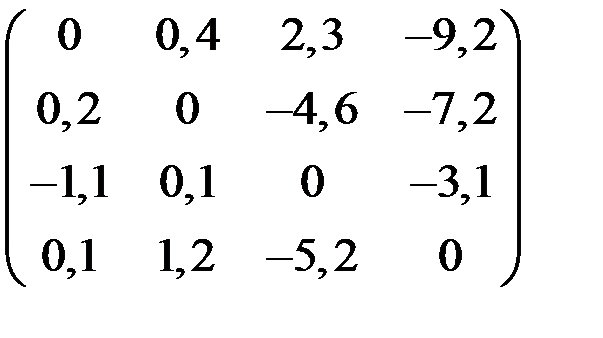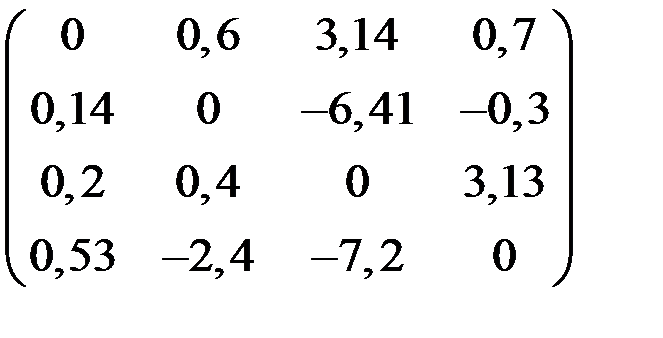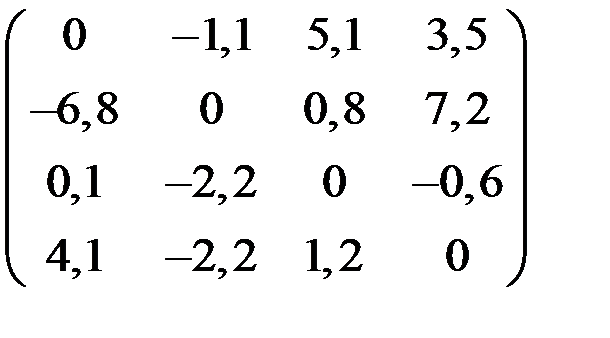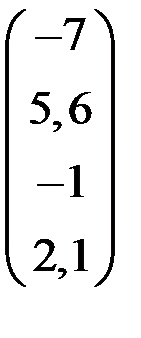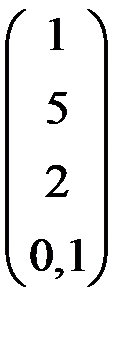
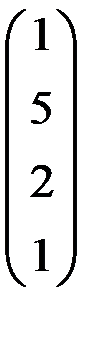
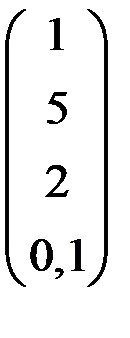
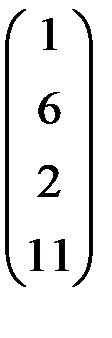
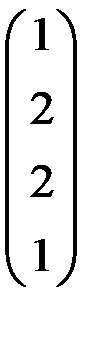
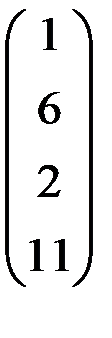
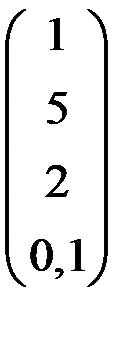
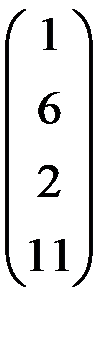
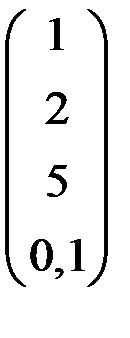
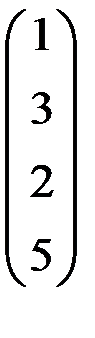
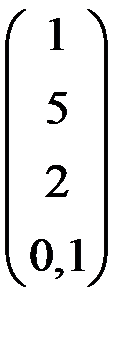
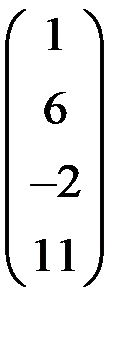
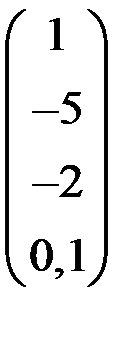
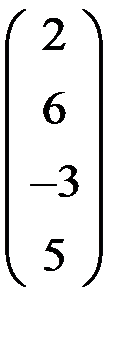
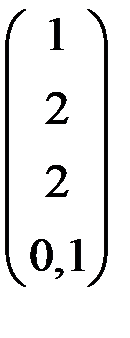
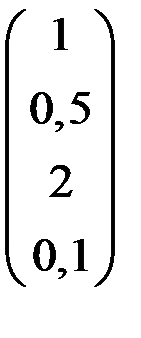
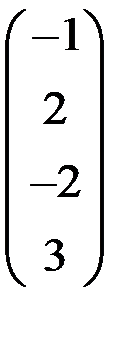
5. Решить систему 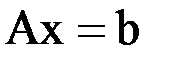методом Зейделя с точностью .

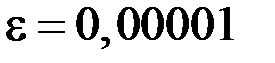	А	b		A	b

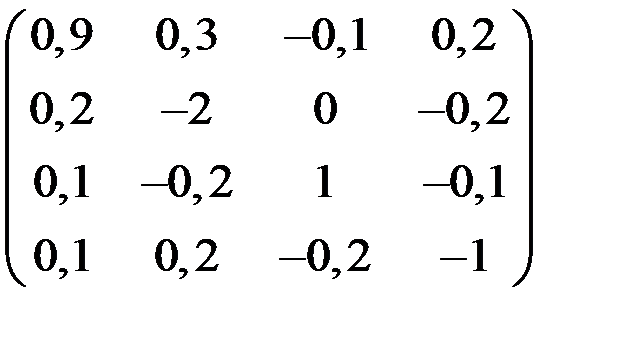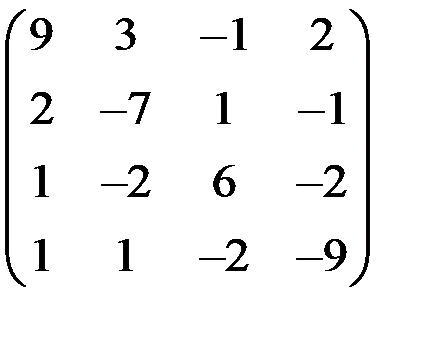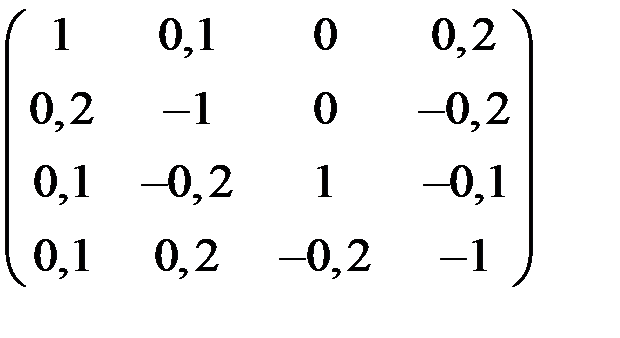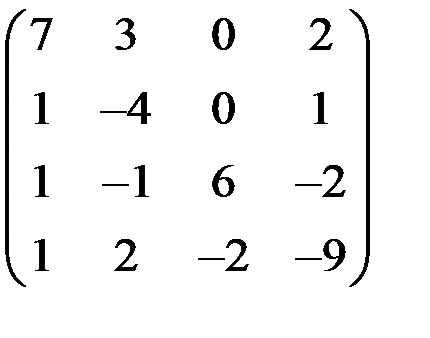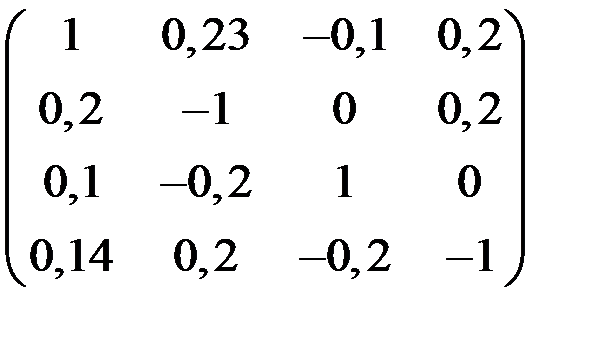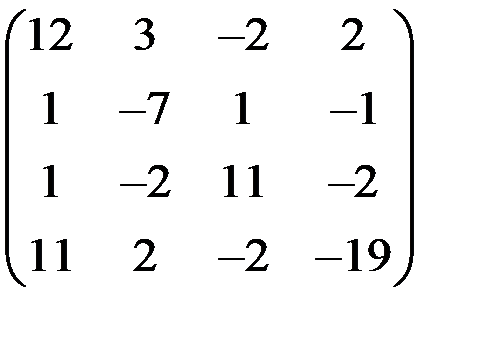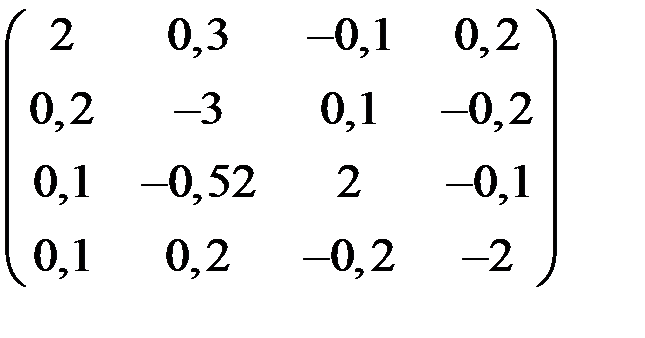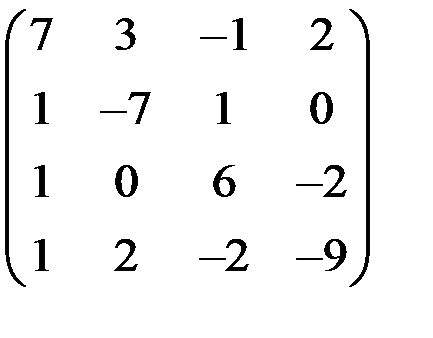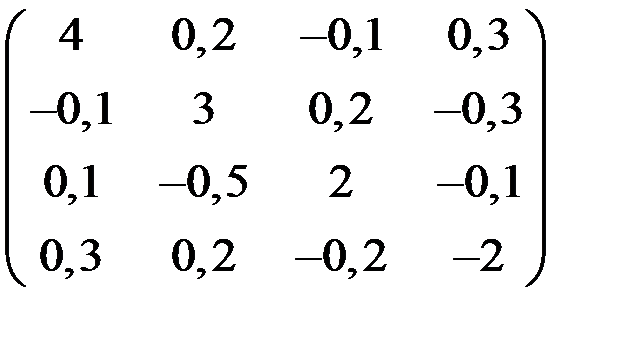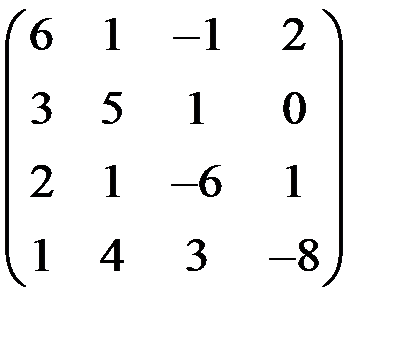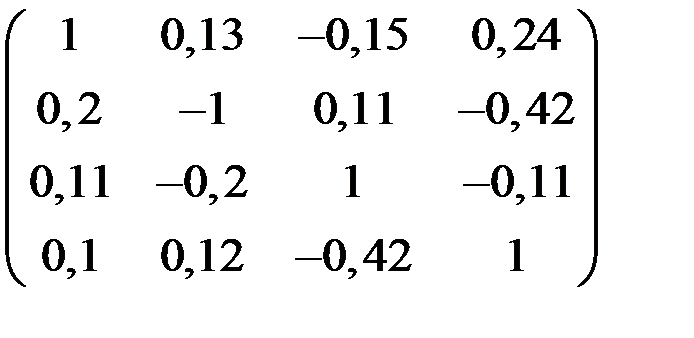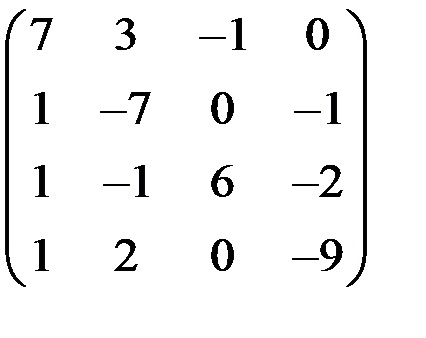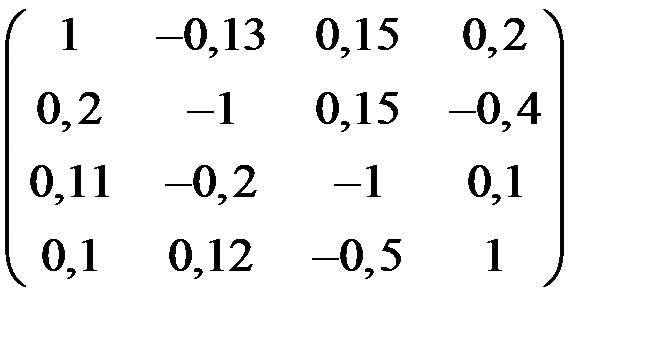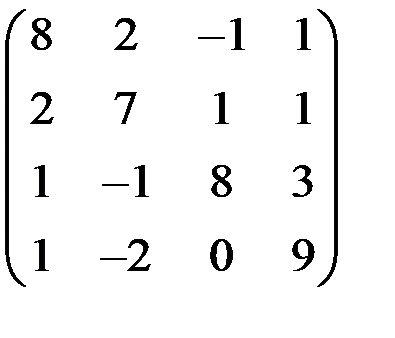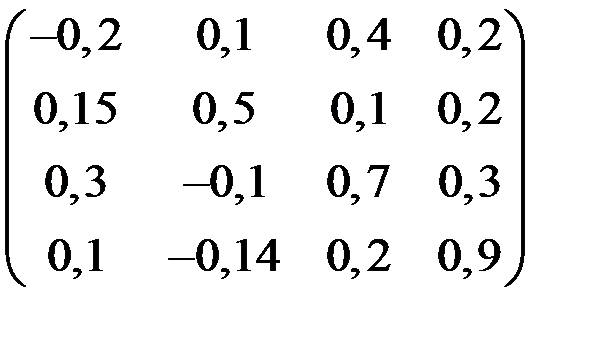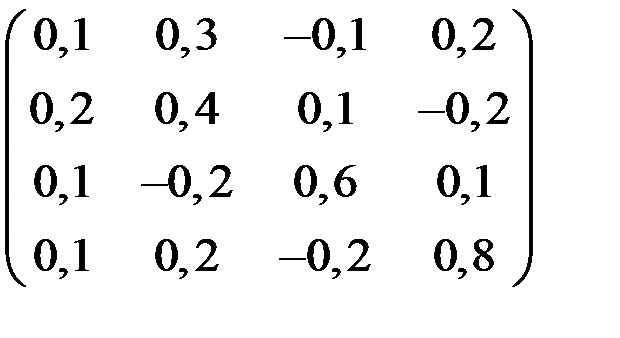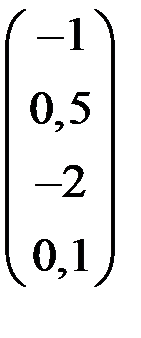6. Решить систему методом простой итерации с точностью .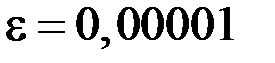

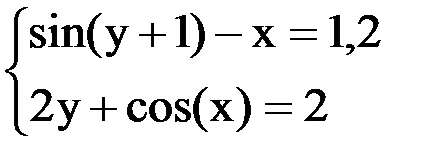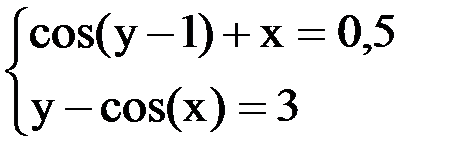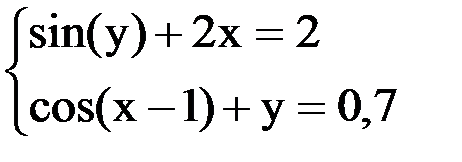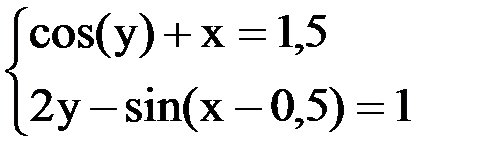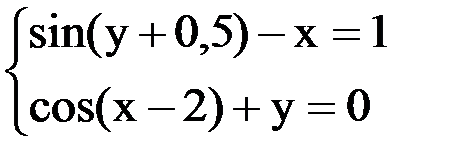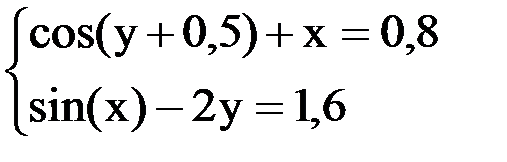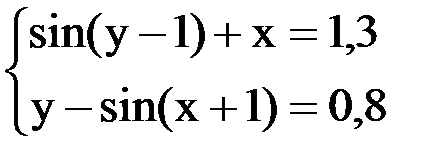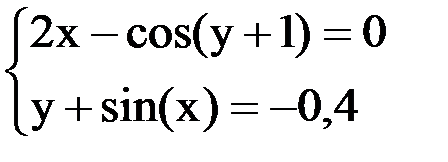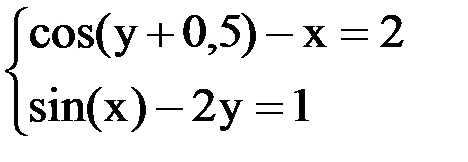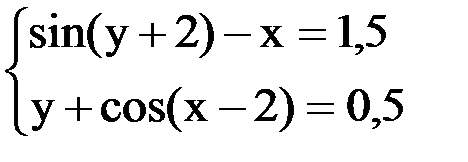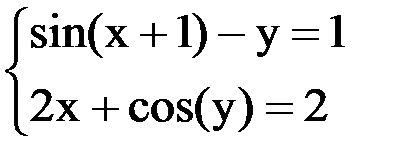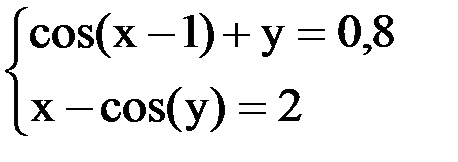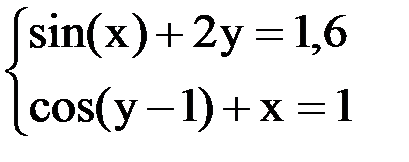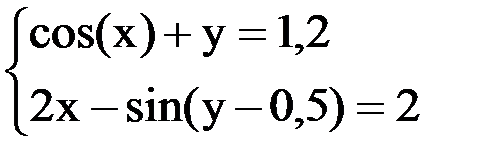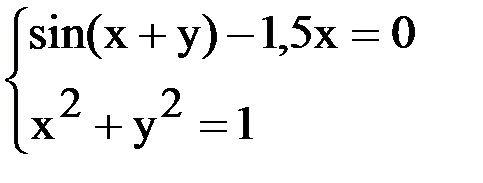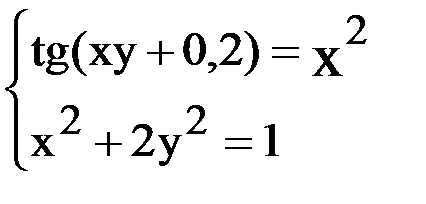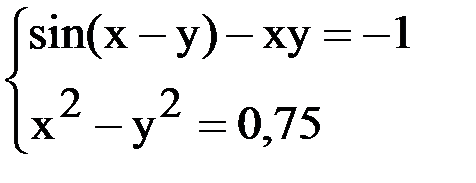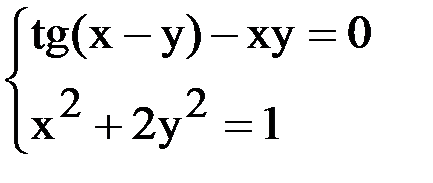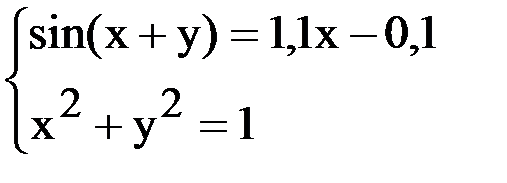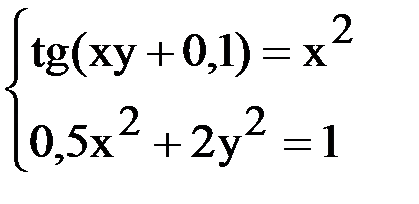7. Решить систему методом Ньютона с точностью .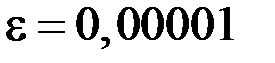

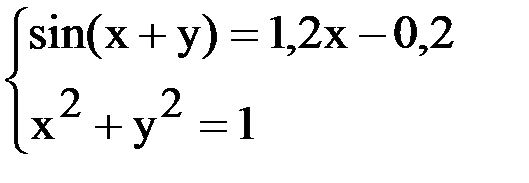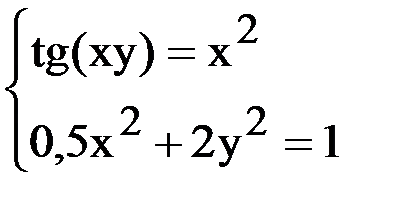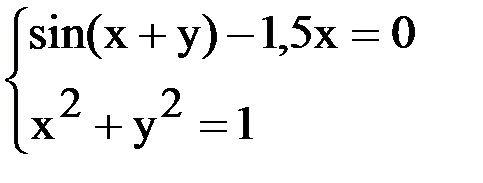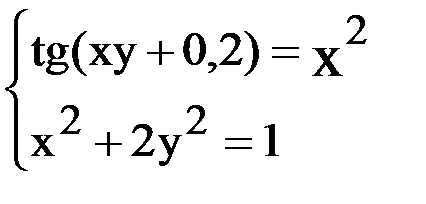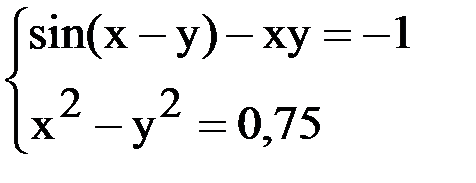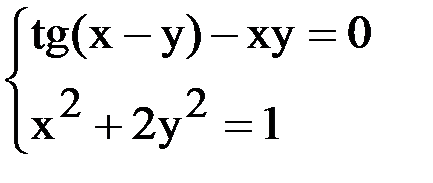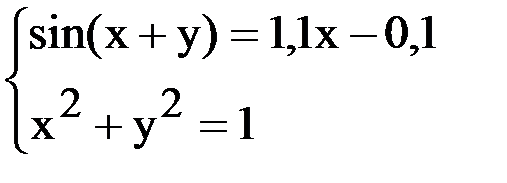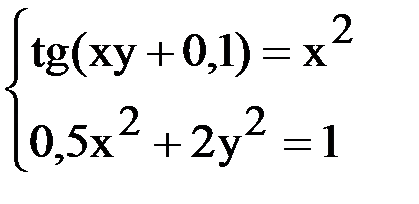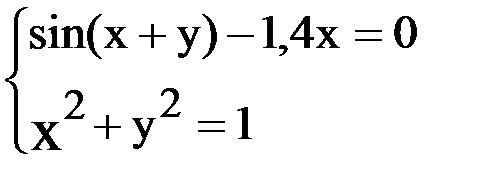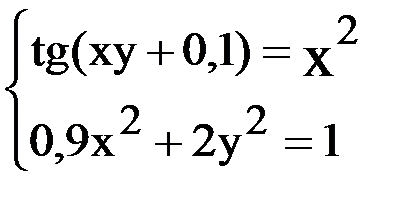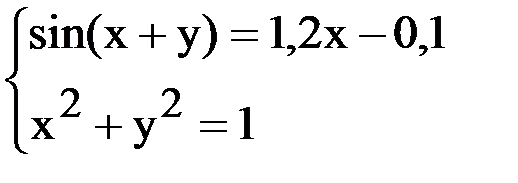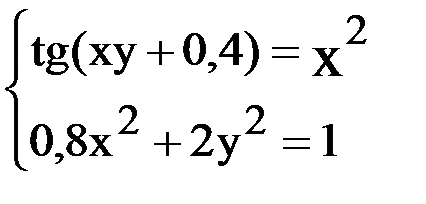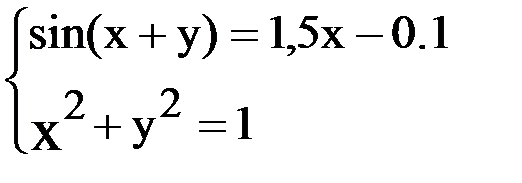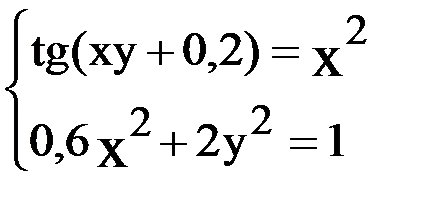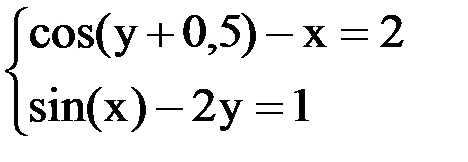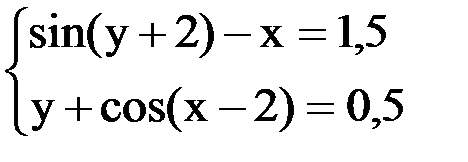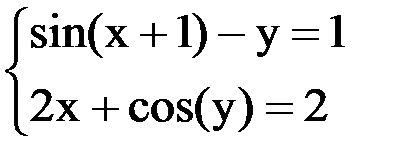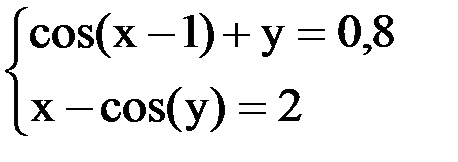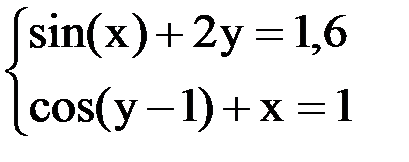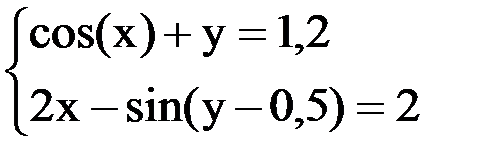8. По заданным значениям 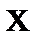и 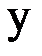найти прямую 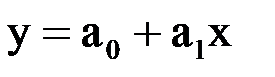и параболу 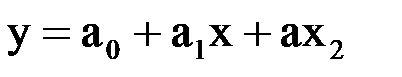методом наименьших квадратов. Найти погрешность. Построить прямую и кривую в той же системе координат, где нанесены данные точки.

№15

N
X
Y

№16

N
X		0,12	0,14	0,16	0,18	0,2	0,22	0,24	0,26	0,28
Y	-1			1,1	1,3	-0,5	-0,3	0,5	0,7	1,5

№17

N
X
Y						2,5		3,3	2,8

№18

N
X
Y	-5	-3,5	-5,3	-4	-6	-3,8	-4,3	-5,1	-4,8

№19

N
X
Y			-1		0,5	-0,15	-0,06	0,18	0,15	0,2

№20

N
X
Y

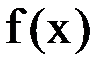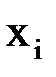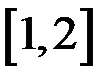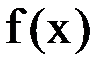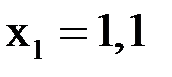9. 1) Заданы значения функции в узлах , получающиеся делением отрезка на 5 частей. Найти значения функции при и 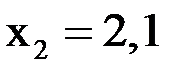с помощью интерполяционных формул Ньютона.

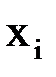0,1	1,0	1,1	0,9	0,9	0,8	1,1	1,0	1,2	1,2	1,1	0,8	0,8	0,8	1,1	3,5	0,2	2,1	0,3	1,5	0,6
1,2	2,1	2,2	2,0	1,9	2,0	2,2	2,1	1,8	2,0	1,9	2,0	2,2	1,8	2,2	4,1	0,7	3,3	0,4	4,5	0,8
1,4	2,9	3,2	3,0	3,2	2,9	3,2	3,1	3,2	3,0	3,2	2,8	2,9	2,9	3,0	5,3	0,8	4,5	0,5	6,2	0,9
1,6	3,8	4,2	3,8	3,8	4,2	4,2	3,8	4,1	3,8	3,8	4,0	4,0	4,0	4,1	6,8	0,9	5,7	0,6	7,8	1,4
1,8	5,2	5,2	5,1	5,1	5,2	5,1	5,2	5,2	5,0	4,9	5,2	5,2	4,9	4,9	7,2	1,0	6,9	1,2	8,4	1,6
2,0	5,9	6,0	5,8	6,1	5,8	5,9	6,2	6,1	6,1	5,8	6,0	5,8	6,1	5,9	8,4	1,3	8,1	1,5	9,9	2,3

2) Заданы значения 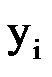функции 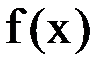в точках 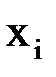. Найти значение функци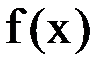и при 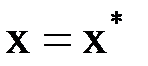. Задачу решить с помощью интерполяционного многочлена Лагранжа.
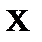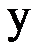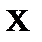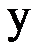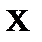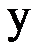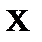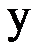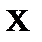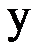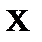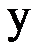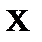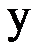
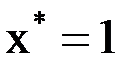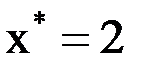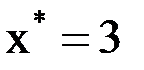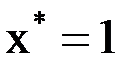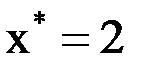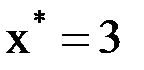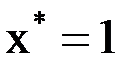
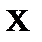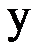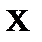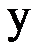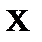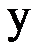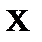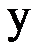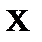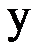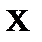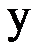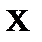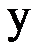
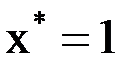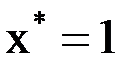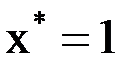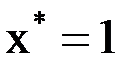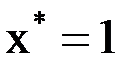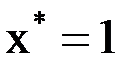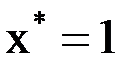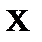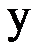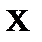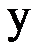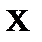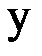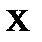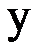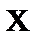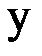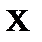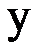
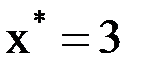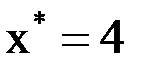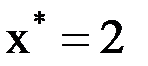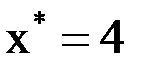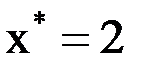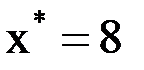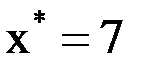