Введем параметры для решения ЗЛП.

· Установим флажок Неотрицательные значения и флажок Линейная модель.

· Нажимаем кнопку ОК. Опять появится диалоговое окно Поиск решения.

· Нажимаем кнопку выполнить. В результате на экране появится диалоговое окно Результаты поиска решения (рис.1. 18.).

Рис. 1.18. Решение найдено

Ответ. Распределение товара по торговым точкам приведено на рис. 18 Общие затраты на перевозку продукции составят 1330 денежных единиц.

1.4. Задача о назначениях

В процессе управления производством зачастую возникают задачи назначения исполнителей на различные виды работ, например: подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами научно-технического развития, распределение экипажей самолетов между авиалиниями.

Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Требуется так распределить работы между рабочими, чтобы общие затраты на выпол­нение всех работ были минимальными.

Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ. Пусть т — количество работ.

Обозначения:

— показатель эффективности назначения i-го рабочего на j-й работе, например издержки выполнения i-м рабочим j-й работы;

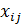— переменная модели ( 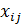= 1, если i-й рабочий используется на j-й работе, и 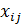= 0 в противном случае).

Модель задачи о назначениях:

, (1.26)

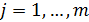, , (1.27 а)

, , (1.27 б)

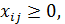
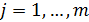; . (1.28)

Здесь (1.26)— целевая функция (минимум издержек на выполнение всех работ);

(1.27)— система ограничений, отражающая следующие условия:

а) каждая работа должна быть выполнена одним рабочим;

б) каждый рабочий может быть привлечен к одной работе;

(1.28)— условия неотрицательности переменных.

При решении задачи о назначениях исходной информацией является таблица задачи о назначениях элементами которой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов:

Таблица 1.4

Работа   Рабочий	1	2	…	j	...	m
1			…		…
2			…		…
...	…	…	…	…	…	…
j			…		…
...	…	…	…	…	…	…
m			…		…

Результатом решения задачи о назначениях (1.26)— (1.28) является вектор

компоненты которого — целые числа.

Пример 3.Задача о назначениях.

Администрация мясокомбината при­няла на работу пять человек. Каждый из них имеет различные способности и навыки и затрачивает различное время на выпол­нение определенной работы. Необходимо выполнить пять видов работ. Время выполнения работы каждым работником приведено в табл. 1.5.

Таблица 1.5

Работник	Время выполнения работы, ч

Требуется назначить на каждый вид работы одного из работ­ников. Как это нужно сделать, чтобы общее время, необходимое для завершения всех видов работ, было минимальным?

Решение.