Открытая транспортная задача.

а) 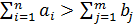- — излишек продукта

Способ сведения к замкнутой задаче. Пусть 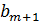— величина избытка продукции, т.е. 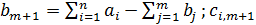- штраф за единицу продукта, не реализованного в пункте i; у_i — количество продукта, не реализованного в пункте i.

Замкнутая транспортная задача имеет вид

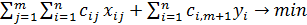, (1.11)

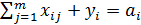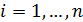, , (1.12)

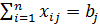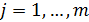, , (1.13)

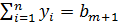, (1.14)

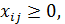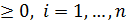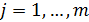у_i ; . (1.15)

б) 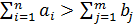— дефицит продукта.

Способ сведения к замкнутой задаче. Пусть 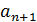— величина дефицита продукции, т.е.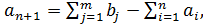 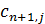- штраф за еди­ницу продукта, недопоставленного в пункт j; 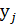— количество продукта, недопоставленного в пункту.

Замкнутая транспортная задача имеет вид

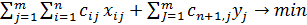, (1.16)

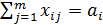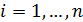, , (1.17)

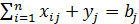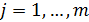, , (1.18)

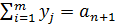, (1.19)

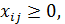
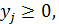
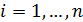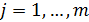; . (1.20)

3. Транспортная задача с запретами. Пусть Е — множество пар индексов (ij), таких, что из пункта i в пункт j допускается транспортировка продукта. Между любыми другими двумя пунктами транспортировка не допускается.

Пусть М— большое число, например

, , .

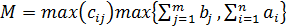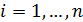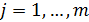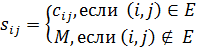
Тогда в оптимальном плане 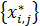транспортной задачи 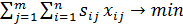при ограничениях (1.8)—(1.1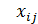0) = 0, .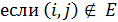

4. Транспортная задача с фиксированными перевозками. Если объем перевозок между пунктам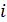и и 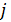задан, то в задаче (1.7)—(1.10) вводится дополнительное ограничени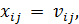е: где 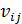— заданный объем перевозок.

5. Транспортная задача с ограничениями на пропускную способность. Если объем перевозок из пункта i в пункт j ограничен величиной 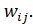, то в задаче (1.7)—(1.10) вводится дополнительное ограничение: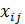

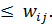
6. Транспортная задача с фиксированными доплатами. Предположим, что в открытой транспортной задаче имеет место дефицит продукта и для его устранения в пунктах 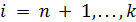возможно создание новых мощностей .

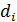Пусть переменные 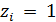, если в пункте 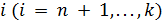вводятся мощности d_i и 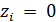, если в пункте i мощности не вводятся. Издержки на ввод мощностей d, в пункте i (i = n + 1, ..., k)составляют и_i.

С учетом возможности создания новых мощностей транспорт­ная задача может быть записана в следующем виде:

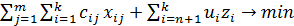, (1.21)

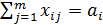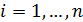, , (1.22)

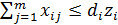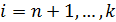, , (1.23)

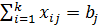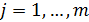, , (1.24)

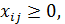
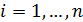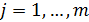; . (1.25)

Здесь (1.21)— целевая функция (минимум затрат на транспортировку и ввод мощностей);

(1.22) — ограничения по величине предложения в каждом су­ществующем пункте производства;

(1.23) — ограничения по величине предложения в каждом новом пункте производства;

(1.24) — ограничения по величине спроса в каждом пункте по­требления;

(1.25) — условия неотрицательности объемов перевозок.

Помимо непрерывных переменных 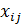в модель включены булевы переменные 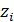. Задача (1.21)— (1.25) является задачей линейного программирования со «смешанными» переменными.

Все приведенные модели описывают транспортную задачу в виде задачи линейного программирования. В такой форме она может быть решена стандартными средствами линейного программирования, например симплекс-методом.

Для решения транспортной задачи могут быть использованы также и менее трудоемкие (по объему вычислений) алгоритмы, например метод потенциалов.

Большинство специальных алгоритмов решения транспортной задачи использует исходную информацию в форме транспортной таблицы:

Таблица 1.1

Пункт потребления Пункт производства			…	j	...	m	Пред- ложе- ние
			…		...
			…		...
…	...	...	...	...	...	...	...
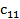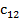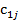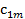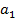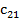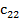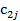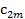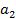i			…		...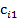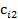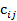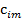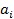
...	...	...	...	...	...	...	...
n			…		...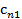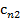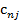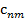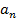
Спрос			...		...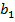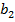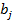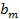

Оптимальный план перевозок имеет вид

Таблица 1.2

Пункт потребления Пункт производства			…	j	...	m
			…		...
			…		...
…	...	...	...	...	...	...
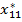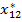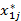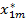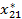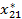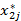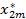i			…		...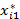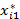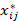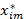
...	...	...	...	...	...	...
n			…		...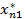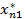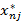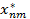

Пример 2.Задача организации оптимального снабжения.

Три фермерских хозяйства 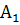, , 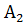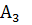ежедневно могут доставлять в город соответственно 180, 220 и 100 ц молока для обеспечения пяти торговых точек: 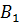, , 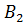, , 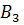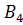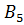.Стоимость перевозки 1 ц молока и потребности торговых точек в молоке указаны в табл. 1.3.

Таблица 1.3

.

Фермерские хозяйства	Затраты на перевозку 1ц к торговым точкам	Запас молока, ц
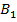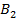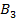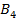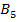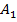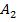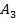Потребности в молоке, ц

Определить оптимальный план поставки молока в каждую точ­ку для удовлетворения потребностей, чтобы суммарные транспорт­ные издержки были минимальными.

Решение. Так как целевая функция и неравенства-ограниче­ния линейны, эта задача является задачей линейного программи­рования. Данная задача яв­ляется транспортной задачей закрытого типа, так как запасы молока у поставщиков (фермерских хозяйств) равны потребно­стям в молоке у торговых точек. Для задачи открытого типа меняется изменяется вид системы ограничений.

Математическая модель задачи

Переменные: 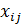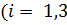; 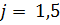) — количество молока, поставля­емое 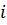-м фермерским хозяйством в 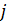-ю торговую точку.

Целевая функция — суммарные транспортные издержки, кото­рые необходимо минимизировать:

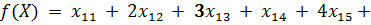
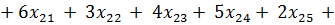
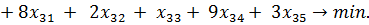
Функциональные ограничения:

• по поставщикам

,

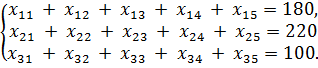•по потребителям

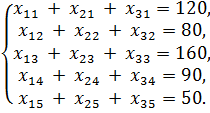
Прямые ограничения: .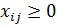

1.Укажем адреса ячеек, в которые будет помещен результат решения. Изменяемые ячейки — B11:F13. В эти ячейки в резуль­тате решения задачи будут записаны оптимальные значения .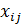

2.Введем исходные данные. Введите исходные данные задачи, как показано на рис. 1.14.

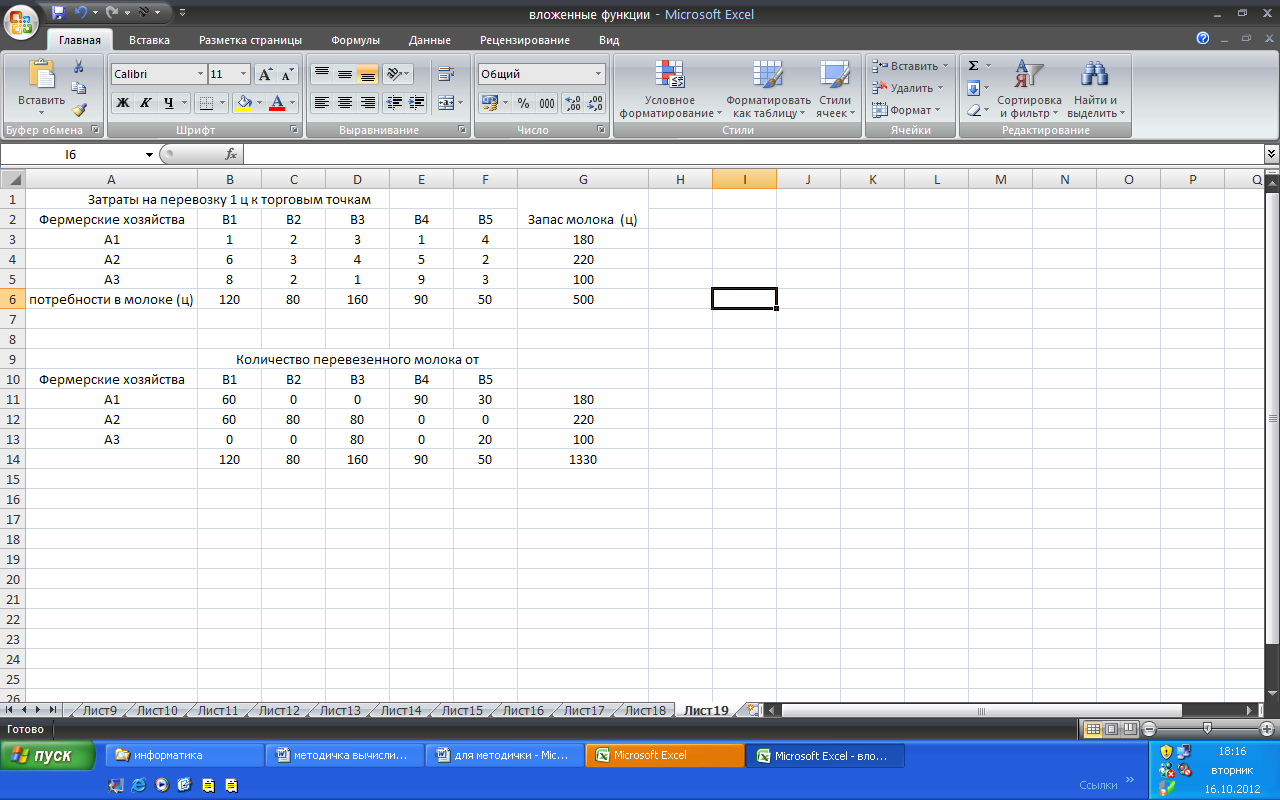
Рис. 1.14. Введены исходные данные

3. Введем зависимости для ограничений. Сначала введем условия реализации мощностей поставщиков:

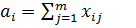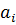где — мощность поставщика 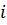; 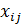— объем поставки груза от по­ставщика 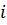к потребителю 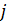; 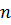— количество потребителей.

· Поместим курсор в ячейку G11.

· Выберем функцию СУММ.

· Выделим необходимые для суммирования ячейки B11:F11.

· Нажмем кнопку ОК для подтверждения ввода формулы для суммирования

Содержимое ячейки G11 скопируем в ячейки G12, G13.

Затем введите условия удовлетворения запросов потребителей:

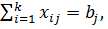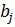где — мощность потребителя у; 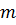— количество поставщиков.

· Поместим курсор в ячейку В14.

· Выберем функцию СУММ.

· Выделим необходимые для суммирования ячейки В11: В13.

· Нажмем кнопку ОК для подтверждения ввода формулы для суммирования.

Содержимое ячейки В14скопируем в ячейки С14 и F14.

4.Введем зависимость для целевой функции. Для вычисления значения целевой функции, соответствующей минимальным сум­марным затратам на доставку груза, зарезервируем ячейку и вве­дем формулу для ее вычисления:

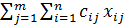, где 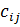— стоимость доставки 1 ц молока от поставщика к потреби­телю .

· Поместим курсор в ячейку G14 (после решения задачи в данной ячейке будет находиться значение целевой функции).

· Запускаем Мастер функций (значок f_x). ■

· В окне Категория выбираем Математические.

· В окне Функция выбираем СУММПРОИЗВ.

· Нажимаем кнопку ОК.

· В окне СУММПРОИЗВ укажем адреса массивов, элементы кото­рых обрабатываются этой функцией.

В нашей задаче целевая функция представляет собой произве­дение затрат на доставку молока (ячейки B3:F5) и объемов поста­вок для каждого потребителя (содержимое ячеек В11:F13).

· В поле Массив 1 указываем адреса B3:F5. В поле Массив 2 укажите адреса B11:F13.

· Нажимаем кнопку ОК — подтверждение окончания ввода адресов массивов.

В поле ячейки G14 появится некоторое числовое значение, равное произведению поставок на коэффициенты затрат по до­ставке грузов (в данной задаче — это число 0, рис. 1.15).

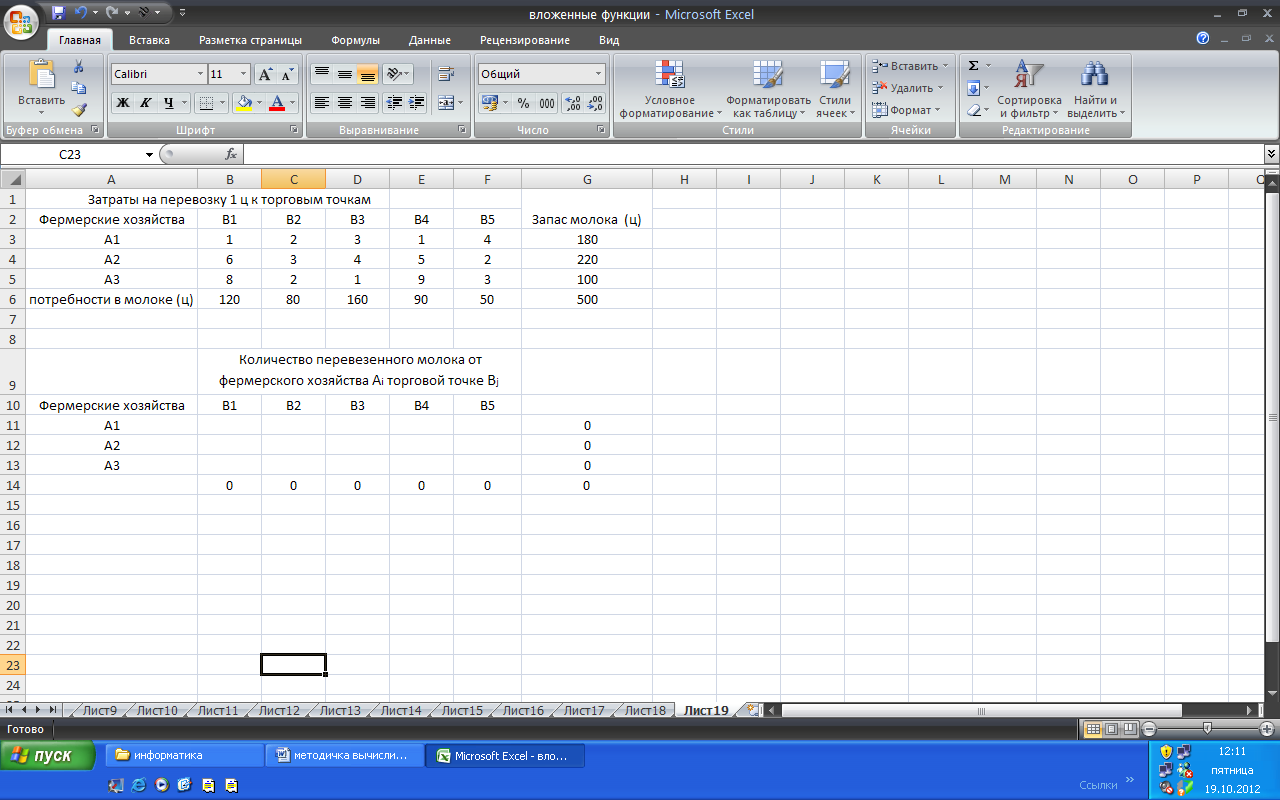
Рис. 1.15. Создана форма для решения задачи, введена зависимость для целевой функции

На рис. 1.16 отражены введенные формулы.

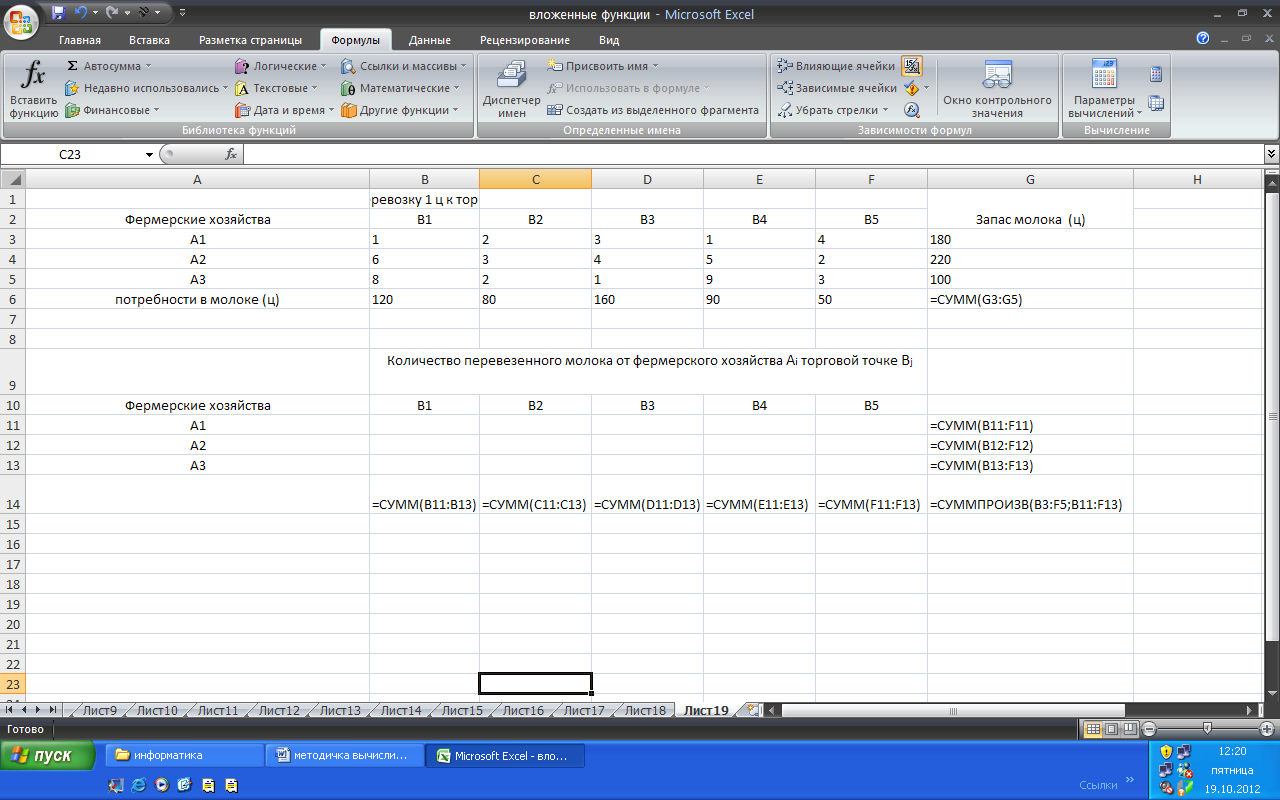
Рис. 1.16. Вид введенных формул

5. Запускаем команду Поиск решений.

6. Назначаем ячейку для целевой функции.

Поместим курсор в окно Установить целевую ячейку.

Введем адрес ячейки $G$14 (рис. 1.17).

Введем тип целевой функции. Для этого отметим, чему равна целевая функция — Минимальному значению.

7.Вводим ограничения.

· Помещаем указатель мыши на кнопку Добавить. Появится диалоговое окно добавление ограничения.

Первая запись в группе Ограничения (см. рис. 1.17) пред­ставляет собой фиксированную перевозку, вторая запись - ограничения по уровню спроса, третья и четвертая запись- запрет на перевозки, пятая запись — ограничения по уровню запасов.

· После ввода всех ограничений нажимаем кнопку ОК.

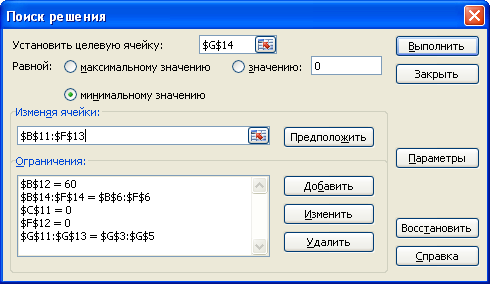
Рис. 1.17. Введены все условия задачи