Многомерная центральная предельная теорема.
Пусть 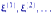 — последовательность независимых и одинаково распределенных случайных векторов, каждый из которых имеет среднее
— последовательность независимых и одинаково распределенных случайных векторов, каждый из которых имеет среднее  и невырожденную матрицу ковариаций
и невырожденную матрицу ковариаций 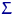 . Обозначим через
. Обозначим через 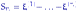 вектор частичных сумм.
вектор частичных сумм.
Тогда при  имеет место слабая сходимость распределений векторов
имеет место слабая сходимость распределений векторов
 , где
, где 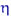 имеет распределение
имеет распределение  .В условиях многомерной ЦПТ распределение любых непрерывных функций
.В условиях многомерной ЦПТ распределение любых непрерывных функций 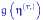 слабо сходится к распределению
слабо сходится к распределению  . В качестве
. В качестве 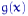 нам будет нужна только
нам будет нужна только  .
.
Следствие 5.
В условиях многомерной ЦПТ имеет место сходимость  .
.
42 корреляция
Среднеквадратичным отклонением (англ. standart deviation) 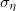 называется величина, равная квадратному корню из дисперсии случайной величины
называется величина, равная квадратному корню из дисперсии случайной величины 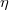
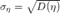
Пусть 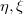 — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда корреляцией случайных величин(англ. correlation)
— две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда корреляцией случайных величин(англ. correlation) 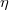 и
и 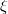 называется выражение следующего вида:
называется выражение следующего вида:
 , где
, где 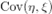 — ковариация случайных величин.
— ковариация случайных величин.
Заметим, что 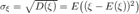 — среднеквадратичное отклонение.
— среднеквадратичное отклонение.
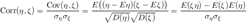
Значительная корреляция между случайными величинами всегда означает, что присутствует некая взаимосвязь между значениями конкретной выборки, но при другой выборке связь вполне может отсутствовать. Поэтому при нахождении взаимосвязи не нужно делать поспешных выводов о причинно-следственном характере величин, а следует рассмотреть наиболее полную выборку, чтобы делать какие-либо выводы. Коэффициенты корреляции устанавливают лишь статистические взаимосвязи, но не более того.
Если  , то
, то 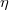 и
и 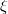 линейно зависимы.
линейно зависимы.
Если 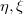 независимые случайные величины, то
независимые случайные величины, то 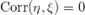 .
.
Пусть 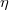 и и 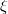 — независимые величины. Тогда — независимые величины. Тогда 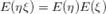 , где , где 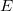 — их математическое ожидание. Получаем: — их математическое ожидание. Получаем: 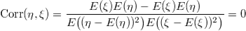 Но обратное неверно: Пусть Но обратное неверно: Пусть 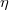 — случайная величина, распределенная симметрично около — случайная величина, распределенная симметрично около 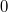 , а , а  . . 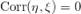 , но , но 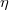 и и 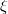 — зависимые величины. — зависимые величины. |
43. 
44. Генеральная и выборочная совокупности
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.
Иногда проводят сплошное обследование, то есть обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Различают генеральную и выборочную совокупности:
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности 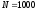 , а объем выборки
, а объем выборки 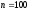 .[1]
.[1]
Замечание. Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения вычислений, или для облегчения теоретических выводом, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. [3]
