Структурный анализ, аналог скорости, приведенный момент, работа сил, кинетическая энергия, маховик, ускорение, зубчатая передача

Записка, 56 с. Ил. 6.Табл.: 13. Библиогр.: 9 назв.

Объект исследования - механизм двигателя внутреннего сгорания, его зубчатая передача.

Цель работы - динамический синтез и анализ механизма двигателя внутреннего сгорания.

В курсовой работе выполнены: геометрический синтез рычажного механизма по заданному коэффициенту изменения средней скорости ползуна; динамический синтез и анализ рычажного механизма, в результате которого определен необходимый момент инерции маховика для заданного коэффициента неравномерности хода, основные кинематические характеристики механизма, реакции в кинематических парах и внешняя сила, приложенная к начальному звену; синтез зубчатой передачи.

Геометрический синтез рычажного механизма выполнен аналитически, динамический синтез - графоаналитическим методом, динамический анализ -методом кинетостатики и по методу " жесткого " рычага Жуковского. Расчеты для синтеза зубчатой передачи произведены на ПК.

Геометрический синтез механизма двигателя

Провести синтез механизма двигателя, структурный анализ которого рассмотрен в разделе 1 (рис. 1.1).

Входные данные: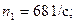

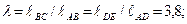
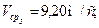
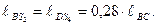
Допустим, что кривошип вращается равномерно. Вычислим его угловую скорость:

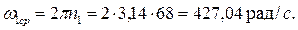
В случае, если частота вращения n₁ начального звена указывается с единицей физической величины 1/c, то вычисление угловой скорости следует вести по формуле:

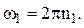
Определим время одного оборота кривошипа:

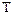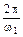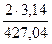= = = 0,0147 c.

Для вычисления хода поршней используем зависимость:

2 =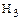

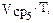
откуда:

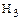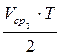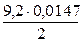= = = 0,0676 м;

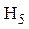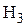= = 0,0676 м.

Рассмотрим механизм в крайних положениях, найдем длины кривошипов 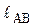и :

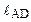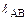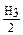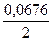= = = 0,0338 м;

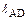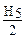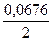= = = 0,0338 м.

Длины шатунов определим, используя заданный коэффициент :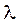

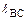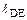= = 3,8∙ 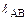= 3,8 ∙ 0,0338 = 0,12844 м.

Положение центров масс шатунов определяются расстоянием:

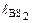= 0,28∙ 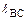= 0,28 0,12844 = 0,036 м.

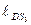= 0,28∙ 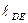= 0,28 0,12844 = 0,036 м.

3. Динамический синтез механизма двигателя

Цель работы: определить положения, траектории, скорости и ускорение точек и звеньев механизма с заданной угловой скоростью и направлением обращения начального звена [1;4].

Примем: длины звеньев - неизменные; зазоры в кинематических парах - отсутствуют.

Динамический анализ механизма

Определение закона движения начального звена

Для определения угловой скорости начального звена воспользуемся кривой 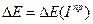и формулой:

,

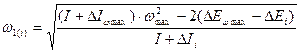где: I = 0,1949 кг*м² – момент инерции на начальном звене;

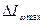- момент инерции в точке, в которой угловая скорость максимальна;

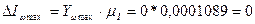кг*м².

.

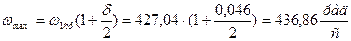Определим постоянные величины.

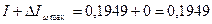кг*м²

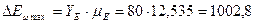Дж.

Определим угловую скорость для положения 1’

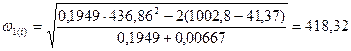рад/с.

Значения угловой скорости представлены в таблице 4.1.

Угловое ускорение начального звена определяется по формуле:

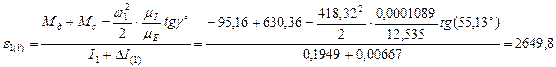рад/с².

Проверим 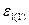по формуле:

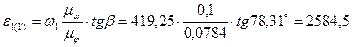рад/с².

СИНТЕЗ ЗУБЧАТОЙ ПЕРЕДАЧИ

Цель синтеза: выполнить геометрический расчет прямозубой эвольвентной цилиндрической зубчатой передачи, колеса которой нарезаны без подрезания; определить качественные показатели зубчатой передачи.

Записка, 56 с. Ил. 6.Табл.: 13. Библиогр.: 9 назв.

Объект исследования - механизм двигателя внутреннего сгорания, его зубчатая передача.

Цель работы - динамический синтез и анализ механизма двигателя внутреннего сгорания.

В курсовой работе выполнены: геометрический синтез рычажного механизма по заданному коэффициенту изменения средней скорости ползуна; динамический синтез и анализ рычажного механизма, в результате которого определен необходимый момент инерции маховика для заданного коэффициента неравномерности хода, основные кинематические характеристики механизма, реакции в кинематических парах и внешняя сила, приложенная к начальному звену; синтез зубчатой передачи.

Геометрический синтез рычажного механизма выполнен аналитически, динамический синтез - графоаналитическим методом, динамический анализ -методом кинетостатики и по методу " жесткого " рычага Жуковского. Расчеты для синтеза зубчатой передачи произведены на ПК.

Структурный анализ, аналог скорости, приведенный момент, работа сил, кинетическая энергия, маховик, ускорение, зубчатая передача

ВВЕДЕНИЕ

Объектом исследования является четырехтактный двухцилиндровый двигатель внутреннего сгорания.

Двигатель включает в себя различные механизмы, из которых исследованию подлежат - рычажный, зубчатый и кулачковый.

Рычажный механизм служит для преобразования возвратно-поступательное перемещение поршня во вращательное движение кривошипа.

От кривошипа вращательное движение передается через зубчатую передачу. В рычажных механизмах угловая скорость непостоянна и для более равномерного движения на валу кривошипа установлен маховик.

Для управления зажимом деталей применяется кулачковый механизм, который служит для преобразования вращательного движения в поступательное движение ведомого звена.

1. Структурный анализ механизма

Цель анализа: изучение строения кинематической цепи; определение степени движимости; выяснение, удовлетворяет ли заданная кинематическая цепь понятию “механизм”; последовательности отделения структурных групп, их класса, порядка и вида; класса механизма [1;2].

Заданная кинематическая цепь состоит из звеньев: 0 - стойка, 1 - кривошип, 2 - шатун, 3 - ползун, 4 - шатун, 5 - ползун. Звенья соединены кинематическими парами, характеристика которых представлена в табл. 1.1.

Вычислим степень движимости кинематической цепи по формуле Чебышева: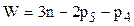

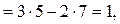
где 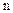=5 - число подвижных звеньев;

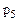=7 - число кинематических пар пятого класса; 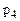=0 - число кинематических пар четвертого класса.

Таблица 1.1

Характеристика кинематических пар

	Характеристика кинематических пар
Обозначение Кинематической пары	А	В	D	C	C’	E	E'
Звенья, которые образовывают кинематические пары	0,1	1,2	1,4	2,3	3,0	4,5	5,0
Вид допускаемого относительного движения	Вращат.	Вращат.	Вращат.	Вращат.	Пост.	Вращат.	Пост.
Класс кинематической пары

Степень подвижности совпадает с числом начальных звеньев. Таким образом, заданная кинематическая цепь является механизмом.

Выделим структурные группы (рис. 1.2, 1.3):

Часть оставшейся кинематической цепи является группой начальных звеньев (рис.1.4):

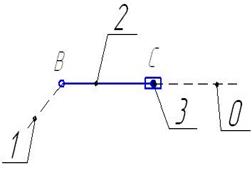
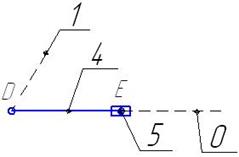
Рис. 1.1. Рис. 1.2.

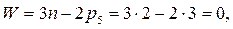
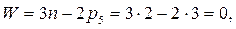
2-й класс, 2-й класс,

2-й порядок, 2-й порядок,

2-й вид; 2-й вид.

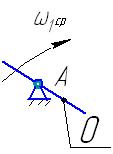
Рис.1.3.

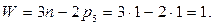
Заданный механизм является механизмом 2-го класса, так как структурные группы выше 2-го класса отсутствуют.