Измерение вертикальных углов

Вертикальный угол - это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние. Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν. Углы наклона бывают положительные и отрицательные.

Угол между вертикальным направлением и направлением линии местности называется зенитным расстоянием и обозначается буквой Z. Зенитные расстояния всегда положительные (рис.4.20).

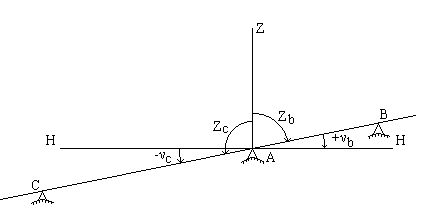
Рис.4.20

Угол наклона и зенитное расстояние одного направления связаны соотношением:

Z + ν = 90o , (4.22)

или

ν = 90o - Z , (4.23)

или

Z = 90o - ν . (4.24)

Вертикальный круг теодолита. Вертикальный круг теодолита предназначен для измерения вертикальных углов, то-есть, углов наклона или зенитных расстояний.

Вертикальный круг большинства теодолитов устроен следующим образом: лимб вертикального круга жестко соединен с трубой (насажен на один из концов оси трубы), центр лимба совмещен с геометрической осью вращения трубы, а его плоскость перпендикулярна этой оси. Деления на лимбе наносят по разному: либо от 0o до 360o, либо от 0o до 180o в обе стороны со знаками "плюс" и "минус" или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.

Пузырек уровня в момент отсчета приводится в нуль-пункт, то есть, ось уровня служит указателем горизонтального направления. Отсчетным индексом является нулевой штрих отсчетного приспособления. Ось уровня и линия отсчетного индекса (линия, соединяющая отсчетный индекс с центром лимба) должны быть параллельны; при выполнении этого условия линия отсчетного индекса будет горизонтальна в момент взятия отсчета по вертикальному кругу.

Взаимное положение лимба и зрительной трубы должно удовлетворять условию: визирная линия трубы и нулевой диаметр лимба должны быть параллельны.

Оба условия вместе составляют так называемое главное условие вертикального круга теодолита; оно читается так: визирная линия трубы должна занимать горизонтальное положение, когда отсчет по лимбу равен нулю и пузырек уровня находится в нульпункте. На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис.4.21-а.

Во-первых, при насаживании лимба на ось трубы между нулевым диаметром лимба и визирной линией трубы остается малый угол x. Во-вторых, линия отсчетного индекса может быть непараллельна оси уровня и между ними существует малый угол y. Таким образом, хотя отсчет по лимбу равен нулю, визирная линия трубы занимает наклонное положение, и угол наклона ее равен:

ν = x + y.

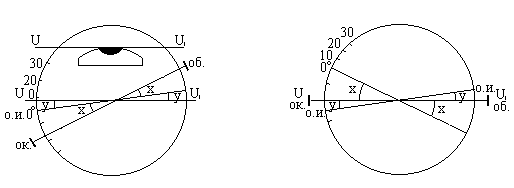
Рис.4.21

Если установить визирную линию горизонтально (рис.4.21-б), то отсчет по лимбу станет равным:

N = 360o - (x + y). (4.25)

Этот отсчет называется местом нуля вертикального круга и обозначается М0.

Таким образом, место нуля вертикального круга теодолита - это отсчет по лимбу вертикального круга при горизонтальном положении визирной линии трубы и оси уровня вертикального круга.

Для конкретного теодолита формулы для вычисления угла наклона и места нуля приводятся в паспорте. Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:

М0 = 0.5 . (NL + NR), (4.26)

ν = 0.5 . (NL - NR),

ν = NL - M0,

ν = M0 - NR.

Положение вертикального круга, при котором отсчет по лимбу вертикального круга равен (с точностью до M0) углу наклона, считается основным; у большинства современных теодолитов основным положением является КЛ.

Для измерения углов наклона удобно иметь М0 близким к нулю, поэтому нужно регулярно выполнять поверку места нуля, которая предусматривает следующие действия:

наведение трубы на точку при КЛ, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,

перевод трубы через зенит, наведение трубы на точку при КП, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,

вычисление по соответствующим формулам места нуля М0 и угла наклона ν.

Если М0 получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нульпункта. Исправительными винтами уровня привести пузырек в нульпункт.

Измерение расстояний

Мерные приборы

Различают непосредственное измерение расстояний и измерение расстояний с помощью специальных приборов, называемых дальномерами. Непосредственное измерение выполняют инварными проволоками, мерными лентами и рулетками.

Инварные проволоки позволяют измерять расстояние с наибольшей точностью; относительная ошибка измерения может достигать одной миллионной; это означает, что расстояние в 1 км измерено с ошибкой всего 1 мм. Инвар - это сплав, содержащий 64% железа и 36% никеля; он отличается малым коэффицентом линейного расширения α = 0.5 * 10-6 (для сравнения: сталь имеет α = 12 * 10-6).

Мерные ленты обеспечивают точность измерений около 1 / 2 000, т.е. для расстояния в 1 км ошибка может достигать 50 см. Мерная лента - это стальная лента шириной от 10 до 20 мм и толщиной 0.4 - 0.5 мм (рис.4.22). Мерные ленты имеют длину 20, 24 и 50 м. Целые метры отмечены пластинами с выбитыми на них номерами метров, полуметры отмечены круглыми заклепками, дециметры - круглыми отверстиями диаметром 2 мм.

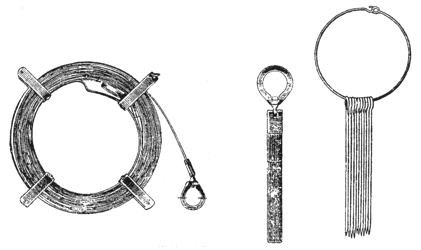
Рис.4.22

Фактическая длина ленты или проволоки обычно отличается от ее номинальной длины на величину Δl. Фактическую длину ленты определяют, сравнивая ее с эталонной мерой. Процесс сравнения длины мерного прибора с эталоном называется компарированием, а установка, на которой производится компарирование, - компаратором.

Согласно ГОСТ 7502 - 80 допускается отклонение фактической длины новой ленты 2 мм для 20- и 30-метровых лент и 3 мм для 50-метровых. Вследствие износа фактическая длина ленты изменяется, поэтому компарирование производится каждый раз перед началом полевых работ.

Длина стальных рулеток бывает 20, 30, 50, 75 и 100 м. Точность измерения расстояния стальными рулетками зависит от методики измерений и колеблется от 1/2 000 до 1/10 000.

Измерение линий мерной лентой. Измеряют линии, последовательно укладывая мерную ленту в створе линии. Прежде чем измерять линию, ее нужно подготовить, а именно: закрепить на местности ее концевые точки и обозначить створ. Створом линии называют отвесную плоскость, проходящую через концевые точки. Для обозначения створа линию провешивают, т.е. устанавливают вехи через 50-150 м в зависимости от рельефа.

Измерение линии выполняют два человека. Они укладывают ленту в створ и считают число уложений. В комплект кроме самой ленты входят 6 или 11 шпилек и 2 проволочных кольца (рис.4.1), на которые надевают шпильки. Передний мерщик в процессе измерения линии втыкает шпильки в землю, а задний собирает их. В конце линии измеряют остаток с точностью до 1 см.

Длину линии определяют по формулам:

D'= k * ( l0 + Δl) + r + (Δl/l0) * r, (4.27)

D = D'+ D'* a * (t - tk) = D' * [1 + a * (t - tk)];

здесь l0- номинальная длина ленты;
Δl - поправка из компарирования;
k - число уложений ленты;
r - остаток;
tk - температура компарирования;
t - температура ленты во время работы.

Длину линии обычно измеряют два раза - в прямом и обратном направлениях. Допускается расхождение между результатами двух измерений на величину:

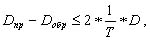
где 1/T - относительная ошибка измерения расстояния.

Например, при 1/T = 1/2000 и длине линии 500 м расхождение между прямым и обратным измерениями не должно превышать 0.5 м.

Приведение длины линии к горизонту. Измеренная линия имеет угол наклона ν ; проекция ее на горизонтальную плоскость, называемая горизонтальным проложением линии, вычисляется по формуле:

S = D - ΔD,

где ΔD- поправка за приведение к горизонту. Формула для вычисления поправки ΔD выводится следующим образом. Из ΔABB' (рис.4.23) видно, что:

S = D * Cos ν;

далее пишем:

ΔD = D - D * Cos ν = D * (1 - Cosν),

ΔD = 2 * D * Sin2 ν/2. (4.29)

Угол наклона линии измеряют либо теодолитом, либо специальным прибором - эклиметром. В исправном эклиметре нулевой диаметр всегда занимает горизонтальное положение. При наклоне эклиметра в прорезь виден отсчет, равный углу наклона линии. Ошибка измерения угла наклона эклиметром равна 15'- 30'.

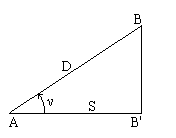
Рис.4.23

Если линия имеет переменный угол наклона, то ее нужно разделить на части, каждая из которых имеет постоянный угол наклона, и измерить каждую часть отдельно.

Если ν<10, то поправку за приведение к горизонту учитывать не нужно. Покажем это:

ΔD/D =2 * Sin2(ν/2); Sin(ν/2) = Sin30'= 1/115;

ΔD/D = 1/6500.

При ν=10 поправка за наклон не превышает 1/6500, а точность измерений мерной лентой - около 1/2000, следовательно, поправкой за наклон можно пренебречь.

Поправку ΔD за наклон линии можно вычислять и через превышение h точки B над точкой A. Запишем теорему Пифагора для треугольника ABB':

D2 = S2 + h2,

и выразим S

S = D * (1 - h2/D2)1/2.

Для выражения в скобках выполним разложение в ряд, ограничившись двумя членами разложения,

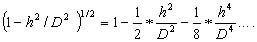
Тогда

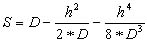
и

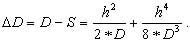
При измерении расстояний мерными лентами и рулетками второе слагаемое иногда не учитывают и применяют формулу:

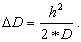(4.30)

Оптические дальномеры

В дальномерах измеряется не сама длина линии, а некоторая другая величина, относительно которой длина линии является функцией.

В геодезии применяют 3 вида дальномеров:

оптические (дальномеры геометрического типа),

электрооптические (светодальномеры),

радиотехнические (радиодальномеры).

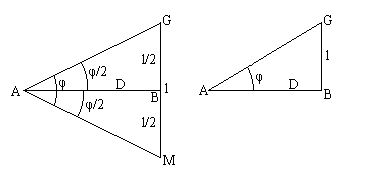
Рис.4.24

Геометрическая схема оптических дальномеров. Пусть требуется найти расстояние АВ. Поместим в точку А оптический дальномер, а в точку В перпендикулярно линии АВ - рейку.

Обозначим: l - отрезок рейки GM,
φ - угол, под которым этот отрезок виден из точки А.

Из треугольника АGВ имеем:

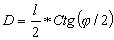(4.31)

или

D = l * Ctg(φ). (4.32)

Обычно угол φ небольшой (до 1o) , и, применяя разложение функции Ctgφ в ряд, можно привести формулу (4.31) к виду (4.32). В правой части этих формул два аргумента, относительно которых расстояние D является функцией. Если один из аргументов имеет постоянное значение, то для нахождения расстояния D достаточно измерить только одну величину. В зависимости от того, какая величина - φ или l, - принята постоянной, различают дальномеры с постоянным углом и дальномеры с постоянным базисом.

В дальномере с постоянным углом измеряют отрезок l, а угол φ - постоянный; он называется диастимометрическим углом.

В дальномерах с постоянным базисом измеряют угол φ, который называется параллактическим углом; отрезок l имеет постоянную известную длину и называется базисом.

Нитяной дальномер с постоянным углом. В сетке нитей зрительных труб, как правило, имеются две дополнительные горизонтальные нити, расположенные по обе стороны от центра сетки нитей на равных расстояниях от него; это - дальномерные нити (рис.4.25).

Нарисуем ход лучей, проходящих через дальномерные нити в трубе Кеплера с внешней фокусировкой. Прибор установлен над точкой А; в точке В находится рейка, установленная перпендикулярно визирной линии трубы. Требуется найти расстояние между точками А и В.

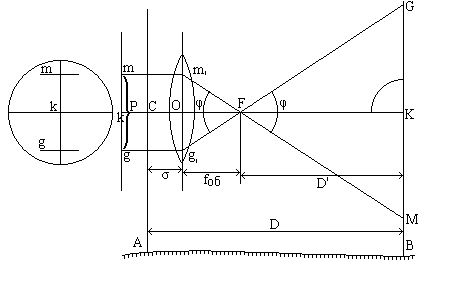
Рис.4.25

Построим ход лучей из точек m и g дальномерных нитей. Лучи из точек m и g, идущие параллельно оптической оси, после преломления на линзе объектива пересекут эту ось в точке переднего фокуса F и попадут в точки М и G рейки. Расстояние от точки A до точки B будет равно:

D = l/2 * Ctg(φ/2) + fоб + d, (4.33)

где d - расстояние от центра объектива до оси вращения теодолита;
fоб-фокусное расстояние объектива;
l - длина отрезка MG на рейке.

Обозначим (fоб + d) через c, а величину 1/2*Ctg φ/2 - через С, тогда

D = C * l + c. (4.34)

Постоянная С называется коэффицентом дальномера. Из Dm'OF имеем:

Ctg φ/2 = ОF/m'O; m'O= p/2; Ctg φ/2 = (fоб*2)/p,

где p - расстояние между дальномерными нитями. Далее пишем:

С = fоб/p. (4.35)

Коэффициент дальномера равен отношению фокусного расстояния объектива к расстоянию между дальномерными нитями. Обычно коэффицент С принимают равным 100, тогда Ctg φ/2 = 200 и φ = 34.38'. При С = 100 и fоб = 200 мм расстояние между нитями равно 2 мм .

Измерение нитяным дальномером наклонного расстояния. Пусть визирная линия трубы JK при измерении расстояния АВ имеет угол наклона ν, и по рейке измерен отрезок l (рис.4.26). Если бы рейка была установлена перпендикулярно визирной линии трубы, то наклонное расстояние было бы равно:

D = l0 * C + c.

Но l0 = l*Cos ν, поэтому

D = C*l*Cosν + c. (4.36)

Горизонтальное проложение линии S определим из Δ JKE :

S = D*Cosν или

S= C*l*Cos2ν + c*Cosν. (4.37)

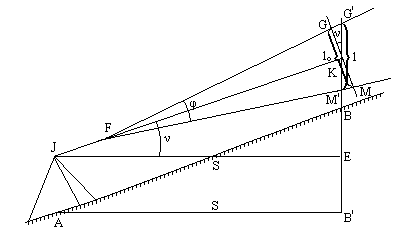
Рис.4.26

Для удобства вычислений принимаем второе слагаемое равным с*Cos2ν ; поскольку с величина небольшая (около 30 см), то такая замена не внесет заметной ошибки в вычисления. Tогда

S = (C * l + c) * Cos2ν, или

S = D'* Cos2ν. (4.38)

Oбычно величину (C*l + c) назыывают дальномерным расстоянием. Обозначим разность (D' - S) через ΔD и назовем ее поправкой за приведение к горизонту, тогда

S = D' - ΔD,

где ΔD = D' * Sin2 ν. (4.39)

Угол ν измеряют вертикальным кругом теодолита; причем при 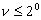поправка ΔD не учитывается. Точность измерения расстояний нитяным дальномером обычно оценивается относительной ошибкой от 1/100 до 1/300.

Кроме обычного нитяного дальномера существуют оптические дальномеры двойного изображения.

Понятие о светодальномерах

Измерение расстояний с помощью светодальномера основано на измерении промежутка времени t, в течение которого свет дважды проходит расстояние D, в прямом и обратном направлении (рис.4.27).

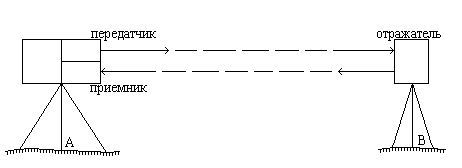
Рис.4.27

Обозначив через V скорость света в атмосфере, напишем формулу для расстояния:

D = V * t/2. (4.40)

Скорость света в вакууме V0 считается известной V0 = 299 792 458 м/сек, а для получения скорости света в атмосфере V нужно еще знать показатель преломления воздуха n:

V = V0/n . (4.41)

Светодальномеры бывают импульсные и фазовые. В импульсных светодальномерах промежуток времени t измеряется непосредственно,а в фазовых - через разность фаз.

В фазовых светодальномерах используют модулированный свет; частота модуляции бывает от 7 мгц до 75 мгц (что соответствует длине волны от 4 до 40 метров); это так называемая измерительная или масштабная частота; несущие волны располагаются в субмиллиметровом диапазоне.

Приведем рабочие формулы для вычисления расстояний, измеренных фазовым светодальномером:

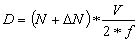
или D = (N + ΔN) * λ/2 . (4.42)
где: f - масштабная частота,
l - длина волны, соответствующая масштабной частоте,
N - число, показывающее сколько раз половина длины волны укладывается в измеряемом расстоянии; оно определяется при "грубом" измерении расстояния на нескольких масштабных частотах, ΔN - домер фазового цикла; именно он и подлежит точному измерению.

На практике для вычисления горизонтального проложения линии, измеренной светодальномером, используют формулу:

Sизм = Dст. + ΔD t + ΔDP + ΔDe + C - ΔDH , (4.43)

где: Dст.- длина линии, соответствующая некоторому стандартному значению скорости света Vст. при значениях температуры t0 и давления P0; обычно принимают:

t0 = + 12oC, P0 = 984 ГПА ,

ΔDt, ΔDP, ΔDe - поправки за отклонение фактических значений метеоэлементов от их стандартных значений,

ΔDt = kt * Dст./100, ΔD P = kP * Dст./100, ΔDe = ke * Dст./100.

Коэффициенты kt (температурный), kP (давления) и ke (влажности воздуха) выбирают из заранее составленной таблицы,
C- постоянная поправка светодальномера, определяемая по специальной методике,
ΔDH - поправка за наклон линии:

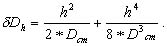(4.44)

Согласно ГОСТу 19223-90 светодальномеры в нашей стране выпускаются четырех типов (групп):
Г - для государственных геодезических сетей;
П - для прикладной геодезии и маркшейдерии;
Т - для сетей сгущения и топографических съемок;
СТД - для топографических съемок (диффузное отражение).

Средняя квадратическая ошибка расстояния, измеренного светодальномером, вычисляется по формуле:

mD = a + b * D * 10-6.

Для каждой группы светдальномеров значения коэффициентов a и b имеют значения:
СГ (0.1 км < D < 30 км) a = 1мм; 2 мм; b = 1; 2;
СП (0.001 км < D < 5 км) a = 0.1мм; 0.5 мм; 1мм; 2 мм;
СТ (0.002 км < D < 15 км) a = 5 мм; 10мм; b = 3; 5;
СТД (0.002 км < D < 500 м) a = 20 мм.

Устройство конкретного светодальномера, порядок его поверок и исследований, правила подготовки к работе, методика измерения расстояния, обработка измерений, - все это подробно описывается в документации, прилагаемой к каждому экземпляру светодальномера.

Приведение измеренного расстояния к центрам пунктов. При измерении расстояния светодальномером может возникнуть ситуация, когда центрирование светодальномера и отражателя выполнить не удается; в этом случае нужно ввести в измеренное расстояние поправки за центрировку и редукцию.

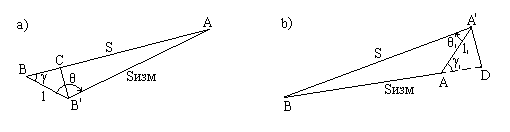
Рис.4.28

Пусть на рис.4.28-а точка B обозначает центр пункта, а точка B' - проекцию на горизонтальную плоскость оси вращения светодальномера; точка A обозначает центр второго пункта. Измерим элементы центрировки: l - линейный элемент и Θ - угловой элемент; по аналогии с центрировкой теодолита (раздел 4.1.4) угол Θ строится при проекции оси вращения прибора и отсчитывается от линейного элемента по ходу часовой стрелки до направления на наблюдаемый пункт A.

В треугольнике BAB' угол при точке A очень мал, поэтому в зависимости от положения точки B' относительно точки B будет выполняться одно из равенств:

γ = Θ, γ = 180o - Θ, γ = Θ - 180o, γ = 360o - Θ. (4.45)

Опустим перпендикуляр из точки B' на линию BA, тогда поправка за центрировку будет равна:

ΔSc = BC = 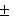l * Cos(g) = - l * Cos(Θ). (4.46)

Аналогичные построения на пункте установки отражателя (A - центр пункта, A' - проекция оси вращения отражателя, l1 - линейный элемент и Θ1 - угловой элемент редукции) позволяют написать формулу:

ΔSо = AD = 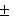l1 * Cos(g1) = - l1 * Cos (Θ1). (4.47)

Расстояние S, приведенное к центрам пунктов будет равно:

S = Sизм + Δ Sс + ΔSо. (4.48)

Измерение превышений