Фреймовые модели представления знаний

Модели представления знаний

На рис. 2.10 приведена классификация моделей представления знаний.

В процедурных моделях логическая модель реализует как объекты, так и правила с помощью предикатов первого порядка, является строго формализованной, использующей с универсальный дедуктивный и монотонный метод логического вывода «от цели к данным».

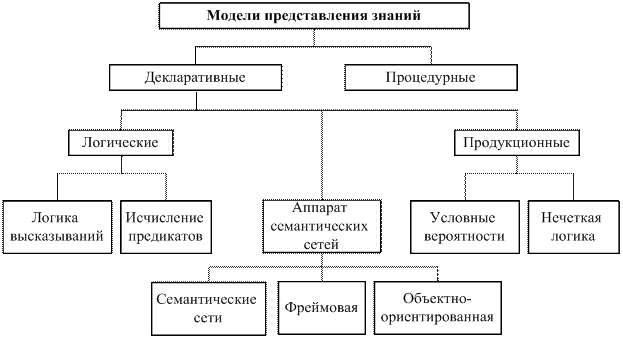
Рис. 2.10. Классификация моделей представления знаний

Под предикатом понимается логическая функция на N – аргументах (признаках), которая принимает истинное или ложное значение в зависимости от значений этих аргументов.

Продукционные модели используются для решения более сложных задач, которые основаны на применении эвристических методов представления знаний, позволяющих настраивать механизм вывода на особенности ПрО и учитывать неопределенность знаний.

В такой модели основной единицей знаний служит правило в виде

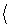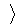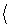«если «посылка» , то «заключение» »,

с помощью которого могут быть выражены пространственно-временные, причинно-следственные, функционально-поведенческие (ситуация – действие) отношения объектов. Эта модель предназначена, главным образом, для описания последовательности различных ситуаций или действий и в меньшей степени для структурированного описания объектов.

Для логической модели характерна строгость формального аппарата получения решения. Однако полный последовательный перебор всех возможных решений может приводить к комбинаторным взрывам, в результате чего решение поставленных задач может занимать недопустимо много времени. Работа с неопределенностями знаний должна быть запрограммирована в виде самостоятельных метаправил, что на практике затрудняет разработку БЗ с помощью логического формализма.

Семантическая сеть отображает разнообразные отношения объектов.

Фреймовая модель как частный случай семантической сети использует для реализации операционного знания присоединенные процедуры.

Объектно-ориентированная модель как развитие фреймовой модели, реализуя обмен сообщениями между объектами, в большей степени ориентирована на решение динамических задач и отражение поведенческой модели.

Для обработки неопределенностей знаний продукционная модель использует, как правило, либо методы обработки условных вероятностей (байесовский подход), либо методы нечеткой логики.Такой подход предполагает начальное априорное задание некоторых гипотез (значений достигаемых целей), которые последовательно уточняются. С учетом вероятностей формируются апостериорные вероятности.

Для байесовского подхода к построению продукционной БЗ характерна большая трудоемкость статистического оценивания априорных шансов и факторов достаточности и необходимости.

Логические модели

Одним из методов представления знаний является логический метод, в основе которого лежит логика пре­дикатов [28]. Удобство его использования заключается в том, что свойственный ему механизм вывода, во-первых, допускает высокую степень формализации и обладает привычными математическими свойст­вами, и, во-вторых, может быть непосредственно за­программирован.

Одним из центральных вопросов логики предикатов является вопрос о том, можно ли из не­скольких исходных логических формул получить конеч­ную. Например, можно ли из каких-либо предпосылок вычислить заключение.

Логика предикатов является обобщением и рас­ширением логики высказываний, а высказывание яв­ляется центральной категорией логики предикатов.

Высказыванием называют предложение, которое мо­жет принимать одно из двух значений: истина или ложь.

Логика предикатов имеет свои синтаксис и алфа­вит. Алфавит обычно состоит из символов шести типов, обозначаемых буквами без индексов или теми же буквами с индексами:

1. Переменные: х, у, z, и 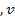, w.

2. Константы: а, b, с, d, e .

3. Функциональные символы: f, g, h .

4. Предикативные символы: р, r, s, t .

5. Логические символы:Ù, Ú, Ø, É, $, ";

6. Вспомогательные символы: запятые, скобки, иначе символы, не входя­щие в первые пять групп.

Предикативные символы служат для описания свойств объектов предметной области и отношений между ними.

При построении ИОС строится последовательность проведения работ по преобразованию предметно-ориентированного языка в язык предикатов, т. е. демонстрируется сведение контекстно-зависимого (естественного языка человека) предметно-ориентированного языка к машинно-представимому, что является основой для построения ОС, в которых реализуется возможность интеллектуального управления процессом обучения.

Продукционные модели

Продукционный метод является наиболее рас­пространенной моделью представления знаний в экс­пертных системах [14, 28 ]. В его основе лежат так называемые продукционные правила, или продукции, которые с помощью импликации связывают факты: «если A, то B». Правила устанавливают связь между фактами (знаниями вида «A это A»), содержащимися в условной части (А), и фактами, находящимися в заключительной его части (В).

Часто конкретные факты описывают состояния (человек или искусственная система формирования понятий). Объекты можно различать по тем значениям, которые имеют характеризующие их признаки, или атрибуты, т. е. те неотъемлемые свойства объекта (предмета), без которого тот не может существовать.

Применительно к воздушной навигации определение траектории звучит следующим образом: «траектория полета – пространственная линия, описываемая центром масс летательного аппарата при движении».

Системы, основанные на продукционном методе пред­ставления знаний, называют продукционными (рис. 2.11).

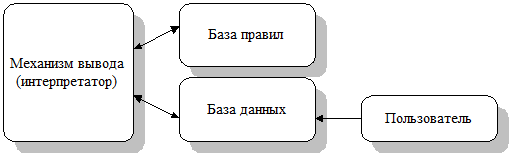
Рис.2.11. Фрагмент продукционной системы

Эти системы включают в себя три обязательных компонента: базу правил, базу данных, или рабочую память, и интерпретатор, или механизм вывода.

База правил (БП) является частью базы знаний и состоит из набора продукций (правил вывода). База данных (БД) содержит множество фактов, описывающих исходную ситуацию, заданную пользователем системы, а также факты, выведенные из исходных при срабатывании правил, т. е. являющиеся заключением этих правил. Механизм вывода осуществляет просмотр фактов в базе данных и сопоставление их с фактами из условной части правил, находящихся в базе правил, а также определяет порядок просмотра этих правил. Если при просмотре какого-либо правила окажется, что все факты из его условной части имеются и в базе данных, то условная часть правила считается истинной, в противном случае она считается ложной. Так просматриваются все правила и факты.

Семантические сети и графы

Важным шагом на пути выявления структуры, при­сущей знаниям, является построение моделей, в которых в явной форме выделены объекты, образующие её структуру [14, 28]. В основе таких моделей лежит понятие сети, состо­ящей из вершин, или узлов, соединенных дугами. С вершинами этой сети сопоставляются понятия (объекты, события, процессы, явления и др.), а с дуга­ми – связи, или отношения, существующие между этими понятиями.

Графическое изображение элемен­тов сети произвольное. Объекты могут изображаться точками, кружками, прямоугольниками и другим образом, дуги могут быть прямыми, ломаными, кривы­ми линиями.

Семантические сети (СС), с одной стороны, имитируют понимание естественного языка человеком, а с другой, придают фактическим знаниям графовую структурированную организацию, они представляют собой так называемые ориентиро­ванные графы [14]. Построение СС как графа помогает осмыслению знаний, способствует их конкре­тизации, выявлению противоречий, обнаружению не­достающей информации и т. п.

В качестве понятий СС обычно выступают абстрактные или конкретные объекты. Тип отношений может быть самым разным, что позволяет в достаточной мере обеспечить в них такой признак знаний, как связность. В общем случае это означает, что в виде СС можно отобразить знания, заключенные в текстах на естественном языке.

В этом примере передаются отноше­ния «абстрактное» – «конкретное» и свойства объектов, их функциональные связи.

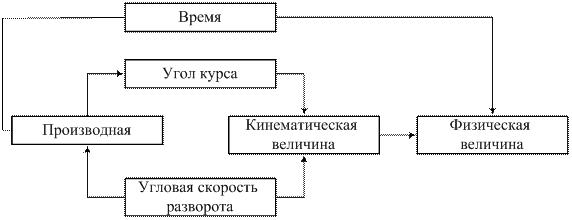
Рис. 2.12. Представление определения угловой скорости разворота с помощью семантической сети

Семантические отношения могут быть условно разделены на четыре класса: лингвистические, логические, теоретико-множественные и квантификационные.

В общем случае СС должна обес­печивать:

– хранение сведений о понятиях и связях между ними;

– возможность поиска понятий по заданным характеристикам (связям с другими понятиями);

– возможность пополнения и кор­ректировки знаний системы в процессе обучения (ввод новых понятий, установление новых связей, удаление существующих понятий и связей);

– возможность осуществления процедуры обобщения и конкретизации знаний; – отражение иерархичности предметных знаний;

– понятность для эксперта – специалиста в ПрО [14].

Измерительные шкалы

Тест - это объективное и стандартизированное измерение, легко поддающееся количественной оценке, статистической обработке и сравнительному анализу.

Измерение можно проводить на 4 уровнях. Каждому уровню соответствует своя шкала.

1. Номинальная шкала (наименовальная).
2. Порядковая шкала (ранговая).
3. Интервальная шкала.
4. Пропорциональная шкала.

Номинальная шкала

Самый низкий уровень измерения. Здесь устанавливается подобие или различие объектов относительно какого-либо признака, то есть устанавливается качественная однородность признака.
Проводится классификация по одной категории (например, по половому признаку: мужчина или женщина) или по нескольким признакам (например, учащиеся гимназии, простой городской школы, спецшколы; женат, разведен, холост, вдовец).

По результатам измерений можно подсчитать количество или частоты.

Величина основной тенденции (средняя величина) на номинальной шкале - есть модальная величина, то есть наиболее часто встречающаяся.

Считается, что такой тип измерений создает предпосылки для последующих более глубоких исследований. Данные шкалы используют в основном в социологических исследованиях.

Порядковая шкала

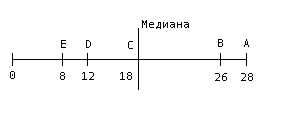
На данной шкале можно выделить лучших и худших.
Интервалы, разделяющие места в ряду не равны по величине, поэтому нецелесообразно и некорректно проводить математические действия с порядковыми местами, нельзя находить среднее арифметическое, т.е. нельзя сказать, насколько больше.

Можно определить медиану, как величину главной тенденции - это та величина, по обе стороны которой располагается равное количество многочисленных данных выборки.

Интервальная шкала

Позволяет ответить на вопрос, на сколько лучше (хуже), больше (меньше).
Здесь используются равные интервалы. Пример - градусник.

Для данной шкалы пропорции не устанавливают, а определяют:
1) точку отсчета;
2) направление отсчета;
3) величину единицы измерения.

Шкалы, используемые в тестировании - интервальные.
Хотя шкала интервала не позволяет нам сделать заключения о пропорциях между различными значениями шкалы, она тем не менее называется метрической и с ее помощью мы можем выполнять алгебраические действия (сложение и вычитание, вычисление среднего арифметического). То есть данная шкала имеет преимущества перед другими шкалами с точки зрения техники измерения.

Пропорциональная шкала

Позволяет сделать вывод о пропорциях, т.е. ответить на вопрос, во сколько раз. Потому что значению шкалы ноль соответствуют реальные значения признака (вес, длина). Данная шкала, как и номинальная в педагогике не используется, так как в педагогике нет абсолютного нуля. Чем ниже мы спускаемся по шкалам, тем сложнее математический аппарат для подсчета.

Нормированные шкалы

Рис. 1.Ц. Схема, иллюстрирующая возникновение и развитие ОС

различного типа:

1 — «Штатный» режим, 2 — Начальная стадия ОС, 3 — Развитие ОС, 4 — Заверше­ние полета; А — эксплуатационные ограничения, Б — I предельные ограничения, В — II предельные ограничения; а — усложнение .условий полета, б — сложная ситуация, в — аварийная ситуация, г — катастрофическая ситуация

Рассмотрим вначале методологию оценки критериев безопас­ности по материалам длительной эксплуатации воздушных судов, т. е. по статистическим данным, полученным из обработки резуль­татов реальных полетов и летных происшествий. В этом случае критерии определяются для некоего заданного календарного интер­вала времени Г_кал, например года или, в пределе, всего жизненного цикла рассматриваемого типа ЛА. Учитываются результаты эксплуа­тации определенного количества ЛА, а в предельном случае — всего располагаемого парка заданного типа.

Полная система оценок уровня безопасности, охватывающая вероятности возникновения всех четырех категорий ОС может относиться к осредненному полету или к осредненному часу поле­та за заданный календарный интервал.

В первом случае вероятность возникновения КС оценивается как

2.

вероятность возникновения АС

3.

вероятность возникновения СС

4.

вероятность возникновения ОС типа УУП

5.

6.

7.

Здесь N^*_п— полное количество полетов, выполненных за рассмат­риваемый интервал времени выбранным количеством (парком) ЛА;

N^*_КС— количество полетов, в которых возникли ОС, завер­шившиеся катастрофическим исходом;

N^*_АС — количество полетов, в которых возникшие ОС завершились АС;

N^*_СС;N^*_УПП — количество полетов, в которых возникшие ОС могли быть классифицированы, соответственно, как СС и УУП.

Символы: «˄» — указывает на приближенный характер оценок;

«*» — указывает на то, что количество полетов опреде­лено на ограниченном интервале;

«N» — вероятность — определяется для осредненного ¹ полета

Если обозначить количество полетов, в которые не возникали ОС через N^*_бп(безопасные полеты), то, очевидно, должно соблю­даться условие:

Оценка вероятности возникновения той или иной ОС в течение осредненного часа полета вычисляется путем замены в формулах (1.1) — (1*4) знаменателя на величину Г_н — суммарное время поле­тов, выполненных в течение выбранного календарного периода.

Так, вероятность возникновения КС в течение осредненного часа полета оценивается как

а вероятность возникновения АС

Здесь индекс «Г» указывает на то, что вероятность определяется для осредненного часа полета.

По ряду причин критерии типа (1.1) — (1.4) (вероятность возник­новения той или иной ОС в осредненном полете) предпочтитель­ней критериев типа (1.7) —(1.8) (вероятность возникновения ОС в течение осредненного часа полета). Во-первых, размерность кри­териев (1.1) — 11.4) строго соответствует классическому определению вероятности, тогда как размерность критериев типа (1.7) — (1.8) выражается как «полет»; такая размерность больше подходит плотности вероятности, т. е. вероятности события, отнесенной к единице времени.

Во-вторых, что более важно, время полета с позиций безопас­ности не однородно и не равноценно. Существуют этапы полета, притом весьма скоротечные, для которых характерны высокая ве­роятность летных происшествий, и наоборот, ряд этапов являются малонапряженными. Использование критериев типа (1.7) — (1.8) нивелирует эти различия, что может исказить физическую картину явления и привести даже к ошибочным выводам.

10. Понятие адекватности АТ. Информационная, динамическая и эргономическая адекватность.

Применительно к задачам и методам имитационного моделиро­вания наиболее подходящим понятием, оценивающим сходство исходного и имитируемого объекта, следует считать адекватность [19]. Этот термин означает воспроизведение в имитируемом объекте результирующих функций, а также внешних и внутренних связей, соответствующих исходному объекту с такой точностью, которая достаточна для решения «оставленных задач в необходимом объеме, при этом отличие результата от требуемого должно лежать в поле назначенного допуска.

Если применить все вышеизложенные положения к задачам обучения экипажей ЛА на наземных имитационных средствах, то ясно, что тренажер в целом может считаться адекватным соответствующему ЛА, если приобретенные с его помощью навыки и умения пилотирования эквивалентны получаемым в реальном полете. Таким образом, условия эквивалентности навыков (умений) должны быть положены в основу формирования требований к адекватности на высшем комплексном уровне.

Можно выделить следующие основные компоненты общей адек­ватности тренажера (рис. 4.2):

адекватность целей и условий;

адекватность интерьера (рабочих мест членов экипажа); адекватность информационных потоков; динамическую адекватность; эргономическую адекватность; психологическую адекватность.

11. Летная годность и эргономическое обеспечение безопасности полета.

12. Основные имитаторы ЛА, имитатор динамики полета.

Основная литература.

МИИ

1. Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982, - 432с.

2. Змитрович А.И. Интеллектуальные информационные системы. – Мн.: НТООО «ТетраСистемс», 1997.- 361 с.

ИОС

1. Интеллектуальные обучающие системы: учеб. пособие/А.А. Бессонов, В.Я. Мамаев,

П.П. Парамонов. – СПб.: ГУАП, 2016. – 172 с.

АТ

1. Меерович Г.Ш., Годунов А.И., Ермолов О.К. Авиационные тренажеры и безопасность полетов. – Под ред. Мееровича Г.Ш. – Воздушный транспорт, 1990. – с. 343.

2. Учебник механика военно-воздушных сил. Авиационные тренажеры. М.

Модели представления знаний

На рис. 2.10 приведена классификация моделей представления знаний.

В процедурных моделях логическая модель реализует как объекты, так и правила с помощью предикатов первого порядка, является строго формализованной, использующей с универсальный дедуктивный и монотонный метод логического вывода «от цели к данным».

Рис. 2.10. Классификация моделей представления знаний

Под предикатом понимается логическая функция на N – аргументах (признаках), которая принимает истинное или ложное значение в зависимости от значений этих аргументов.

Продукционные модели используются для решения более сложных задач, которые основаны на применении эвристических методов представления знаний, позволяющих настраивать механизм вывода на особенности ПрО и учитывать неопределенность знаний.

В такой модели основной единицей знаний служит правило в виде

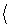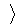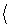«если «посылка» , то «заключение» »,

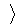с помощью которого могут быть выражены пространственно-временные, причинно-следственные, функционально-поведенческие (ситуация – действие) отношения объектов. Эта модель предназначена, главным образом, для описания последовательности различных ситуаций или действий и в меньшей степени для структурированного описания объектов.

Для логической модели характерна строгость формального аппарата получения решения. Однако полный последовательный перебор всех возможных решений может приводить к комбинаторным взрывам, в результате чего решение поставленных задач может занимать недопустимо много времени. Работа с неопределенностями знаний должна быть запрограммирована в виде самостоятельных метаправил, что на практике затрудняет разработку БЗ с помощью логического формализма.

Семантическая сеть отображает разнообразные отношения объектов.

Фреймовая модель как частный случай семантической сети использует для реализации операционного знания присоединенные процедуры.

Объектно-ориентированная модель как развитие фреймовой модели, реализуя обмен сообщениями между объектами, в большей степени ориентирована на решение динамических задач и отражение поведенческой модели.

Для обработки неопределенностей знаний продукционная модель использует, как правило, либо методы обработки условных вероятностей (байесовский подход), либо методы нечеткой логики.Такой подход предполагает начальное априорное задание некоторых гипотез (значений достигаемых целей), которые последовательно уточняются. С учетом вероятностей формируются апостериорные вероятности.

Для байесовского подхода к построению продукционной БЗ характерна большая трудоемкость статистического оценивания априорных шансов и факторов достаточности и необходимости.

Логические модели

Одним из методов представления знаний является логический метод, в основе которого лежит логика пре­дикатов [28]. Удобство его использования заключается в том, что свойственный ему механизм вывода, во-первых, допускает высокую степень формализации и обладает привычными математическими свойст­вами, и, во-вторых, может быть непосредственно за­программирован.

Одним из центральных вопросов логики предикатов является вопрос о том, можно ли из не­скольких исходных логических формул получить конеч­ную. Например, можно ли из каких-либо предпосылок вычислить заключение.

Логика предикатов является обобщением и рас­ширением логики высказываний, а высказывание яв­ляется центральной категорией логики предикатов.

Высказыванием называют предложение, которое мо­жет принимать одно из двух значений: истина или ложь.

Логика предикатов имеет свои синтаксис и алфа­вит. Алфавит обычно состоит из символов шести типов, обозначаемых буквами без индексов или теми же буквами с индексами:

1. Переменные: х, у, z, и 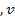, w.

2. Константы: а, b, с, d, e .

3. Функциональные символы: f, g, h .

4. Предикативные символы: р, r, s, t .

5. Логические символы:Ù, Ú, Ø, É, $, ";

6. Вспомогательные символы: запятые, скобки, иначе символы, не входя­щие в первые пять групп.

Предикативные символы служат для описания свойств объектов предметной области и отношений между ними.

При построении ИОС строится последовательность проведения работ по преобразованию предметно-ориентированного языка в язык предикатов, т. е. демонстрируется сведение контекстно-зависимого (естественного языка человека) предметно-ориентированного языка к машинно-представимому, что является основой для построения ОС, в которых реализуется возможность интеллектуального управления процессом обучения.

Продукционные модели

Продукционный метод является наиболее рас­пространенной моделью представления знаний в экс­пертных системах [14, 28 ]. В его основе лежат так называемые продукционные правила, или продукции, которые с помощью импликации связывают факты: «если A, то B». Правила устанавливают связь между фактами (знаниями вида «A это A»), содержащимися в условной части (А), и фактами, находящимися в заключительной его части (В).

Часто конкретные факты описывают состояния (человек или искусственная система формирования понятий). Объекты можно различать по тем значениям, которые имеют характеризующие их признаки, или атрибуты, т. е. те неотъемлемые свойства объекта (предмета), без которого тот не может существовать.

Применительно к воздушной навигации определение траектории звучит следующим образом: «траектория полета – пространственная линия, описываемая центром масс летательного аппарата при движении».

Системы, основанные на продукционном методе пред­ставления знаний, называют продукционными (рис. 2.11).

Рис.2.11. Фрагмент продукционной системы

Эти системы включают в себя три обязательных компонента: базу правил, базу данных, или рабочую память, и интерпретатор, или механизм вывода.

База правил (БП) является частью базы знаний и состоит из набора продукций (правил вывода). База данных (БД) содержит множество фактов, описывающих исходную ситуацию, заданную пользователем системы, а также факты, выведенные из исходных при срабатывании правил, т. е. являющиеся заключением этих правил. Механизм вывода осуществляет просмотр фактов в базе данных и сопоставление их с фактами из условной части правил, находящихся в базе правил, а также определяет порядок просмотра этих правил. Если при просмотре какого-либо правила окажется, что все факты из его условной части имеются и в базе данных, то условная часть правила считается истинной, в противном случае она считается ложной. Так просматриваются все правила и факты.

Семантические сети и графы

Важным шагом на пути выявления структуры, при­сущей знаниям, является построение моделей, в которых в явной форме выделены объекты, образующие её структуру [14, 28]. В основе таких моделей лежит понятие сети, состо­ящей из вершин, или узлов, соединенных дугами. С вершинами этой сети сопоставляются понятия (объекты, события, процессы, явления и др.), а с дуга­ми – связи, или отношения, существующие между этими понятиями.

Графическое изображение элемен­тов сети произвольное. Объекты могут изображаться точками, кружками, прямоугольниками и другим образом, дуги могут быть прямыми, ломаными, кривы­ми линиями.

Семантические сети (СС), с одной стороны, имитируют понимание естественного языка человеком, а с другой, придают фактическим знаниям графовую структурированную организацию, они представляют собой так называемые ориентиро­ванные графы [14]. Построение СС как графа помогает осмыслению знаний, способствует их конкре­тизации, выявлению противоречий, обнаружению не­достающей информации и т. п.

В качестве понятий СС обычно выступают абстрактные или конкретные объекты. Тип отношений может быть самым разным, что позволяет в достаточной мере обеспечить в них такой признак знаний, как связность. В общем случае это означает, что в виде СС можно отобразить знания, заключенные в текстах на естественном языке.

В этом примере передаются отноше­ния «абстрактное» – «конкретное» и свойства объектов, их функциональные связи.

Рис. 2.12. Представление определения угловой скорости разворота с помощью семантической сети

Семантические отношения могут быть условно разделены на четыре класса: лингвистические, логические, теоретико-множественные и квантификационные.

В общем случае СС должна обес­печивать:

– хранение сведений о понятиях и связях между ними;

– возможность поиска понятий по заданным характеристикам (связям с другими понятиями);

– возможность пополнения и кор­ректировки знаний системы в процессе обучения (ввод новых понятий, установление новых связей, удаление существующих понятий и связей);

– возможность осуществления процедуры обобщения и конкретизации знаний; – отражение иерархичности предметных знаний;

– понятность для эксперта – специалиста в ПрО [14].

Фреймовые модели представления знаний

Как уже отмечалось, высокая степень произвольности получаемых структур и многообразие типов вершин и связей при представлении знаний методом семантических сетей требуют боль­шого разнообразия процедур обработки информации, что существенно усложняет программное обеспечение. Это обстоятельство обусловило появление особых типов семантических сетей – фреймов.

Термин «фрейм» (от англ. frame – рамка) был предложен М. Минским, который описывает его следующим образом: «Фрейм является структурой данных для представления стереотип­ной ситуации. С каждым фреймом ассоциирована информация разных видов. Одна ее часть указывает, каким образом следует использовать данный фрейм, другая — что предположительно может повлечь за собой его выполнение, третья – что следует предпри­нять, если эти ожидания не подтвердятся» [29].

Фрейм, как и семантическая сеть, является набо­ром понятий и отношений между ними. Но в системе, основанной на фреймах, в отличие от системы, построенной на семантических сетях, понятие в каждой вершине определяется набором атрибутов и значения­ми. Указанные атрибуты как раз и являются слотами .

Под фреймом обычно понимают некоторую струк­туру вида

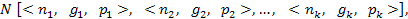
где N – имя фрейма; тройка 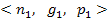– его i-й слот; n_i – имя слота; g_i – его тело; p_i – имя процедуры. Схематично это можно представить следующим образом (рис. 2.15):

Имя фрейма
Слот 1
Слот 2
Слот k

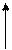
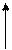
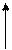
Имя Указатель Указатель Указатель Значение Присоединённая

слота наследования атрибутов слота типа данных слота процедура

Рис. 2.15. Схематическое изображение фрейма

Фрейм – это имеющий имя набор сло­тов, которые и содержат все необходимые знания. В общем случае слот имеет указанную ранее струк­туру, в частных случаях некоторые элементы этой структуры могут не учитываться.

Указатель наследования служит для передачи иерар­хических отношений. Фрейм, расположенный на более высоком уровне, называют фреймом – родителем. В свою очередь фрейм, расположенный на более низком уровне, называют дочерним фреймом. Слоты фреймов раскрывают их содержание.

В качестве атрибутов слотов могут выступать тексты, числа, процедуры, указатели (метки) на определенные блоки информации из общей базы знаний системы (т. е. компьютерной про­граммы) и др.

С каждым слотом фрейма можно связать любое число присоединенных процедур. Они могут работать как безусловно, так и по какому-либо условию. Безус­ловную процедуру называют демоном, она выполняется всегда, когда слот становится активным, т. е. когда при работе системы на этот слот передается управле­ние.

Условные процедуры чаще всего бывают трех типов: «если – добавлено», «если –удалено», «если – нужно». Как правило, в состав слота они входят вместе.

Свойство вложенности, возможность иметь в ка­честве значений слотов ссылки на другие фреймы и другие слоты того же фрейма обеспечивает фреймовому методу представления знаний возможность удовлетво­рять требованиям структурированности и связности знаний.

В общем случае модель представления знаний в виде фреймов строится в форме сети, т. е. системы определенным образом взаимосвязанных фреймов. Тип связи имеет характер переходов, иначе говоря, подобен гипертексту. На рис. 2.18. представлена сеть из трех фреймов

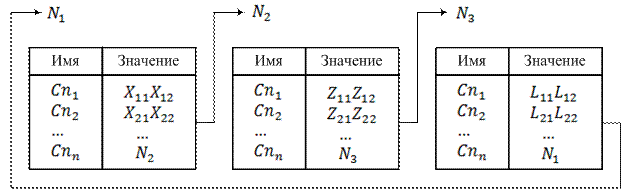
Рис. 2.18. Сеть фреймов

3. Вывод на знаниях. Машина вывода

Системы нечёткого вывода, основные этапы нечеткого вывода

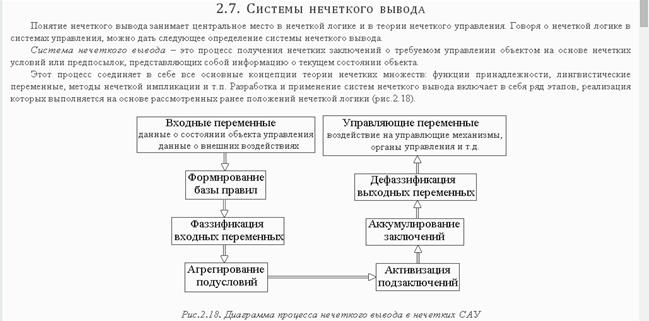
Алгоритмы нечеткого вывода

Алгоритм Мамдани (Mamdani) нашел применение в первых нечетких системах автоматического управления. Был предложен в 1975 году английским математиком Е.Мамдани для управления паровым двигателем.

· Формирование базы правил системы нечеткого вывода осуществляется в виде упорядоченного согласованного списка нечетких продукционных правил в виде «IF A THEN B », где антецеденты ядер правил нечеткой продукции построены при помощи логических связок «И», а консеквенты ядер правил нечеткой продукции простые.

· Фаззификация входных переменных осуществляется описанным выше способом, так же, как и в общем случае построения системы нечеткого вывода.

· Агрегирование подусловий правил нечеткой продукции осуществляется при помощи классической нечеткой логической операции «И» двух элементарных высказываний A, B : T(A ∩ B) = min{ T(A);T(B) } .

· Активизация подзаключений правил нечеткой продукции осуществляется методом min-активизации μ (y) = min{c; μ (x) } , где μ (x) и c – соответственно функции принадлежности термов лингвистических переменных и степени истинности нечетких высказываний, образующих соответствующие следствия (консеквенты) ядер нечетких продукционных правил.

· Аккумуляция подзаключений правил нечеткой продукции проводится при помощи классического для нечеткой логики max-объединения функций принадлежности ∀ x ∈ X μ A B x = max{ μ A x ; μ B x } .

· Дефаззификация проводится методом центра тяжести или центра площади.

Например , описанный выше случай управления уровнем бака соответствует алгоритму Мамдани, если на этапе дефаззифик