Условия равновесия системы сил.

Введение

Теоритической механикой называется наука изучающая, законы механического движения материальных тел и устанавливающая приемы и методы решения задач связанных с этим движением.

Теоритическая механика базируется на физике и математике и служит фундаментом для таких дисциплин, как сопротивление материалов и деталей машин.

Три эти дисциплины образуют единый курс, который образует курс технической механики.

Теоритическая механика состоит из 3-х разделов:

1.Раздел механики в котором изучаются условия равновесия тел-статика

2.Раздел механики в котором изучают движение материальных тел, без учета действующих на них тел-кинематика

3.Раздел механики в котором изучают взаимосвязи между движениями материальных тел и действий на них- динамика.

Статика

Частицы тела размерами которого можно пренебречь принимают за материальную точку. В механике все тела представляются как систему материальных точек.

Тело у которого расстояния между частицами во всех случаях остаются неизменными принимают за абсолютно твердое, как правило в теоритической механике рассматривают тела абсолютно твердые, а в сопротивлении материалов-деформируемые.

Сила-это мера механического взаимодействия тел характеризующая величину и направление, этого взаимодействия. Сила величина векторная.

Действие силы на тело характеризуется 3-мя элементами:

1.точкой приложения силы, а для абсолютно твердых линия движения

2.направлением

3.численным значениям

N Сила F приложенная в точке А изображается отрезком длиной l, отложенным от точки А, точка А называется началом силы F. Прямая М, N называется линия действия силы. РСУНОК!

Сила эквивалентная системе сил т.е оказывающая на тело такое же действие как и система сил- называется равнодействующей.

Сила после присоединения которой тело приходит в состояние покоя или начинает двигаться прямолинейно и равномерно называется уравновешивающей.

Если одну систему сил можно заменить другой системой и нарушая их действие на тело, то такие называются статическими эквивалентными.

Аксиомы статики

1,Законы инерции

Всякая изолированная материальная точка находится в состоянии покоя или движется равномерно и прямолинейно до тех пор пока внешние силы не выведут ее из этого состояния.

2,Условие равновесия 2-х сил

2-ве силы приложенные к абсолютно твердому телу образуют уравновешенную силу только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны. Эта аксиома верна для абсолютно твердых тел или для гибких тел только в случае растяжения.

3,Действие данной системы сил не нарушится если к ней добавить или от нее отнять уравновешенную систему сил.

Следствие 1 РИСуНОК

Предположение, что твердое тело находиться в равновесии под действием силы F приложенной в точке В. Возмем на линии действия силы какую нибудь точку А и приложим в этой точке 2-ве силы F1 и F2 числено равные силе F. Силу F1 направим по линии действия сил, а силу F2 в противоположную сторону т.к силы F1 и F2 взаимо уравновешиваются то от их присоединения равновесия тела не нарушается. Но силы F1 и F2 так же взаимо уравновешиваются следовательно не нарушая равновесие их можно отбросить таким образом получим одну силу F1 которой заменена первоначально сила F.

Силу приложения к твердому телу можно переносить вдоль линии ее действия в любую другую точку действия силы на тело при этом не изменяется.

Следствие 2

Равнодействующая и уравновешивающая силы всегда равны по величине и направлены по одной прямой в противоположную стороны.

Аксиома 4 РИСУНОК

Правило параллелограмма

Равнодействующая 2-ух сил приложенная в одной точке, приложена в той же точке и изображается диагональю параллелограмма по строенных на этих силах как на сторонах.

Аксиома 5

Закон действия и противодействия.

Два твердых тела всегда взаимодействуют друг с другом с силами равными по величине, но противоположным по направлению.

Связи и их реакции.

Все тела можно разделить на свободные и не свободные. Свободными называются тела, которые в любой момент времени могут получать любое перемещение. Тела у которых ряд перемещений ограничен, называются не свободными. Тела ограничивающие свободу перемещения данных тел называются связями. Сила с которой связь действует на опору называется реакцией связи.

1,Гладкая поверхность (РИСУНОК)

Реакция гладкой поверхности направленна по общей нормали по поверхности соприкасающихся тел.

Реакция гладкой поверхности всегда перпендикулярна данной поверхности. При опоре балке на угол реакция перпендикулярна балке.(РИСУНОК)

2,Цилиндрический шарнир

При нахождении реакции цилиндрического шарнира вначале определить 2-ве взаимо перпендикулярные составляющие которой задаются, а затем по формуле находим саму реакцию.

3,Шарнирно закрепленные стержни(РИСУНОК)

Реакции шарнирно закрепленных стержней направлены вдоль стержней если они прямые и вдоль прямой соединенных осей шарнира если они кривые.

4,Гибкие связи (РИСУНОК)

Реакции гибких связей всегда направлены вдоль связей от тела.

5,Неподвижная шарнирная опора (РИСУНОК)

При решении задач реакции неподвижной шарнирной опоры изображаются в виде 2-х составляющих Rax и Ray в произвольном направлении.

6,Подвижная шарнирная опора(РИСУНОК)

Реакция подвижной шарнирной опоры перпендикулярна поверхности по которой могут перемещатся катки на которых установлена опора.

7,Жесткая заделка(РИСУНОК)

Реакция изображается в виде 2-х составляющих сил, а также пары сил с неизвестным моментов МА.

Сложение сходящихся схем.

Система сил называется сходящейся если линия действия всех сил пересекаются в одной точке.

R=F1+F2+F3+F4+Fn

Существуют геометрический способы сложения и аналитический:

Геометрический способ:

1,Две силы складываются на основе аксиомы параллелограмма сил

2,Равнодействующая 3-х сил изображается диагональю параллелограмма пространственного

3,Произвольное число сил складывается на основе построения силового многоугольника

Аналитический способ: равнодействующая равна сумме всех сил R=

В проекциях на оси координат получим : Rx=

Ry= R=

Rz=

Условие равновесия сходящихся сил:

1,Для равновесия системы сходящихся сил необходимо что бы силовой многоугольник построенный на этих силах был замкнут.

2,Силы приложенные в одной точке находятся в равновесии, если их равнодействующая равна нулю.

R=0=> Rx=Ry=Rz=0

Проекция силы на ось(РИСУНОК)

Проекция силы на ось называется произведение модуля сил на cos угла между силой и осью.

Момент силы относительно центра (РИСУНОК)

Плоскость проходящая через силу и центр О называется плоскостью поворота т.е сила стремится повернуть тело вокруг точки О.

Плечом силы относительно центра О называется перпендикуляр опущенный из центра О на линию действия силы.

Моментом силы относительно центра О называется вектор перпендикулярный плоскости поворота, равный по модулю , произведению ,модуля силы на плечо и направленный в ту сторону откуда направление поворота силы видно против хода часовой стрелки.

Mo(F)=F*h

Момент равнодействующей равен сумме моментов составляющих сил

Mz(R)=mz(F1)+mz(F2)

Пара сил, момент пары сил.

Парой сил называется совокупность двух сил равных по величине параллельной и направленных в разные стороны.(РИСУНОК)

Пара сил моделирует такое воздействие на тело, которое может привести к его вращению плечам пары сил называется расстояние между линиями действия сил пары.

Момент пары сил называется вектор перпендикулярный плоскости действия пары сил, равный по модулю произведению и направленный в ту сторону откуда поворот пары сил виден против хода часовой стрелки.(РИСУНОК)

Будем считать момент больше 0, если пара стремиться повернуть тело против хода часовой стрелки, в противном случае момент будет больше нуля: когда стрелка против хода часовой стрелки, и отрицательный по часовой.

Классификация системы сил

Различают плоские и пространственные силы. Система сил называется плоской если линия действия сил лежат в одной плоскости, в противном случае система сил: сходящихся , параллельных , произвольно расположенных.

Если линия действия сил пересекаются в одной точке то имеет место система сходящихся сил.

Если линия действия сил параллельны то имеет быть система параллельных сил.

Если систему сил не удается свести не к системе параллельных сил, не к системе сходящихся сил то имеет место произвольная система сил.

Равновесие системы тел.

Определение внутренних сил.

Системой тел называется совокупность нескольких тел соединенных между собой шарнирами, нитями и т.д.

(РИСУНОК)

Рассмотри равновесие конструкций состоящих из 2-ух частей соединенных шарниром через шарниром правая часть конструкции воздействует на левую часть силой Rс по аксиоме действия и противодействия, левая часть конструкции воздействует на правую часть с силой Rc’. Если рассматривать равновесие конструкции в целом то внутренние силы Rс и Rc’ не могут быть найдены из уравнения равновесия. Соответствующие слогаемые сокращаются и число внешних сил Rax, Ray, Rbx , Кин превышает число уравнений равновесия левой части конструкций с учетом от брошенной правой части.

(РИСУНОК)

Затем рассмотрим равновесие правой части конструкции с учетом воздействия отброшенной левой части.

(РИСУНОК)

Внутренние силы при этом в уравнениях не сокращаются и при этом смогут быть определенны число уравнений возрастает до 6, что соответствует числу не известных сил, система становится статически определенной.

Центр тяжести

(РИСУНОК)

Пусть тело находиться в гравитационном поле земли, разобьем его на несколько частей и приложим к каждой части соответствующую силу тяжести силы Р1,Р2,Рn образуют пространственную систему перпендикулярных сил. Найдем равнодействующую этих системы сил т.е. модуль этой силы и точку приложения. Модуль равнодействующей определяется по формуле:

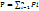(1)

Модуль силы определяется по формуле называется весом тела. Положение точки приложения силы определяется по формуле:

rc= 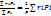(2)

Положение точки С относительно к телу не зависит от ориентации тела в гравитационном поле. Геометрическая связь с телом т.е. точкой через которую проходит равнодействующая силы тяжести частиц тела при любой его ориентации в любом поле называется центром тяжести тела. Проецируя уравнения 2 на оси координат получим координаты центра тяжести:

Xc=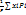

yc= 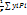(3)

zc=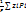

Тело называется однородным если его плоскость по всему объему тела постоянна:

Pi=ρ*Vi (4)

ρ-удельный вес

Vi-Объем I частицы весом Pi

Для однородных тел ρ=const (5)

Преобразуем формулу (3)

Xc=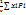

yc= 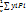(6), Где V=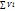

zc=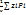

Из уравнения (6) следует, что положение центра тяжести не зависит от материала из которого изготовленно тело, а определяется лишь формой тела. Поэтому точку определяемую по уравнениям (6) называют центром тяжести объема. Для пластины постоянной толщины получим:

Xc=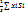

yc= 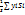(7)S- площадь всей пластины.

Точку определяемую по формуле (7) называют центром тяжести площади.

Способы определения положения центра тяжести.

Существует следующие способы: 1) использование симметрии

2) разбиение 3) экспериментальный

Способы используются для однородных тел.

1,Использование симметрии : если тело имеет плоскость, ось или центр симметрии то центр тяжести находиться в плоскости на оси или в центре симметрии. (РИСУНОК)

2,Разбиение: если тело удастся разбить на части положения, центров тяжести которых заранее известны то можно использовать формулы:

Xc= 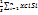, (8), N-число частей на которое разбито тело.

yc= 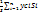, yci- координаты центров тяжести

Способ разбития можно распространить на тела имеющие вырезы, при этом площадь вырезом условно считается отрицательной.(РИСУНКИ)

Трение-скольжение

При стремлении передвинуть тело по шероховатости поверхности возникает трение скольжения.(РИСУНОК)

Предельная сила трения скольжения определяется по формуле :

Fпр=f*N

Величина этого коэфицента зависит от материала и состояния соприкасающихся частей. Если тело начало передвигаться по шероховатой поверхности то величина силы трения скольжения определяется

Fтр=f*N

Его величина зависит от материала, состояния соприкасающихся частей и в малой степени зависит от скорости тела.(РИСУНОК)

При решении задач с четом трения скольжения обычно рассматривают предельный случай равновесия. В этом случае сила трения скольжения достигает своего предельного значения.

Сила трения-качения

Трение качение называется сопротивление возникающие при качании одного тела по поверхности другого. Рассмотрим круглый цилиндрический каток радиусом R и весом P лежащий на горизонтальной шероховатой поверхности(РИСУНОК)

На рис 91) изображен идиальный случай, когда каток не деформирует поверхность качения обеспечивается парой сил F и Fтр. При любой какой угодно малой силе F. На рис (2) изображен реальный случай когда поверхность деформируется. При этом сила N смещается относительно осей симметрии на величину К. Возникает пара сил P и N. Препятствующая качению катка. Плечо этой пары называется коэфициентом трения-качения. Условием при котором обеспечивается качением катка записывается следующим образом(РИСУНОК)

Теорема Гюгенса

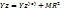Момент инерции тела относительно оси равен моменту инерции тела оси параллельной данной оси и проходящих через центр масс тела сложенной с произведением массы тела на квадрат расстояния между осями. Ось проходящая через центр масс называется центральной. Центробежные моменты системы определяются:

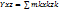
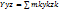
Кинетическая энергия.

Кинетическая энергия материальной точки называется половина произведения массы точки на квадрат ее скорости.

Кинетической энергией механической системы называется сумма кинетической энергии материальных точек.

Работа силы

Элементарная работа силы называется скалярное произведение силы на прилежащий радиус точки.

Работы силы на не котором перемещении определяется как сумма элементарных работ этой силы вычесленных на данном перемещении.

Работа силы зависит от траектории движения точки по существующей силе работа которых не зависит от этой траектории, а зависит от начального и конечного положения точки.

1,Работа простой сила в случае когда точка приложения силы движется прямолинейно. A1,2=FScosα

2,Работа силы тяжести

A1,2= +- P*дельтаH

3,Работа силы упругости пружины A1,2=c/2(

4,Работа сил приложенных к вращающемуся телу

5,Работа момента силы трения качения

A1,2=-K*N*S/P

В общем случае работа сила больше 0 если сила помогает движению и меньше 0 если сила препяствует движению.

6,Работа внутренних сил действующих на абсолютно твердое тело на любом перемещении тела равно 0

Скорость точки.Метод полюса

Поожение любой точки плоской фигуры опред. тремя пар-ми коодинатами XY и углом поворотв фи. Для определения скорости и ускорения любой точки плоской фигуры достаточно знать след.величины:скорость и ускорение полюса, угловую скорость и угл.усл. Точку "о" назовем полюсом . За полюс мжно выбирать любую точку тела, но удобнее выбирать ту точку скорость и ускорение которой заранее известны.

Плоское движение может быть представлено из двух движении происходящих одновременно вокруг полюса.

Скорость любой точки плоск.фигуры явл. сумме скорости полюса и скорости точки, прии ее вращении вместе с плоск.фигурой вокруг полюса направлен в соотв с направл угл.скорости и равен по модулю произв. угл.скорости на рассст. от точки до полюса.

Сложное движение

Пустьь точка М движется от-но системы координат, а сама системв движется вокруг неподвижноф системы , тогда движение тотчки М от-но еподвижной системы назыв.слодным движением.

Движение точки М от-но подвижной системы назыв. относительным движением. Скорость и ускорение точки от-но этой скороти нызыв. отн. скоростью т отн. движение, вместе с подвижной системы.

Движение точкт М отно-но системы назыыобсол. движением.

Скорость и ускорение точки от-но этой системы называется абсолютной скоростью и абсолютным ускорением. Чтобы наблюдать это движение, человек должен находиться в неподвижной системе координат. Движение подвижной системы координат относительно неподвижной системы называется переносным движением.

Переносной скоростью и переносным ускорением точки называются скорость и ускорение той точки подвижной системы координат, которой в данный момент времени совпадает с движущейся точкой, обозначается так Ve и Ae. Для определения переносной скорости и переносного ускорения мысленно остановим относительно движения и будем считать, что точка не движется относительно подвижной системы, а только перемещается вместе с ней.

Теорема сложения скоростей.

Абсолютная скорость точки равна геометрической сумме относительной и переносной скорости.

Теорема сложения ускорений.

Абсолютной ускорение точки равно геометрической сумме относительного ускорения переносного ускорения и ускорения Ирлонца. При решение задач, относительное и переносное ускорение представляется в виде суммы двух слагаемых: касательного и нормального ускорения.

Введение

Теоритической механикой называется наука изучающая, законы механического движения материальных тел и устанавливающая приемы и методы решения задач связанных с этим движением.

Теоритическая механика базируется на физике и математике и служит фундаментом для таких дисциплин, как сопротивление материалов и деталей машин.

Три эти дисциплины образуют единый курс, который образует курс технической механики.

Теоритическая механика состоит из 3-х разделов:

1.Раздел механики в котором изучаются условия равновесия тел-статика

2.Раздел механики в котором изучают движение материальных тел, без учета действующих на них тел-кинематика

3.Раздел механики в котором изучают взаимосвязи между движениями материальных тел и действий на них- динамика.

Статика

Частицы тела размерами которого можно пренебречь принимают за материальную точку. В механике все тела представляются как систему материальных точек.

Тело у которого расстояния между частицами во всех случаях остаются неизменными принимают за абсолютно твердое, как правило в теоритической механике рассматривают тела абсолютно твердые, а в сопротивлении материалов-деформируемые.

Сила-это мера механического взаимодействия тел характеризующая величину и направление, этого взаимодействия. Сила величина векторная.

Действие силы на тело характеризуется 3-мя элементами:

1.точкой приложения силы, а для абсолютно твердых линия движения

2.направлением

3.численным значениям

N Сила F приложенная в точке А изображается отрезком длиной l, отложенным от точки А, точка А называется началом силы F. Прямая М, N называется линия действия силы. РСУНОК!

Сила эквивалентная системе сил т.е оказывающая на тело такое же действие как и система сил- называется равнодействующей.

Сила после присоединения которой тело приходит в состояние покоя или начинает двигаться прямолинейно и равномерно называется уравновешивающей.

Если одну систему сил можно заменить другой системой и нарушая их действие на тело, то такие называются статическими эквивалентными.

Аксиомы статики

1,Законы инерции

Всякая изолированная материальная точка находится в состоянии покоя или движется равномерно и прямолинейно до тех пор пока внешние силы не выведут ее из этого состояния.

2,Условие равновесия 2-х сил

2-ве силы приложенные к абсолютно твердому телу образуют уравновешенную силу только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны. Эта аксиома верна для абсолютно твердых тел или для гибких тел только в случае растяжения.

3,Действие данной системы сил не нарушится если к ней добавить или от нее отнять уравновешенную систему сил.

Следствие 1 РИСуНОК

Предположение, что твердое тело находиться в равновесии под действием силы F приложенной в точке В. Возмем на линии действия силы какую нибудь точку А и приложим в этой точке 2-ве силы F1 и F2 числено равные силе F. Силу F1 направим по линии действия сил, а силу F2 в противоположную сторону т.к силы F1 и F2 взаимо уравновешиваются то от их присоединения равновесия тела не нарушается. Но силы F1 и F2 так же взаимо уравновешиваются следовательно не нарушая равновесие их можно отбросить таким образом получим одну силу F1 которой заменена первоначально сила F.

Силу приложения к твердому телу можно переносить вдоль линии ее действия в любую другую точку действия силы на тело при этом не изменяется.

Следствие 2

Равнодействующая и уравновешивающая силы всегда равны по величине и направлены по одной прямой в противоположную стороны.

Аксиома 4 РИСУНОК

Правило параллелограмма

Равнодействующая 2-ух сил приложенная в одной точке, приложена в той же точке и изображается диагональю параллелограмма по строенных на этих силах как на сторонах.

Аксиома 5

Закон действия и противодействия.

Два твердых тела всегда взаимодействуют друг с другом с силами равными по величине, но противоположным по направлению.

Связи и их реакции.

Все тела можно разделить на свободные и не свободные. Свободными называются тела, которые в любой момент времени могут получать любое перемещение. Тела у которых ряд перемещений ограничен, называются не свободными. Тела ограничивающие свободу перемещения данных тел называются связями. Сила с которой связь действует на опору называется реакцией связи.

1,Гладкая поверхность (РИСУНОК)

Реакция гладкой поверхности направленна по общей нормали по поверхности соприкасающихся тел.

Реакция гладкой поверхности всегда перпендикулярна данной поверхности. При опоре балке на угол реакция перпендикулярна балке.(РИСУНОК)

2,Цилиндрический шарнир

При нахождении реакции цилиндрического шарнира вначале определить 2-ве взаимо перпендикулярные составляющие которой задаются, а затем по формуле находим саму реакцию.

3,Шарнирно закрепленные стержни(РИСУНОК)

Реакции шарнирно закрепленных стержней направлены вдоль стержней если они прямые и вдоль прямой соединенных осей шарнира если они кривые.

4,Гибкие связи (РИСУНОК)

Реакции гибких связей всегда направлены вдоль связей от тела.

5,Неподвижная шарнирная опора (РИСУНОК)

При решении задач реакции неподвижной шарнирной опоры изображаются в виде 2-х составляющих Rax и Ray в произвольном направлении.

6,Подвижная шарнирная опора(РИСУНОК)

Реакция подвижной шарнирной опоры перпендикулярна поверхности по которой могут перемещатся катки на которых установлена опора.

7,Жесткая заделка(РИСУНОК)

Реакция изображается в виде 2-х составляющих сил, а также пары сил с неизвестным моментов МА.

Сложение сходящихся схем.

Система сил называется сходящейся если линия действия всех сил пересекаются в одной точке.

R=F1+F2+F3+F4+Fn

Существуют геометрический способы сложения и аналитический:

Геометрический способ:

1,Две силы складываются на основе аксиомы параллелограмма сил

2,Равнодействующая 3-х сил изображается диагональю параллелограмма пространственного

3,Произвольное число сил складывается на основе построения силового многоугольника

Аналитический способ: равнодействующая равна сумме всех сил R=

В проекциях на оси координат получим : Rx=

Ry= R=

Rz=

Условие равновесия сходящихся сил:

1,Для равновесия системы сходящихся сил необходимо что бы силовой многоугольник построенный на этих силах был замкнут.

2,Силы приложенные в одной точке находятся в равновесии, если их равнодействующая равна нулю.

R=0=> Rx=Ry=Rz=0

Проекция силы на ось(РИСУНОК)

Проекция силы на ось называется произведение модуля сил на cos угла между силой и осью.

Момент силы относительно центра (РИСУНОК)

Плоскость проходящая через силу и центр О называется плоскостью поворота т.е сила стремится повернуть тело вокруг точки О.

Плечом силы относительно центра О называется перпендикуляр опущенный из центра О на линию действия силы.

Моментом силы относительно центра О называется вектор перпендикулярный плоскости поворота, равный по модулю , произведению ,модуля силы на плечо и направленный в ту сторону откуда направление поворота силы видно против хода часовой стрелки.

Mo(F)=F*h

Момент равнодействующей равен сумме моментов составляющих сил

Mz(R)=mz(F1)+mz(F2)

Пара сил, момент пары сил.

Парой сил называется совокупность двух сил равных по величине параллельной и направленных в разные стороны.(РИСУНОК)

Пара сил моделирует такое воздействие на тело, которое может привести к его вращению плечам пары сил называется расстояние между линиями действия сил пары.

Момент пары сил называется вектор перпендикулярный плоскости действия пары сил, равный по модулю произведению и направленный в ту сторону откуда поворот пары сил виден против хода часовой стрелки.(РИСУНОК)

Будем считать момент больше 0, если пара стремиться повернуть тело против хода часовой стрелки, в противном случае момент будет больше нуля: когда стрелка против хода часовой стрелки, и отрицательный по часовой.

Классификация системы сил

Различают плоские и пространственные силы. Система сил называется плоской если линия действия сил лежат в одной плоскости, в противном случае система сил: сходящихся , параллельных , произвольно расположенных.

Если линия действия сил пересекаются в одной точке то имеет место система сходящихся сил.

Если линия действия сил параллельны то имеет быть система параллельных сил.

Если систему сил не удается свести не к системе параллельных сил, не к системе сходящихся сил то имеет место произвольная система сил.

Условия равновесия системы сил.

Если тело находиться в рановесия то либо оно является свободным, либо к нему приложена уравновешенная система сил и в том и в другом случае справедливо уравнения:

В проекциях на оси координат получим:

Рассмотрим условия равновесия различных систем сил. (РИСУНОК)

Если число не известных сил не превышают числа уравнений равновесия, которые могут быть написаны для данной системы сил, то такая система называется статическим.