Тема: Сложное сопротивление. Косой изгиб
Тема: Сложное сопротивление. Косой изгиб
Цель: На основе принципа суперпозиции получить расчетные формулы для косого изгиба, дать разъяснение по использованию их в практических расчетах. Разъяснить последовательность расчетов валов на изгиб с кручением с применение теории прочности.
Основные вопросы лекции:
Понятие о сложном сопротивлении.
Общие понятия о косом изгибе. Определение внутренних усилий при косом изгибе.
Определение напряжений и перемещении при косом изгибе и внецентренном растяжении сжатии.
Понятие о ядре сечения.
Расчет валов работающих на изгиб с кручением.
Литература:
Феодосьев В.И. § 28-29, 30, 33
Понятие о сложном сопротивлении.
На предыдущих лекциях мы рассмотрели простейшие виды деформаций: растяжение-сжатие, сдвиг, кручение, плоский изгиб, поперечный изгиб.
При этом в поперечных сечениях возникает только одно внутреннее усилие - продольная или поперечная сила, крутящий или изгибающий момент, за исключением плоского поперечного изгиба.
| Виды нагружения | Напряжения | Деформации |
 Растяжение Растяжение | 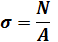 Условие прочности: Условие прочности: 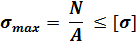 |  |
 Сдвиг Сдвиг |  Условие прочности: Условие прочности:  | 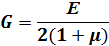 |
 Кручение Кручение | 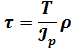 Условие прочности: Условие прочности: 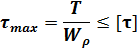 |  |
 Изгиб Изгиб | 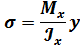 Условие прочности: Условие прочности: 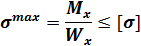 | 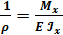  |
На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более.
Различные комбинации простых деформаций называются сложным сопротивлением.
 Сегодня приступаем к изучению сложного сопротивления.
Сегодня приступаем к изучению сложного сопротивления.
В общем случае нагружения бруса в его поперечных сечениях действуют шесть компонентов внутренних усилий (N, Qx, Qy, Mx, My, Mкр).
Косой изгиб– изгиб, при котором плоскость действия изгибающих моментов и поперечных сил не совпадает ни с одной из главных плоскостей инерции бруса.
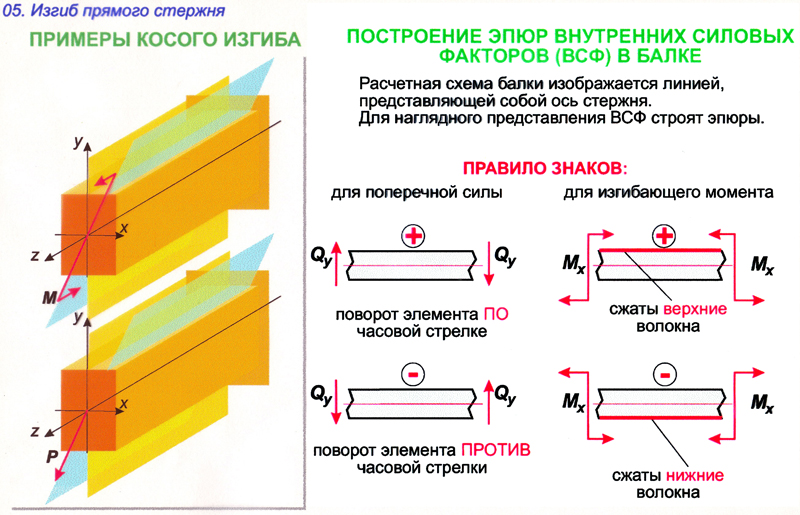 При косом изгибе изогнутая ось представляет собой плоскую кривую, и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки.
При косом изгибе изогнутая ось представляет собой плоскую кривую, и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки.
При пространственном изгибе нагрузка приложена в разных плоскостях, деформированная ось является пространственной кривой.
Для сечений, у которых монеты инерции относительно обеих ортогональных осей одинаковы, косой изгиб невозможен. У этих сечений все оси главные. Это сечения типа круг квадрат труба и т.п.
 Рассмотрим пример косого изгиба.
Рассмотрим пример косого изгиба.
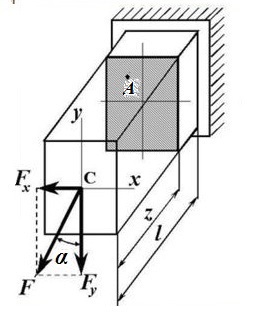
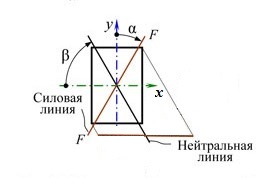
Пусть на консольную балку прямоугольного сечения действует сила F, приложенная в плоскости его торцевого поперечного сечения таким образом, что ее линия действия составляет угол α с главной центральной осью OY.
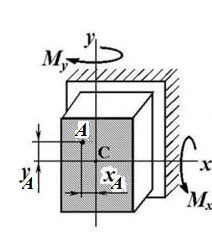 Разложим эту силу на составляющие Fx и Fу по главным осям ОХ и ОУ.
Разложим эту силу на составляющие Fx и Fу по главным осям ОХ и ОУ.
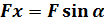
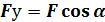
Данная формула позволяет определить напряжение в произвольной точке сечения.
Или
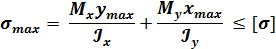
Нулевой или нейтральной линией называется геометрическое место точек поперечного сечения, в которых нормальные напряжения равны нулю.
Или


Отсюда найдем угол наклона нейтральной линии:
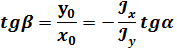
Уравнение нейтральной оси:

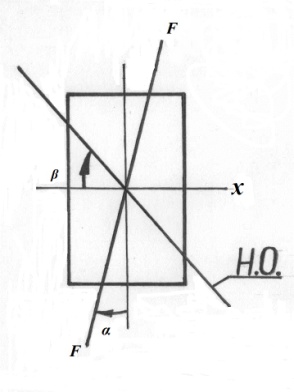 Анализируя полученное выражение , приходим к выводу, что в отличие от прямого изгиба нулевая и силовая линии не будут взаимно перпендикулярны
Анализируя полученное выражение , приходим к выводу, что в отличие от прямого изгиба нулевая и силовая линии не будут взаимно перпендикулярны
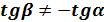
Лишь в частном случае, когда 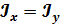 , угол между нулевой и силовой линиями будет прямым.
, угол между нулевой и силовой линиями будет прямым.
Нулевая и силовая линии проходят через разные квадранты сечений
 Свойства нейтральной линии
Свойства нейтральной линии
1. Если 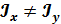 , то
, то 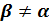 , то есть силовая плоскость и нейтральная линия не являются перпендикулярными.
, то есть силовая плоскость и нейтральная линия не являются перпендикулярными.
2. Если 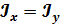 , то
, то 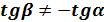 , то есть нейтральная линия и силовая плоскость перпендикулярны. В этом случае стержень испытывает плоский изгиб (примерами таких стержней являются стержни с сечением – круг, кольцо, квадрат).
, то есть нейтральная линия и силовая плоскость перпендикулярны. В этом случае стержень испытывает плоский изгиб (примерами таких стержней являются стержни с сечением – круг, кольцо, квадрат).
3. Знак «минус» в формуле указывает, что силовая плоскость и нейтральная линия при косом изгибе проходят через противоположные квадранты.
Для определения опасных точек сечения следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными .
Пример 1.
Подобрать прямоугольное сечение балки при условии, что h = 2b,[σ]= 160 МПа P= 60кН, α =30 ͦ, ℓ=2,8 м..
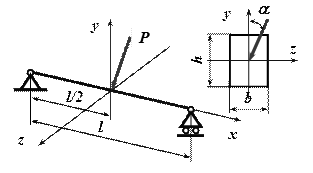
Решение:
Разложив силу P на две составляющие, действующие по направлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов Mz и My . Наибольшие моменты действуют в среднем сечении, где
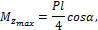
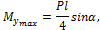
следовательно, это сечение является опасным.
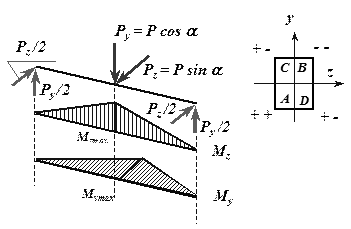
Эпюры изгибающих моментов к примеру 1
Для определения положения опасной точки расставим знаки от 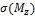 и
и 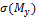 в угловых точках поперечного сечения балки. При действии момента
в угловых точках поперечного сечения балки. При действии момента 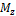 в точках A и D будут иметь место положительные (растягивающие) напряжения, а в точках C и B - отрицательные (сжимающие) напряжения. При действии момента
в точках A и D будут иметь место положительные (растягивающие) напряжения, а в точках C и B - отрицательные (сжимающие) напряжения. При действии момента 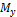 в точках A и C будут иметь место положительные
в точках A и C будут иметь место положительные 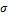 , а в точках B и D - отрицательные. Точки поперечного сечения A и B, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.
, а в точках B и D - отрицательные. Точки поперечного сечения A и B, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.
Судя по условию задачи, материал, из которого изготовлена балка, является пластичным ( 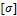 =160 МПа) и, следовательно, одинаково сопротивляется деформации растяжения и деформации сжатия. Таким образом, точки A и B являются равноопасными, и для них используется одно условие прочности
=160 МПа) и, следовательно, одинаково сопротивляется деформации растяжения и деформации сжатия. Таким образом, точки A и B являются равноопасными, и для них используется одно условие прочности
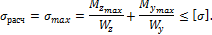
Вычислим моменты сопротивления сечения при заданном соотношении высоты и ширины
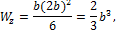
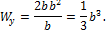
Подставляя в условие прочности выражения для изгибающих моментов и моментов сопротивления, получим:
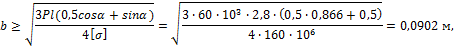
тогда h = 2b = 18,04 см.
Пример 2.
При установке на опоры двутавровой балки (№ 60: 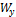 =182 см3,
=182 см3, 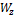 =2560 см3), предназначенной для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка и стенка двутавра отклонилась от вертикали на угол
=2560 см3), предназначенной для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка и стенка двутавра отклонилась от вертикали на угол 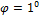 . Определить связанное с этим увеличение наибольших нормальных напряжений.
. Определить связанное с этим увеличение наибольших нормальных напряжений.
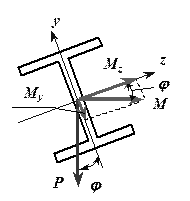
Появление внутренних изгибающих моментов
при косом изгибе.
Решение:
Отклонение оси двутавра (ось y) от вертикали привело к возникновению косого изгиба и появлению изгибающих моментов 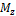 и
и 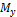 .
.
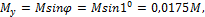
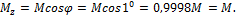
Максимальные напряжения при косом изгибе
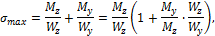
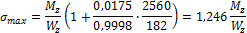
так как 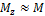 , то
, то 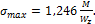
В случае правильной установки балки, сила P совпадала бы с вертикальной осью балки y, и имел бы место прямой изгиб, изгибающий момент был бы равен M , а напряжения
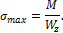
Таким образом, максимальные напряжения при косом изгибе за счет такого незначительного отклонения от вертикали возрастут на 24,6 %.
Тема: Сложное сопротивление. Косой изгиб
Цель: На основе принципа суперпозиции получить расчетные формулы для косого изгиба, дать разъяснение по использованию их в практических расчетах. Разъяснить последовательность расчетов валов на изгиб с кручением с применение теории прочности.
Основные вопросы лекции:
