Й способ. Инструмент анализа Регрессия.

1. Прежде чем мы начнем использовать этот инструмент, нужно убедиться, что был активизирован Пакет анализа (меню «Сервис» есть команда «Анализ данных»). Если нет, то выполните команду «Сервис/Надстройки». В диалоговом окне «Надстройки» установите флажок «Пакет анализа» и щелкните по кнопке ОК (в Excel 2007 этот инструмент находится на вкладке «Данные» - «Анализ данных»).

2. Далее выполните команду «Сервис/Анализ данных». Выберите инструмент анализа «Регрессия» из списка «Инструменты анализа». Щелкните по кнопке ОК.

3. На экране появится диалоговое окно «Регрессия» (рис. 7):

- в текстовом поле «Входной интервал Y» введите диапазон со значениями зависимой переменной $C$2:$C$211.

- в текстовом поле «Входной интервал Х» введите диапазон со значениями независимых переменных $В$2:$В$11.

-

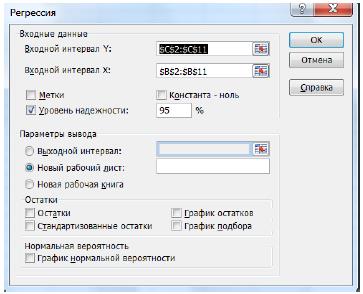Убедитесь, что в поле Уровень надежности введено 95% и переключатель «Параметры вывода» установлен в положении «Новый рабочий лист».

- Щелкните по кнопке ОК.

Рисунок 7. Диалоговое окно инструмента анализа «Регрессия»

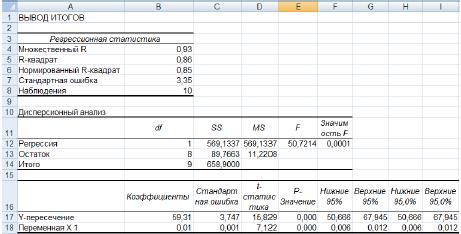Рисунок 8. Вывод итогов инструмента «Регрессия»

4. В результате на новом листе будет отображены результаты использования инструмента «Регрессия» (рис. 8).

5. Среди полученных результатов после применения инструмента Регрессия есть столбец «Коэффициенты», содержащий значение b в строке «Y-пересечение», а – в строке «Переменная Х1».

6. Сравним полученные результаты с ранее рассчитанными коэффициентами а и b - результаты полностью совпадают.

7. Следует обратить также внимание на следующие показатели:

а) Столбец «df» – число степеней свободы (используется при проверке адекватности модели по статистическим таблицам):

- в строке «Регрессия» находится k₁ – количество коэффициентов уравнения, не считая свободного члена b;

- в строке «Остаток» находится k₂ = n – k₁ – 1, где n – количество исходных данных.

б) Столбец «SS» (сумма квадратов):

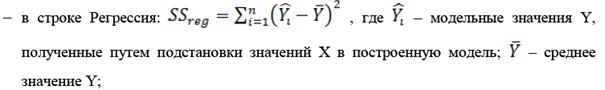д) Столбец «Значимость F» – оценка адекватности построенной модели. Находится по значениям F, и с помощью функции FРАСП. Если значимость F меньше 0,05, то модель может считаться адекватной с вероятностью 0,95.

е) «Стандартная ошибка», «t-статистика» – это вспомогательные величины, используемые для проверки значимости коэффициентов модели.

ж) «Р-Значение» – оценка значимости коэффициентов модели. Если «Р-Значение» меньше 0,05, то с вероятностью 0,95 можно считать, что соответствующий коэффициент модели значим (т.е. его нельзя считать равным нулю и Y значимо зависит от соответствующего Х).

и) Нижние и верхние 95% – доверительные интервалы для коэффициентов модели.

Рисунок 9. Исходные данные для прогнозирования

Контрольные вопросы

1. В чем цель корреляционного анализа?

2. Что такое коэффициент корреляции?

3. Для чего используется t-статистика Стьюдента?

4. Какими способами можно определить коэффициент корреляции в MS Excel?

5. В чем цель регрессионного анализа?

6. Опишите уравнение линейной регрессии.

7. Какими способами можно найти модель регрессии в MS Excel? Коротко опишите эти способы.

8. Что такое «целевая ячейка»?

9. Для чего используются относительные, абсолютные и смешанные ссылки в формулах?

10. Полный факторный план какого порядка целесообразно применить при 8 факторном эксперименте?

11. Чем отличаются уравнения регрессии в описании планов первого и второго порядка?

12. Для чего выполняется переход от натуральных размерных значений факторов к кодированным безразмерным?

1.2. Порядок выполнения задания

1. Перед выполнением задания 1 изучить теоретическую часть работы (1.1) и ответить на контрольные вопросы.

2. Открыть новую книгу Excel и сохранить под именем «Статфункции.хls».

3. В книге выполнить задание со следующими условиями:

Имеются данные по двум экономическим показателям X и Y:

Цена (X)

Спрос (Y)

Необходимо:

- вычислить коэффициент корреляции;

- построить корреляционное поле (диаграмма) на отдельном листе;

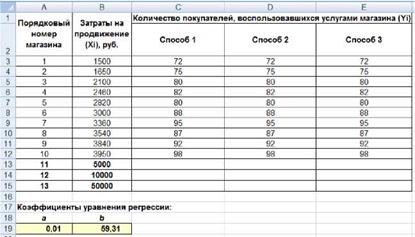
- построить регрессионную модель (с использованием функции ЛИНЕЙН);

- спрогнозировать значение Y для 3-х новых значений X с помощью функции ПРЕДСКАЗ. Все действия (в том числе форматирование таблицы) необходимо выполнять, опираясь на образец.

4. На диаграмме разместить линию тренда с уравнением регрессии и оформить их как показано в образце. Дополнить диаграмму спрогнозированными данными (кроме последнего значения цены 5000).

5. Используя инструмент «Регрессия» на отдельном листе построить регрессионную модель с учетом новых спрогнозированных значений. Записать на листе уравнение регрессии на основании данных из «Вывода итогов».

6. Представить файл с выполненной работой преподавателю для проверки.

1.3. Требования к оформлению, процедура зашиты

Отчет по данной работе должен содержать распечатку каждого листа книги «Статфункции.хls». При защите необходимо дать требуемые пояснения к содержанию каждого листа книги, продемонстрировать выполнение работы в файле книги «Статфункции.хls» и ответить на контрольные вопросы.

Лабораторная работа 3

Моделирование аналого-цифрового преобразования

Среди большого числа пакетов прикладных программ система МАТЛАБ (The Math Works Inc.) занимает особое место. Первоначально ориентированная на исследовательские проекты, система в последние годы стала рабочим инструментом не только ученых, но также инженеров-разработчиков и студентов. В сообществе радиоинженеров, управленцев, физиков и связистов МАТЛАБ получил необычайное распространение и по сути стал средством междисциплинарного и международного общения. Особенно широко, эффектно и эффективно система МАТЛАБ применяется в области обработки сигналов, которая по необходимости затрагивает информатику и связь, управление, радиолокацию и радионавигацию, радиовещание и телевидение, медицинское приборостроение и измерительную технику, автомобильную и бытовую электронику и многое другое. Не случайно в широком спектре вопросов, затронутых системой МАТЛАБ, приложениям, упомянутым выше, уделено особое внимание.

В действительности, система МАТЛАБ это огромный мир средств и возможностей решения разнообразных задач в различных областях человеческой деятельности. Построенная по единым принципам для разных предметных областей, МАТЛАБ одновременно является и операционной средой, и языком программирования. Для упрощения, прежде всего, технических решений в системе разработаны и продолжают развиваться:

• предметно ориентированный инструментарий TOOLBOXES пакеты прикладных программ;
• SIMULINK система для имитационного моделирования проектов, представленных в виде композиции функциональных блоков, источников сигналов, приемников и измерительных средств;
• МАТЛАБ EXTANTIONS набор программных средств, позволяющий упростить и ускорить реализацию разработок, выполненных с использованием МАТЛАБ (это компилятор, библиотека функций на языке С и С++ и др.);
• GUI графический интерфейс пользователя – средство, позволяющее в предметной области для наиболее часто встречающихся задач одного плана (расчет фильтров, спектральный анализ, вейвлет-анализ и др.) создать инструмент анализа, расчета, проектирования, максимально приближенный к практическим потребностям инженера и требующий для освоения минимальных интеллектуальных и временных затрат.

По системе МАТЛАБ написано много книг (см. www.mathworks.com и библиографию к заметке), только на русском языке около 10. Упомянутые издания можно разделить на несколько групп:

• книги, посвященные собственно системе МАТЛАБ или отдельным ее частям;
• книги, посвященные организации и проведению учебного процесса по различным аспектам системы;
• книги прикладного или теоретического характера в конкретных предметных областях, использующие МАТЛАБ как инструмент для решения примеров и задач и средство организации иллюстраций.

В качестве предметной области, для которой строятся содержательные примеры, использованы приложения, имеющие дело с обработкой сигналов. А в качестве предмета обучения выбраны два типа инструментов: МАТЛАБ-SIMULINK и GRAPHICAL USER INTERFACE (GUI). Первый обеспечивает имитационное моделирование сложных систем в разнообразных режимах, а второй графический интерфейс пользователя предназначен для решения задач анализа и синтеза расчета разнообразных объектов в режиме, максимально удобном и наглядном для пользователя.

Во многих (хотя далеко не во всех) случаях именно с помощью этого инструментария инженер либо студент может решить часто встречающиеся задачи с минимальными затратами времени и сил на обучение и прийти к цели кротчайшим путем. Именно это обстоятельство способно увлечь, сформировать неформальный интерес и в последующем побудить читателя к основательному знакомству с МАТЛАБ.

Введение

Simulink является мощным средством решения таких задач для разных предметных областей и, может быть, в первую очередь, для задач в области цифровой обработки сигналов. Использование Simulink во многих случаях исключает утомительные и трудоемкие этапы составления и отладки программ, позволяя сосредоточить основные усилия непосредственно на решении "своих" предметно-ориентированных задач. Инженеру или студенту нужно освоить правила использования готовых функциональных блоков, из которых, как из конструктора, составляется модель проектируемого устройства, а также, и это следует особо подчеркнуть, "испытательный стенд", то есть вся необходимая инфраструктура, включающая источники сигналов, измерительные приборы и средства наблюдения за процессами и характеристиками процессов. При этом гарантируется высокое качество "строительного материала", в создании которого использованы опыт и знания ведущих специалистов.

Итак, Simulink – это интерактивная графическая программа, управляемая мышью, которая позволяет моделировать динамические системы на уровне структурных и функциональных схем. Библиотеки Simulink содержат большое количество разнообразных функциональных блоков, которые отображаются на экране в виде пиктограмм.

Построение модели сводится к перемещению с помощью мыши необходимых блоков из библиотек Simulink в окно создаваемой модели и соединению этих блоков между собой. Работая с программой Simulink, можно создавать модели линейных и нелинейных, аналоговых, дискретных и смешанных (аналогово-дискретных) цепей и систем, изменять параметры блоков непосредственно во время процесса моделирования и сразу же наблюдать реакцию моделируемой системы. Все это делает работу с Simulink одинаково привлекательной как для начинающих пользователей, так и для опытных специалистов. В пакет MATLAB 5.3 входит подробное описание программы Simulink, которое содержится в файле sl_using.pdf. Отметим также вышедшие недавно книги [1,2], содержащие основные сведения о Simulink и примеры моделей динамических систем.

В настоящей работе описывается процесс построения простой модели аналого-цифрового преобразователя (АЦП), а также рассматриваются эффекты, связанные с аналого-цифровым преобразованием. В первой части приводятся состав и краткое описание модели, процесс ее построения, а также процедура компоновки модели. Во второй части приведены процесс построения модели, необходимые сведения о входящих в нее функциональных блоках и результаты моделирования, а также дополнительные возможности по использованию модели.