Локальный экстремум функции нескольких переменных

Пусть 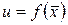определена на 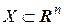, и .

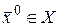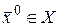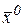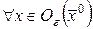Определение 23. Внутренняя точка называется точкой строгого локального максимума функции , если существует такая окрестность точки , что и 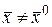, выполняется неравенство .

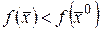Если 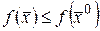, то точка нестрогого локального максимума.

Если 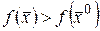, то точка строгого локального минимума.

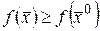Если , то точка нестрогого локального минимума.

Точки локального максимума и минимума называются точками экстремума функции .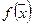

Теорема 12 (необходимое условие экстремума). Если функция 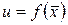дифференцируема в точке и имеет в этой точке локальный (нестрогий) экстремум, то выполняются

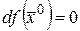и 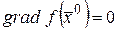. (35)

ƒ Так как по определению имеем

, ,

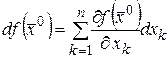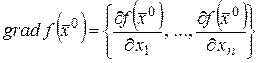то нужно доказать, что для 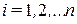выполняются равенства 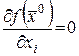. Рассмотрим функцию 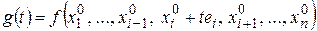, у которой все переменные зафиксированы, кроме 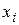, а 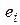– направляющий вектор оси 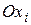. Тогда, так как в точке имеет экстремум, то 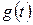в точке 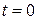тоже имеет экстремум, как функции одной переменной. Отсюда согласно теореме Ферма 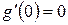. Таким образом, из определения частной производной получаем:

, <

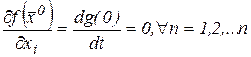Замечание. Условия (35) является необходимыми, но не достаточными. Например, функция 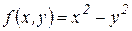дифференцируемая в точке 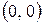и

, , , ,

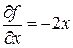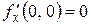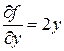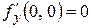но экстремума в точке 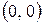нет (рис. 4), так как в любой окрестности точки (0, 0) 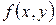принимает как положительное, так и отрицательное значения.

Определение 24. Точка 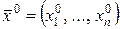называется стационарной точкой функции , если выполняется условие (35).

Стационарная точка называется регулярной, если в этой точке существует второй дифференциал 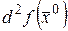, (т.е. существуют все частные производные второго порядка) и он является невырожденной квадратичной формой переменных .

	Рис.4

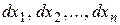Так как матрица квадратичной формы 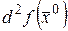есть матрица Гессе 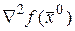, то невырожденность квадратичной формы означает, что определитель матрицы Гессе 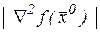, который называется гессиан, не равен нулю.

Теорема 13 (достаточное условие экстремума). Пусть функция 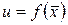дважды дифференцируемой в окрестности точки , где – стационарная точка, а второй дифференциал 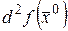в точке есть невырожденная квадратичная форма переменных 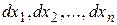. Тогда:

если 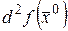– положительная определенная квадратичная форма, то точка локального минимума;

если 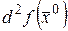– отрицательная квадратичная форма, то – точка максимума;

если 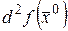– знакопеременная квадратичная форма, то не является точкой экстремума.

ƒ Так как – стационарная точка, то из теоремы 12 следует

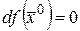и .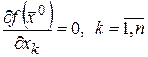

Запишем формулу Тейлора для случая m=2 с остаточным членом в форме Пеано

,

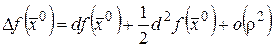где , , .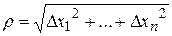

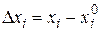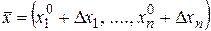Тогда формулу Тейлора можно переписать в виде

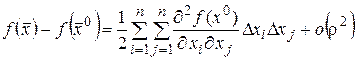. (36)

Короткое (упрощенное) доказательство. Пусть второй дифференциал является отрицательно определенной квадратичной формой (функцией) в точке . Тогда, при любых значениях 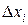в окрестности точки , эта функция принимает отрицательное значение, т.е. 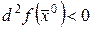и из (36) следует, что 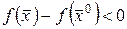. Отсюда следует, что - точка максимума. Аналогично, остальное доказательство.

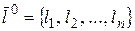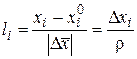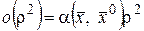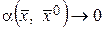Подробное доказательство. Рассмотрим единичный вектор сонаправленный с вектором, соединяющим и : , . Обозначим , где при 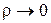. Тогда

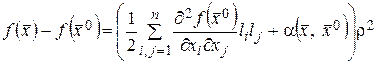
или

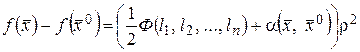. (37)

Пусть второй дифференциал 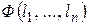есть положительно определенная квадратичная форма. Квадратичная форма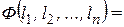 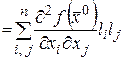задана на единичной сфере 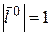, которая есть ограниченное замкнутое множество. По теореме Вейерштрасса функция n переменных 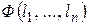достигает своего наименьшего значения на этом множестве, т.е. достигает нижней гран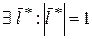и: и .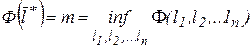

Ясно, что 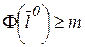для произвольного значения 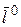. Тогда из положительно определенности квадратичной формы и условия 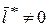, следует, что 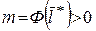. Тогда

, .

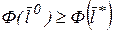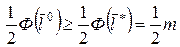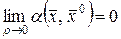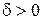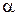Так как , то существует , что в 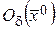можно сделать не более любого наперед заданного числа, например 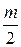, т.е.

, .

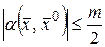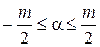Из полученного соотношения и формулы (37) следует, что

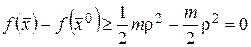, т.к.

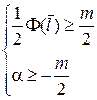
а откуда 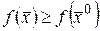, тогда – точка минимума.

Если второй дифференциал функции есть отрицательно определенная квадратичная форма, то второй дифференциал функции 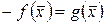в стационарной точке будет положительно определенной квадратичной формой. Тогда – точка локального максимума функции .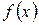

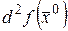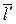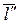Пусть – знакопеременная квадратичная форма. Тогда существуют такие единичные векторы и , что

,

.

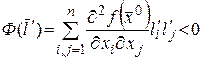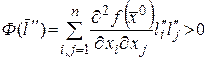По формуле (37) имеем

,

,

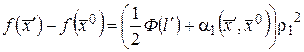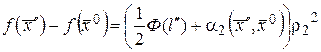где 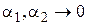при 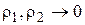. Так как 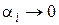, то можно выбрать их сколь угодно малыми, так что слагаемые в скобках будут иметь фиксированные знаки. Тогда существует 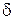-окрестность точки такая, что для 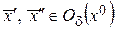выполняются неравенства

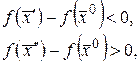
т.е. в любой сколько угодно малой окрестности точки не выполняется определение экстремума. ■

Следствие. Пусть 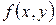дважды дифференцируемая функция в окрестности стационарной точки 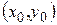, тогда:

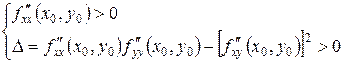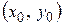если , то – точка минимума функции ;

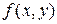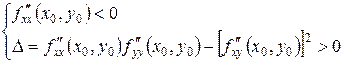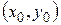если , то – точка максимума функции ;

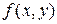если 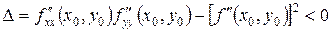, то в точке 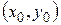экстремума нет.

Справедливость следствия следует из критерия Сильвестра знакоопределенности квадратичных форм и теоремы 13. Здесь матрица Гессе имеет вид:

,

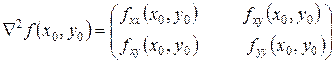а гессиан есть определитель второго порядка .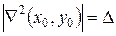

Пример.Для функции 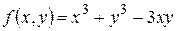найти точки экстремума или показать, что их нет.

Решение. Определим стационарные точки:

,

.

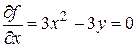Решая систему, получаем две точк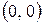и и 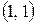. Найдем матрицу Гессе:

.

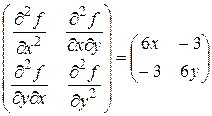Используя следствие, для точки 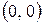получаем

,

.

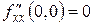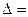
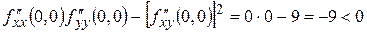Следовательно, в точке 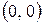экстремума нет.

Для точки 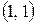получаем

,

.

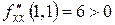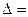
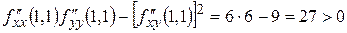Следовательно, 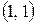точка локального минимума.