От перестановки слагаемых сумма не изменяется.

Свойство перестановки слагаемых (переместительное свойство сложения) используется в 1 классе при знакомстве с вычислительными приемами вида а+5, а+6, а+7, а+8 и а+9.

В этих случаях второе слагаемое больше первого (поскольку рассматриваются случаи сложения в пределах 10). Применение при вычислениях перестановки слагаемых позволяет свести все эти случаи к ранее изученным.

Например: 2+8=8+2=10.

Перестановка слагаемых может рассматриваться как прием вычислений.

Этот вычислительный прием облегчает вычислительную деятельность и является общим приемом вычислений при сложении любых чисел.

Например: 12+346=346+12=358

Прием перестановки слагаемых позволяет составитькраткую таблицу сложения в пределах 10:

2+2=4

3+2=5

4+2=6 3+3=6

5+2=7 4+3=7

6+2=8 5+3=8 4+4=8

7+2=9 6+3=9 5+4=9

8+2=10 7+3=10 6+4=10

С учетом свойства перестановки слагаемых данная таблица включает все случаи сложения в пределах 10. Таблица содержит 15 случаев и, безусловно, ее заучивание для ребенка намного более легкая задача, чем заучивание полной таблицы.

Данная таблица появляется значительно позднее, чем начинается заучивание таблиц (для случаев а±1, а±2, а±3, а± 4 ) сложения и вычитания в пределах 10, поэтому не выполняет своей облегчающей вычисления задачи. На данный момент дети уже заучивали 42 случая предыдущих таблиц, и поэтому все случаи часто смешиваются. В связи с этим, некоторые альтернативные учебники (например, учебник Н.Б. Истоминой) сначала знакомят детей со сложением, его свойствами и таблицей сложения, а после того, как эти таблицы ребенком усваиваются, знакомят первоклассника с действием вычитания и таблицу вычитания рассматривают отдельно от таблицы сложения.

Случаи вида «вычесть 5, 6, 7, 8, 9», символически обозначаемые в учебниках

-5, -6, -7, -8, -9, являются вычислительными приемами, основанными на составе однозначных чисел и взаимосвязи между суммой и слагаемыми.

С правилом взаимосвязи суммы и слагаемых дети знакомились ранее (см. выше). Состав чисел изучался в разделе «Нумерация в пределах 10».

Используя эти знания, дети осваивают прием вычитания чисел больше5:

8-5=3 7-6=1 10-7=3

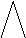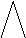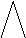3 5 6 1 7 3

(8 – это 3 и 5; 8 без 5 – это 3.)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ С НУЛЕМ

Основное свойство нуля:

Прибавление и вычитание нуля результата не меняет.

В общем виде это свойство можно записать так: а ± 0 = а и 0± а = а.

ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ БЕЗ СКОБОК

Порядок действий в выражениях без скобок в первом классе определяется следующим образом:

В выражении, содержащем сложение и вычитание, или несколько знаков сложения, или несколько знаков вычитания, действия выполняются по порядку слева направо.

Это правило не содержится в учебнике, учитель знакомит с ним детей в процессе решения соответствующих примеров. Например:

Вычисли: 3+6-7=…; 8-9+4=…; 7-3-2=…; 5+6+3=…

При вычислении этих примеров детям в 1 классе не разрешается пользоваться правилом группировки слагаемых, являющимся приемом рациональных вычислений.

Это правило появляется только во втором классе при изучении приемов вычислений в пределах 100, где детям сообщается: