Формулы для вычисления параметров функций для указанных ниже распределений

4.1 Равномерный закон распределения вероятностей

Непрерывная случайная величина X называется распределенной равномерно на отрезке [a,b], если её плотность распределения вероятностей постоянна на данном отрезке:

.

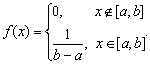Функция распределения в этом случае примет вид:

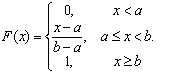.Здесь нужно описать моменты для функции Распределения.

Числовые характеристики случайной величины X равномерно распределенной на интервале [a,b]:

1. Математическое ожидание по формуле:

.

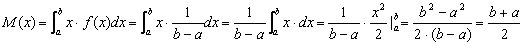2. Дисперсия по формуле:

.

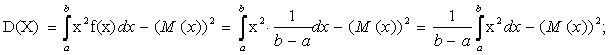
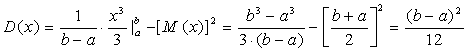3. Среднее квадратическое отклонение – s(Х) по формуле:

+

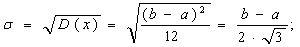http://edu.tltsu.ru/er/book_view.php?book_id=1cee&page_id=19506

4.2 Экспоненциальный закон распределения вероятностей

Непрерывная случайная величина Х имеет показательный(экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид

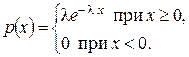
Функция распределения случайной величины, распределенной по показательному закону, равна

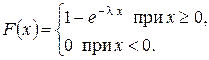
Кривая распределения р(х) и график функции распределения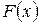

Для случайной величины, распределенной по показательному закону

; .

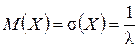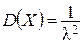Вероятность попадания в интервал 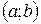непрерывной случайной величины Х, распределенной по показательному закону

.

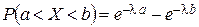4.3 Закон Пуассона

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии 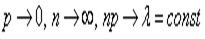закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность 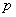события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения:

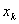			…..	k	…..
			…..		…..

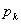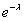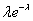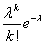Вероятности вычисляются по формуле Пуассона: .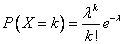

Числовые характеристики: , ,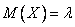

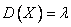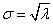
Разные многоугольники распределения при .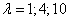

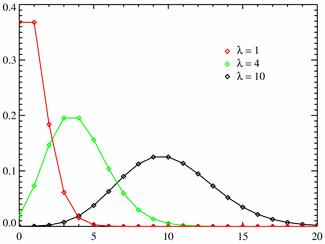
Закон распределения Пуассона - вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Чему равно k в этих графика[?

4.4 Нормальный закон распределения или распределение Гаусса

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения:

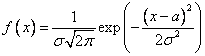
Числовые характеристики: , ,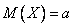

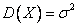Пример плотности распределения:

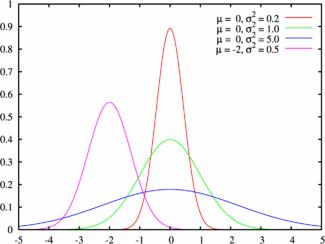
Что такое µ на этих графиках?

Нормальный закон распределения случайной величины с параметрам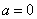и и 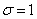называется стандартным или нормированным, а соответствующая нормальная кривая - стандартной или нормированной.

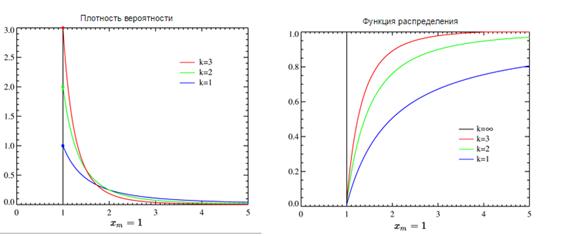
4.5 Закон Парето

Пусть случайная величина {\displaystyle X}X такова, что её распределение задаётся равенством:

{\displaystyle F_{X}(x)=P(X<x)=1-\left({\frac {x_{m}}{x}}\right)^{k},\;\forall x\geq x_{m}} ,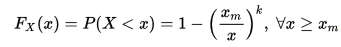

где x_m,k>0{\displaystyle x_{m},k>0}. Тогда говорят, что {\displaystyle X}X имеет распределение Парето с параметрами {\displaystyle x_{m}}x_m и {\displaystyle k}k. Плотность распределения Парето имеет вид:

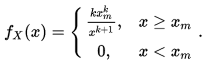
Моменты случайной величины, имеющей распределение Парето, задаются формулой:

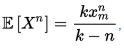
откуда в частности:

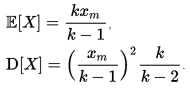Что означает к=1? К=1 нет в формуле, не понял вашего вопроса Прочитайте не в Википедии значение всех коэффициентов в этом распределении!

Графики функции для разных параметров распределения=? ниже