Обобщенный метод наименьших квадратов. (ОМНК).
При гетероскедастичности и автокорреляции остатков нельзя использовать традиционный МНК, его необходимо заменять обобщенным МНК.
Обобщенный МНК применятся к преобразованным данным и позволяет получать несмещенные и эффективные оценки.
Рассмотрим сначала коррекцию гетероскедастичности.
Как и раньше, предполагается, что математическое ожидание остатков равно 0, а дисперсия их пропорциональная некоторой величине К, т.е.будем полагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, будет пропорциональна величине 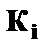 , т.е.
, т.е.
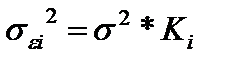 ,
,
Где 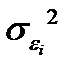 - дисперсия ошибки при конкретном i-м значении фактора;
- дисперсия ошибки при конкретном i-м значении фактора;
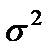 - постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
- постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
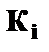 - коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
- коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
При этом предполагается, что 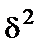 неизвестна, а в отношении величины К выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
неизвестна, а в отношении величины К выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде для уравнения
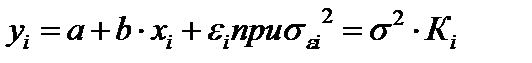

Модель примет вид: 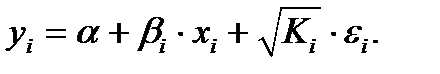
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе i-го наблюдения на 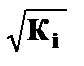 . Тогда дисперсия остатков будет величиной постоянной, т.е.
. Тогда дисперсия остатков будет величиной постоянной, т.е. 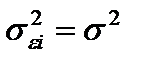 . Иными словами, от регрессии у по x мы перейдем к регрессии на новых переменных:
. Иными словами, от регрессии у по x мы перейдем к регрессии на новых переменных: 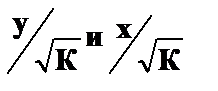 .
.
Уравнение регрессии примет вид:
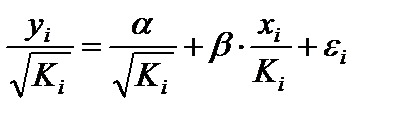
Исходные данные для данного уравнения будут иметь вид:
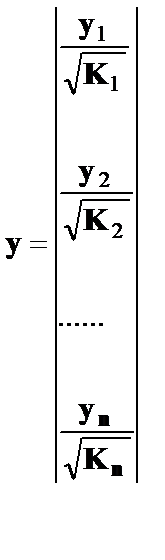
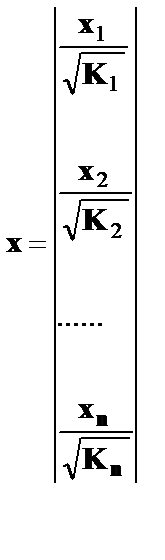
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными, представляет собой взвешенную регрессию, в которой переменные у и x взяты с весами 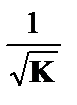 .
.
Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отключений вида:
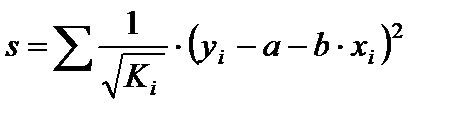
Соответственно получим следующую систему нормальных уравнений:
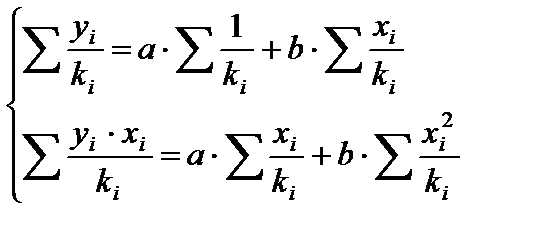
Если преобразованные переменные x и у взять в отклонениях от средних уровней, то коэффициент регрессии b можно определить как
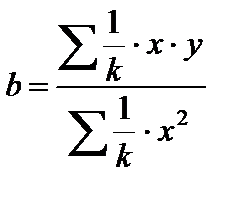
При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии b определяется по формуле
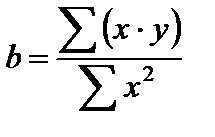
Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.
Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Предположим, что рассматривается модель вида
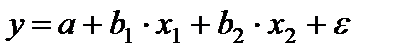 ,
,
Для которой дисперсия остаточных величин оказалась пропорциональна 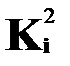 .
. 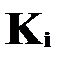 - представляет собой коэффициент пропорциональности, принимающий различные значения для соответствующих
- представляет собой коэффициент пропорциональности, принимающий различные значения для соответствующих 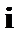 значений факторов
значений факторов 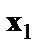 и
и 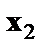 . Ввиду того, что
. Ввиду того, что
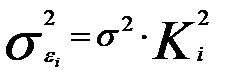 ,
,
Рассматриваемая модель примет вид
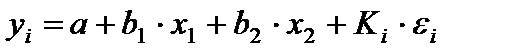 ,
,
Где ошибки гетероскедастичны.
Для того чтобы получить уравнение, где остатки 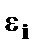 гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности К. уравнение с преобразованными переменными составит:
гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности К. уравнение с преобразованными переменными составит:
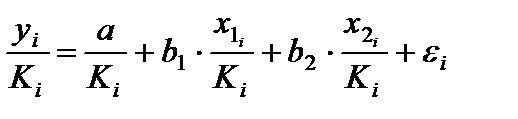
Это уравнение не содержит свободного члена. Вместе с тем , найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели:
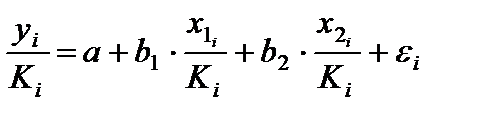
Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности 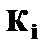 . В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки
. В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки 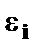 пропорциональны значениям фактора. Так, если в уравнении
пропорциональны значениям фактора. Так, если в уравнении 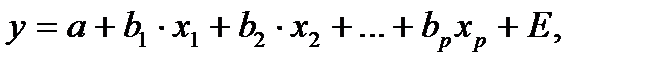
предположить, что 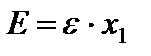 , т.е.
, т.е. 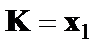 и
и 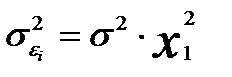 , то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:
, то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:
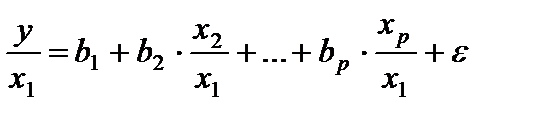
Если предположить, что ошибки пропорциональны 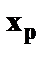 , то модель примет вид:
, то модель примет вид:
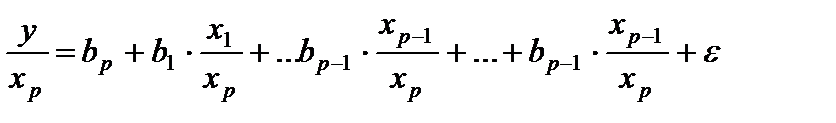
Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший все, чем с первоначальными переменными. Вместе с тем следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
Пример.
Пусть у – издержки производства, 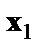 - объем продукции,
- объем продукции, 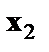 - основные производственные фонды,
- основные производственные фонды, 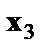 - численность работников, тогда уравнение
- численность работников, тогда уравнение
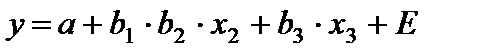
Является моделью издержек производства с объемными факторами. Предполагая, что 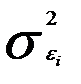 пропорциональна квадрату численности работников
пропорциональна квадрату численности работников 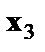 ,мы получим в качестве результативного признака затраты на одного работника (у/
,мы получим в качестве результативного признака затраты на одного работника (у/ 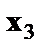 ), а в качестве факторов следующие показатели: производительность труда
), а в качестве факторов следующие показатели: производительность труда 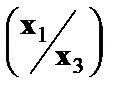 и фондовооруженность труда
и фондовооруженность труда 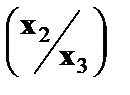 . Соответственно трансформированная модель примет вид:
. Соответственно трансформированная модель примет вид:
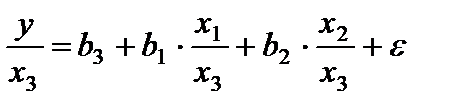
Где параметры 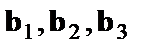 численно не совпадают с аналогичными параметрами предыдущей модели. Кроме того, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на одного работника; с изменением производительности труда на единицу при неизменном уровне фондовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.
численно не совпадают с аналогичными параметрами предыдущей модели. Кроме того, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на одного работника; с изменением производительности труда на единицу при неизменном уровне фондовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.
Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, 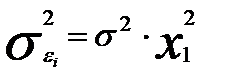 , можно перейти к уравнению регрессии вида:
, можно перейти к уравнению регрессии вида:
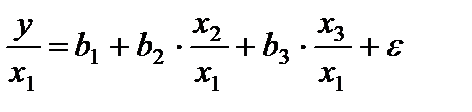
В нем новые переменные: 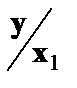 - затраты на единицу (или на 1 руб. продукции),
- затраты на единицу (или на 1 руб. продукции), 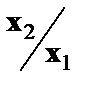 - фондоемкость продукции,
- фондоемкость продукции, 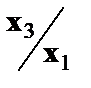 - трудоемкость продукции.
- трудоемкость продукции.
Гипотеза о пропорциональности остатков величине фактора может иметь реальное основание: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие предприятия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остаточных величин.
При наличии одной объясняющей переменной гипотеза 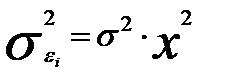 трансформирует линейное уравнение
трансформирует линейное уравнение 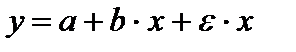
в уравнение 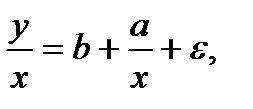
в котором параметры а и b поменялись местами, константа стала коэффициентом наклона линии регрессии – свободным членом.
Пример. Рассматривая зависимость сбережений у от дохода x, по первоначальным данным было получено уравнение регрессии 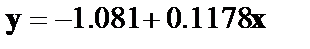
Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных:
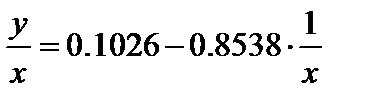
Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т. е. 0,1178 и 0,1026 – оценки параметра bзависимости сбережений от дохода.
Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки. Он представляет собой наиболее простой случай учета гетероскедастичности в регрессионных моделях с помощью обобщенного МНК. Процесс перехода к относительным величинам может быть осложнен выдвижением иных гипотез о пропорциональности ошибок относительно включенных в модель факторов. Например, 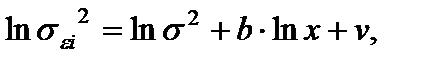 т. е. рассматривается характер взаимосвязи
т. е. рассматривается характер взаимосвязи 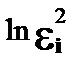 от
от 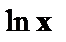 . Использование той иной гипотезы предполагает специальные исследования остаточных величин для соответствующих регрессионных моделей. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией.
. Использование той иной гипотезы предполагает специальные исследования остаточных величин для соответствующих регрессионных моделей. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией.
Регрессионные модели с переменной структурой (фиктивные переменные). Фиктивные переменные: общий случай. Множественные совокупности фиктивных переменных. Фиктивные переменные для коэффициентов наклона.
До сих пор в качестве факторов рассматривались экономические принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В отечественной литературе можно встретить термин «структурные переменные».
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:
Y=a + b · x + ε,
Где у – количество потребляемого кофе;
X – цена.
Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 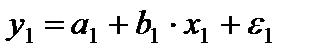 и женского пола:
и женского пола: 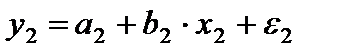 .
.
Различия в потреблении кофе проявятся в различии средних 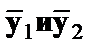 . Вместе с тем сила влияния x на у может быть одинаковой, т.е.
. Вместе с тем сила влияния x на у может быть одинаковой, т.е. 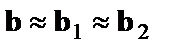 . в этом случае возможно построение общего уравнения регрессии с включением в него фактора«пол» в виде фиктивной переменной. Объединяя уравнения
. в этом случае возможно построение общего уравнения регрессии с включением в него фактора«пол» в виде фиктивной переменной. Объединяя уравнения 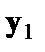 и
и 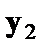 и вводя фиктивные переменные, можно прийти к следующему выражению:
и вводя фиктивные переменные, можно прийти к следующему выражению:
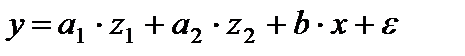
Где 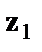 и
и 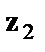 -фиктивные переменные, принимающие значения:
-фиктивные переменные, принимающие значения:
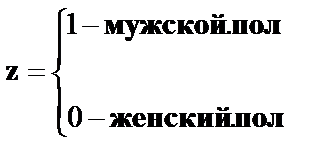
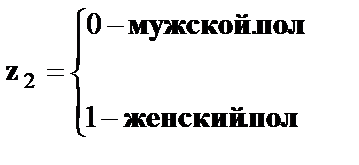
В общем уравнении регрессии зависимая переменная у рассматривается как функция не только цены x, но и пола 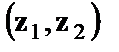 . Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом, когда
. Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом, когда 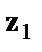 =1,то
=1,то 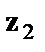 =0 и, наоборот, при
=0 и, наоборот, при 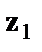 =0 переменная
=0 переменная 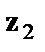 =1.
=1.
Для лиц мужского пола, когда 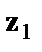 =1 и
=1 и 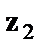 =0, объединенное уравнение регрессии составит:
=0, объединенное уравнение регрессии составит: 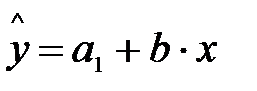 , а для лиц женского пола
, а для лиц женского пола 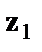 =0 и
=0 и 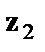 =1,
=1, 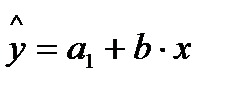 . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии:
. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: 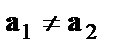 . Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
Следует иметь в виду, что при введении фиктивных переменных 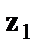 и
и 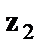 в модель
в модель 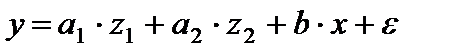 применение МНК для оценивания параметров
применение МНК для оценивания параметров 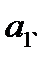 и
и 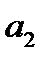 ,приведет к вырожденной матрице исходных данных, а, следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид:
,приведет к вырожденной матрице исходных данных, а, следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид:
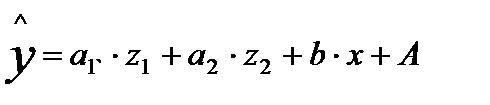
Предполагая при параметре А независимую переменную, равную 1, имеем матрицу исходных данных:
1 1 0 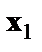 1 1 0 1 1 0 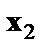 1 0 1 1 0 1 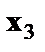 1 1 0 1 1 0 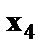 …………. 1 0 1 …………. 1 0 1 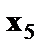 |
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям
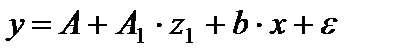
Или
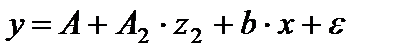
Т.е. каждое уравнение включает только одну фиктивную переменную 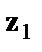 или
или 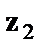 .
.
Предположим, что определено уравнение
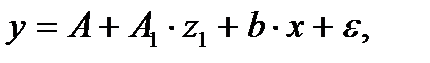
где 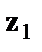 - принимает значения 1 для мужчин и 0 для женщин.
- принимает значения 1 для мужчин и 0 для женщин.
Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
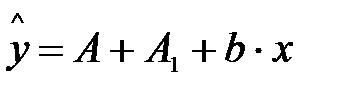
Для женщин соответствующие значения получим из уравнения
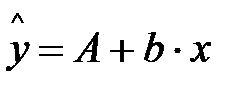
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: А- для женщин и 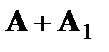 - для мужчин.
- для мужчин.
Пример.Проанализируем зависимость цены двухкомнатнойквартиры от ее полезной площади. При этом в модель могут быть ведены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный.
При использовании трех категорий домов вводятся две фиктивные переменные: 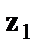 и
и 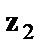 . Пусть переменная
. Пусть переменная 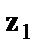 принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная
принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная 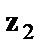 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные
принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные 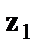 и
и 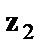 принимает значения 0 для домов типа «хрущевки».
принимает значения 0 для домов типа «хрущевки».
Предположим, что уравнение регрессии с фиктивными переменными составило:
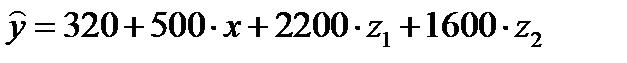
Частые уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид:
v «хрущевки» - 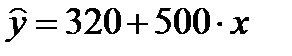 ;
;
v Панельные - 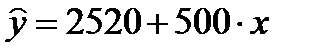 ;
;
v Кирпичные - 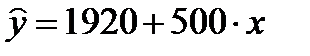 ;
;
Параметры при фиктивных переменных 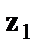 и
и 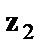 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых
представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых 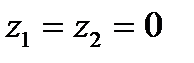 . параметр при
. параметр при 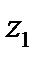 =2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долл. США выше, чем в «хрущевки». Соответственно параметр при
=2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долл. США выше, чем в «хрущевки». Соответственно параметр при 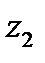 показывает, что в кирпичных домах цена выше в среднем на 1600 долл. При неизменной величине полезной площади по сравнению с указанным типом домов.
показывает, что в кирпичных домах цена выше в среднем на 1600 долл. При неизменной величине полезной площади по сравнению с указанным типом домов.
В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т.е. двух и более качественных факторов, каждый из которых может несколько градаций. Например, при изучении потребления некоторого товара наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.) учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной.
Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак играет роль результата. Подобного вида модели применяются, например, обработке данных социологических опросов. В качестве зависимой переменной у рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет». Поэтому зависимая переменная имеет два значения: 1,когда имеет место ответ «да», и 0 – во всех остальных случаях. Модель такой зависимой переменной имеет вид:
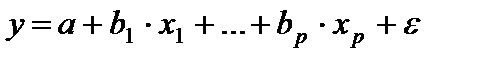
Модель является вероятностной линейной моделью. В ней у принимает значения 1 и 0, которым соответствуют вероятности p и 1-p. Поэтому при решении модели находят оценку условной вероятности события у при фиксированных значениях x.
Среди моделей с фиктивными переменными наибольшими прогностическими возможностями обладают модели, в которых зависимая переменная у рассматривается как функция ряда экономических факторов 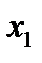 и фиктивных переменных
и фиктивных переменных 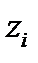 . Последние обычно отражают различия в формировании результативного признака по отдельным группам единиц совокупности, т.е. в результате неоднородной структуры пространственного или временного характера.
. Последние обычно отражают различия в формировании результативного признака по отдельным группам единиц совокупности, т.е. в результате неоднородной структуры пространственного или временного характера.
Проверка гипотез с помощью t-критерия показывает, что все коэффициенты при фиктивных переменных значимо отличаются от нуля.
Может потребоваться включить в уравнение регрессии более одной совокупности фиктивных переменных. Это часто встречается при работе со статистическими данными перекрестных выборок, когда могут быть собраны данные по ряду как качественных, так и количественных переменных. При этом если четко определены рамки работы, то расширение использования фиктивных переменных не представляет проблемы.
Библиографический список
Основная литература
1. Елисеева, И.И. Эконометрика: учебник для вузов /И.И. Елисеева [и др.]; под ред. И.И. Елисеевой.— М.: Проспект, 2013 .— 288с.
2. Кремер Н.Ш. Эконометрика [Электронный ресурс]: учебник / Кремер Н.Ш., Путко Б.А. —Электрон. текстовые данные. — М.: ЮНИТИ-ДАНА, 2012, — 328 с.— Режим доступа: http// www. iprbookshop.ru /8594. — ЭБС «IPRbooks», по паролю
Дополнительная литература
1. Елисеева, И.И. Эконометрика: учебник для вузов /И.И. Елисеева [и др.]; под ред. И.И. Елисеевой.— М.: Проспект, 2009 .— 288с. (1 экз.)
2. Елисеева, И.И. Эконометрика: учебник для вузов / И.И. Елисеева [и др.]; под ред. И.И. Елисеевой .— 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2008 .— 576с. (12 экз.)
3. Елисеева И.И. Практикум по эконометрике: учебное пособие для экономических вузов./И.И. Елисеева [и др.]; под ред. И.И. Елисеевой .— 2-е изд., перераб. и доп. — М. : Финансы и статистика, 2008 .— 344с.+1 опт. диск (CD-ROM). (8 экз.)
4. Эконометрика [Электронный ресурс]: учебно-мультимедийный компьютерный курс .— Multimedia (110MB) .— М. : Диполь, 2007 .— 1 опт. диск. (CD ROM) .— (Вузовская серия).
5. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов. – 2-е изд., перераб. и доп. –М.: ЮНИТИ-ДАНА, 2006, - 573с.
6. Колемаев, В.А.Государственный университет управления Эконометрика: учебник для вузов / В.А.Колемаев; Гос. ун-т управления. — М.: Инфра-М, 2006 .— 160с.
7. Кочетыгов, А.А. ТулГУ Эконометрика: учебное пособие / А.А.Кочетыгов, Л.А.Толоконников; ТулГУ .— Тула : Изд-во ТулГУ, 2006 .— 320с.
8. Магнус, Я.Р. Эконометрика: Начальный курс: учебник для вузов / Я.Р.Магнус, П.К.Катышев, А.А.Пересецкий .— 7-е изд., испр. — М.: Дело, 2005. — 576с.
