Исследование остатков величин регрессии.

Прежде всего, проверяется случайный характер остатков 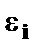. – первая предпосылка МНК.

С этой целью стоится график зависимости остатков. От теоретических значений результативного признака (рис. 3.1).

[1]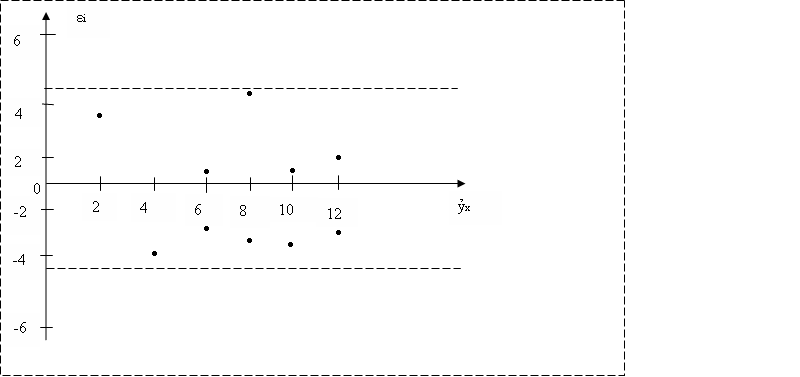

Рис.3.1.Зависимость случайных остатков 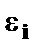от теоретических значений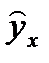

Если на графике получена горизонтальная полоса, то остатки 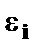представляют собой случайные величины и МНК оправдан, теоретические значения 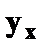хорошо аппроксимируют фактические значения у.

Возможны следующие случаи: если 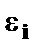зависит от 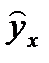то:

v Остатки 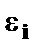не случайны (рис. 3.2а);

v Остатки 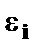не имеют постоянной дисперсии (рис. 3.2в);

v Остатки 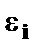носят систематический характер (рис. 3.2б), в данном случае отрицательные значения 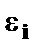соответствуют низким значениям 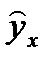, а положительные – высоким значениями.

В случаях а), б), в), (рис. 3.2) необходимо либо применять другую функцию, либо вводить дополнительную информацию и вновь строить уравнение регрессии до тех пор, пока остатки 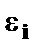не будут случайными величинами.

Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что Σ(у- 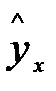) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых. Для моделей, нелинейных по оцениваемым параметрам и приводимых к линейному виду логарифмированием, средняя ошибка равна нулю для логарифмов исходных данных. Так для модели вида , .

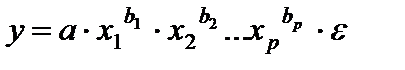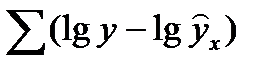
Вместе с тем несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин x, что исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков 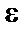от теоретических

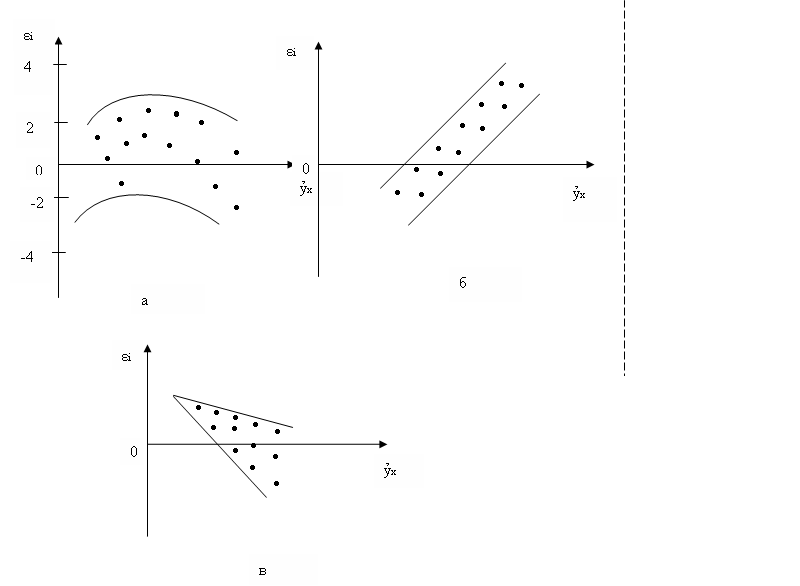
Рис.3.2. Зависимость случайных остатков 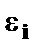от теоретических значений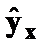

значений результативного признака 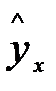строится график зависимости случайных остатков e от факторов, включенных в регрессию x_i (рис.3.3).

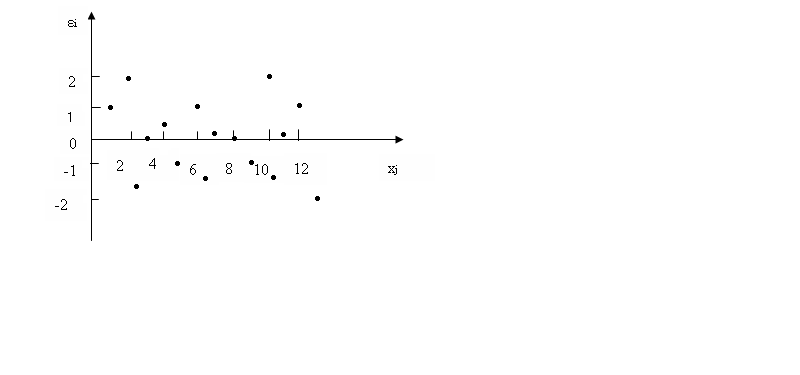
Рис.3.3. Зависимость случайных остатков от величины фактора x_j

Если остатки расположены в виде горизонтальной полосы (см. рис.3.3), то они независимы от значений x_j. Если же график показывает наличие зависимости e_i и x_j , то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора x_j. Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от x_j, например x_j², или преобразовать значения у. скопление точек в определенных участках значений фактора x_j говорит о наличии систематической погрешности модели.

Корреляция случайных остатков с факторными признаками позволяет проводить корректировку модели, в частности использовать кусочно-линейные модели.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки МНК.

Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.