Теория одностороннего замера на линии с двусторонним питанием

Первым из приборов одностороннего замера, работающих на дистанционном принципе, был прибор ФИС, выпускавшийся в небольших количествах в начале 80-х годов. Проблема устранения влияния переходного сопротивления в нем решалась тем, что прибор реагировал на реактивную составляющую сопротивления "на зажимах": X = Im ( U_ф / (I_Ф + KI₀ ). Непосредственно из рис.15 можно заключить, что влияние переходного сопротивления исключалось только либо на ненагруженных линиях, либо на линиях с односторонним питанием. Для расширения области применения делались попытки осуществлять замер в режиме каскадного включения линии при неуспешном АПВ. Однако это не являлось полноценным решением проблемы.

Положение изменилось только после появления разработки Рижского политехнического института (А.С. Саухатас) - прибора МФИ, реализовавшего принципы, разработанные в [6]. Рассмотрим теоретические основы действия прибора.

Согласно формулам (15) и (16) и рисунку 15, замер дистанционного устройства Z складывается из сопротивления линии до места КЗ Z_1K и вектора ΔZ. Длины двух указанных векторов неизвестны. Но известны их направления: вектор Z_1K направлен вдоль оси сопротивления линии; направление вектора ΔZ можно найти почти точно. Для пояснения обратимся к формуле (15) для случая однофазного короткого замыкания. Если считать переходное сопротивление чисто активным, то направление ΔZ определяется соотношением токов I_0K и (I_Ф + +KI₀ ). Токи I_Ф и I₀ можно измерить на данном конце линии. Ток I_0K существует только в месте замыкания. Однако к этому току весьма близок по фазе ток нулевой последовательности I₀, поскольку токораспределение по схеме нулевой последовательности мало меняет фазу токов в отдельных элементах. Для угла, под которым вектор ΔZ наклонен к горизонтали, можно написать формулу:

arg ΔZ = arg[I_0K/( I_Ф+ KI₀ )]= arg[I₀ /( I_Ф+ KI₀ )] –arg[I₀ / I_0K]=α - β,

где α = arg[I₀ /( I_Ф+ KI₀), β = arg[I₀ / I_0K] (17)

Угол α может быть сосчитан по измерениям на одном конце линии. Угол β очень мал, им иногда можно пренебречь.

Графическое решение задачи определения Z_1K пояснено на рис.17. На комплексной плоскости построены вектор Z и ось сопротивления линии. Затем через точку конца вектора ΔZ проведена прямая под углом α–β κ горизонтали. Пересечение прямой с осью сопротивления дает точку конца вектора Z_1K, в частности, реактивное сопротивление до места КЗ - X_1K

Возможно получение аналитической формулы для X_1K путем решения треугольника. Согласно [6] расчетная формула имеет вид:

X - R tg(α–β)

X_1K = ———————— tg ф_Л, (18)

tg ф_Л – tg(α–β)

где tg ф_Л = X_Л/R_Л, X и R – составляющие вектора Z.

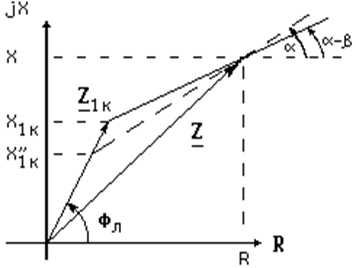Рис.17 К пояснению принципа одностороннего ОМКЗ

В формуле известно все, кроме угла β, который нельзя измерить на одном конце линии. Приближенное решение предполагает пренебрежение углом и. Тогда аналитическая формула приобретает вид:

X - R tg(α)

X_1K″ = ———————— tg ф_Л, (19)

tg ф_Л – tg(α)

Графическая интерпретация приближенного решения показана на рис.17: если через конец вектора Z провести прямую не под углом (α–β), а под углом α, то получим не точное решение X_1K, а приближенное X_1K″. Следовательно, односторонний замер оказался возможным потому, что направление тока I_0K приняли совпадающим с направлением тока I₀.

В[7] введено понятие опорного тока - тока, близкого по фазе к току в переходном сопротивлении. Для однофазного КЗ это либо ток нулевой последовательности I₀ , либо ток обратной последовательности I₂ , либо аварийная составляющая тока прямой последовательности I₁–I^(Н) , либо аварийная составляющая тока фазы I_Ф-I^(Н) . Для использования аварийных составляющих необходимо знание тока предшествующего нагрузочного режима I^(Н). Для этого прибор должен запоминать значение предшествующего тока, что в принципе возможно. Еще проще решается вопрос при использовании для расчета данных от цифровых осциллографов - осциллографы всегда записывают не только токи КЗ, но и несколько периодов величин предшествующего режима. Использование аварийных составляющих возможно в предположении, что за время КЗ угол между ЭДС систем не успел значительно измениться - иначе в аварийную составляющую войдет и часть тока прямой последовательности, что приведет к погрешностям.

Из формулы (16) следует, что при замыкании двух фаз (В и С) без земли в качестве опорного следует принимать ток jI_2кA . Тогда формулы (18) и (19) не изменятся, но анализ следует вести в плоскости сопротивления петли междуфазного КЗ. Например, при КЗ между фазами В и С:

R = Re [U_ВС / (I_В – I_С )], X = Im [U_ВС / (I_В – I_С )

α = arg[ I_2A / (I_В – I_С )]+ 90˚ , β = arg[ I_2A / I_2кA ] . (20)

При КЗ двух фаз на землю опорный ток выделить не удается, но из положения выходят тем, что ведут расчет по петле междуфазного КЗ, чем исключается влияние общего переходного сопротивления (на землю), но не исключается влияние фазных переходных сопротивлений. При КЗ трех фаз исключить влияние переходных сопротивлений при одностороннем замере вообще не удается.

ВАРИАНТЫ СПОСОБОВ ОДНОСТОРОННЕГО ЗАМЕРА

Техническая реализация одностороннего замера возможна многими путями, но все дают один и тот же результат. Перечислим некоторые известные варианты применительно к однофазным замыканиям.

ИТЕРАЦИОННЫЙ РАСЧЕТ. Сущность его заключается в постепенном приближении к искомой точке КЗ от некоторой начальной точки, взятой произвольно. Критериев, определяющих направление передвижения и конец поиска, может быть несколько. В [6] в качестве критерия предложено направление вектора

3I₀

ΔZ_УД = —————— , (21)

С_{0 Р} (I_Ф+КI₀)

где С_{0 Р} = (Z₀₀ – Z_{0 С} – Z_{0 К} ) / Z₀₀ = I₀ /I_0К (22)

-коэффициент токораспределения по схеме нулевой последовательности,

Z_{0 С} Z_{0 К,} Z₀₀ - сопротивления прилегающей системы, линии до точки КЗ и суммарное сопротивление всей схемы нулевой последовательности.

Можно сказать, что ΔZ_УД - "кажущееся" с данного конца линии сопротивление одного Ома переходного сопротивления. В [6] показано, что если в ходе расчета принять слишком малое предполагаемое расстояние до предполагаемого места КЗ, то угол arg(ΔZ/ ΔZ_УД ) положителен. Если расстояние преувеличено, угол отрицателен. При точном значении расстояния угол равен нулю. Особенно целесообразно применять итерационные расчеты на длинных линиях, где с удалением точки КЗ меняется и значение, и фаза тока нулевой последовательности.

РАСЧЕТЫ ЗНАЧЕНИЙ ЦЕЛЕВЫХ ФУНКЦИЙ ПРИ ПЕРЕМЕЩЕНИИ ПРЕДПОЛАГАЕМОГО МЕСТА КЗ ВДОЛЬ ЛИНИИ. В разделе 2 уже описан способ идентификации параметров линии, основанный на расчете значений целевых функций при перемещении предполагаемого места КЗ вдоль всей длины линии. В качестве прямой целевой функции можно использовать значение реактивной мощности в точке КЗ - по выражению (4). Однако для этого следует знать I_ƒ - ток в переходном сопротивлении, что возможно только при двустороннем замере. В [7] введено понятие косвенной целевой функции, когда ток в переходном сопротивлении заменяют близким ему по фазе током. Как показано в предыдущем параграфе, в качестве опорного можно взять токи нулевой или обратной последовательностей, можно взять аварийную составляющую тока прямой последовательности либо тока фазы. Тогда выражение (4) приобретает вид:

*

Q₀ = Im [U_ƒ I₀ ] = 0 ;

*

Q₂ = Im [U_ƒ I₂ ] = 0 ; (23)

*

Q_ав = Im [U_ƒ I_ав ] = 0 .

Можно строить графики изменения целевой функции при перемещении предполагаемого места КЗ вдоль линии (как на рис.3). Тогда точка КЗ определяется по пересечению графика с осью линии. Можно сразу сосчитать значение целевой функции в месте установки прибора и поделить его на потери реактивной мощности в одном километре линии. Все равно результат будет один и тот же и точно совпадет с результатом расчета по формуле (19).

ОПРЕДЕЛЕНИЕ МЕСТА КЗ ПО МГНОВЕННЫМ ЗНАЧЕНИЯМ ТОКОВ И НАПРЯЖЕНИЙ. Способы ООМКЗ, рассмотренные выше, основаны на расчетах по интегральным параметрам электрических величин (токов, напряжений). Термин интегральные параметры появился с внедрением ЭВМ в технику релейной защиты для того, чтобы отличить мгновенные значения синусоидальных электрических величин i, u от характеризующих эти величины в любой момент времени параметров I, U. Употребляется термин в том смысле, что ЭВМ получает интегральные параметры путем замера и обработки ряда мгновенных значений, т.е. после суммирования - интегрирования информации о мгновенных значениях.

Однако известны и способы ООМКЗ на основе операций с мгновенными значениями токов и напряжений. Первый из них предложен во Франции [8]. Основы его следующие.

Пусть однофазное КЗ через сопротивление R_П произошло на расстоянии l на линии с удельными параметрами R_УД, L_УД . Мгновенное значение напряжения на данном конце линии равно: u = l (R_УД i + L_УД 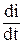) + R_П i_К ; удельное падение напряжения на одном километре линии равно: Δu = R_УД i + L_УД 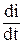= (i_Ф+ K i₀ ).* Z_{1УД .}

Если выбрать момент, когда ток в месте КЗ i_К равен нулю, то в формуле для напряжения исчезнет слагаемое, содержащее R_П . Тогда получаем простую формулу:

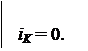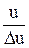l = (24)

Т.е. для определения расстояния достаточно измерить напряжение u и ток i = (i_Ф+ K i₀ ) в момент перехода тока i_К через нулевое мгновенное значение. Поскольку ток i_К неизвестен, достаточно взять почти совпадающий с ним по фазе ток i₀ . В [6] показано, что результат в точности совпадает с расчетом по интегральным значениям с применением формулы (19).

С учетом (24) просто понять формулу, по которой определяется расстояние до места однофазного КЗ в приборах МИР, ФПМ, ИМФ:

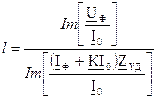. (25)

В формуле замер мгновенных значений u и Δu в момент перехода i₀ через нулевое мгновенное значение заменен на расчет проекции на мнимую ось, перпендикулярную вектору I₀ , интегральных величин U_Ф и Δ U_Ф.

Все перечисленные способы применимы и при двухфазных КЗ без земли при замене параметров петли фаза - земля на параметры петли фаза - фаза.

УЧЕТ ВЗАИМНЫХ ИНДУКЦИЙ С ДРУГИМИ ЛИНИЯМИ. Выпускаемые в настоящее время приборы способны учесть взаимную индукцию с одной из параллельных линий, для чего к прибору подводится ток нулевой последовательности этой линии I_{0 II} . При наличии взаимоиндукции по всей длине линии в формуле (25) для расстояния до места однофазного КЗ вместо (I_Ф +KI₀ ) появляется (I_Ф +KI₀+K_m I_{0 II}), где K_m = Х_m /Х₁ - коэффициент компенсации по току нулевой последовательности параллельной линии. При других видах замыканий - трехфазных, двухфазных или двухфазных на землю взаимоиндукция не учитывается, поскольку весь расчет идет по петле междуфазного КЗ.

Если взаимоиндукция имеется не по всей длине линии, а лишь на начальном участке, то вначале расчет ведут с учетом взаимоиндукции. Но если результат расчета окажется большим, чем длина участка с взаимоиндукцией l_m , то производят пересчет с "мысленным переносом" прибора в точку конца участка с взаимоиндукцией. Напряжение фазы в указанной точке равно

U_{Ф m} =U_Ф - (I_Ф +KI₀+K_m I_{0 II}) l_m Z_{1 УД} ,

токи всех фаз за пределами участка с взаимоиндукцией те же, что и в месте замера. Поэтому пересчет расстояния после "мысленного переноса" прибора не представляет трудностей.

Имеются программы, учитывающие до десяти взаимоиндукций с разной протяженностью. Идея та же - расчет начинается с головного участка, который имеет максимальное число взаимоиндукций; затем прибор "мысленно переносится" на начало все новых участков, каждый из которых имеет меньшее число взаимоиндукций, пока расстояние не окажется лежащим в пределах очередного рассмотренного участка.

УЧЕТ ОТВЕТВЛЕНИЙ С ТРАНСФОРМАТОРАМИ С ЗАЗЕМЛЕННЫМИ НЕЙТРАЛЯМИ. Схема линии с одним ответвлением приведена на рис.6. Если нейтраль трансформатора не заземлена, то влиянием ответвления можно пренебречь, поскольку токи нагрузки много больше токов короткого замыкания. При заземленной нейтрали расчет расстояния за ответвлением без учета подпитки от нейтрали будет неточен, поскольку указанная подпитка соизмерима с токами нулевой последовательности в месте замера. В этом случае расчет также ведется с "мысленным переносом прибора". Вначале расстояние считается по электрическим величинам в точке замера без учета ответвления. Если подсчитанное расстояние меньше L_ОТ, то расчет заканчивается. Но если больше, то расчет повторяется с "переносом прибора" в точку ответвления. Напряжение нулевой последовательности в указанной точке равно U_0Б = U₀ – I₀ L_ОТ Z_{0 УД} : ток нулевой последовательности за точкой ответвления равен I_0Б = I₀ - U_0Б / jХ_ОТ . Напряжения и токи других последовательностей при переходе за точку ответвления не изменяются. Поэтому последовательность расчета после "переноса прибора" в точку Б остается той же, что и для линии без ответвлений.

ПОГРЕШНОСТИ ОДНОСТОРОННЕГО ОПРЕДЕЛЕНИЯ МЕСТА ЗАМЫКАНИЯ

Рассмотренные способы имеют ряд источников погрешностей. Некоторые из них общие с любыми устройствами, работающими на дистанционном принципе - неточность работы трансформаторов тока и трансформаторов напряжения, влияние свободных составляющих переходного электромагнитного процесса, неточность знания параметров обслуживаемой линии. Но есть и специфические источники методической погрешности - влияние взаимных индукций с другими линиями и влияние комплексности токораспределения по схеме нулевой последовательности.

Влияние взаимоиндукций сказывается, если этих взаимоиндукций больше, чем может учесть прибор. Приборы МИР, ФПМ, ИМФ способны учесть влияние лишь одной взаимной индукции (у них есть входы для токов трех фаз обслуживаемой линии и для тока нулевой последовательности еще одной линии). Между тем из соображений экономии земли линии от подстанции обычно отходят коридорами, создавая многочисленные взаимоиндукции. Из всех взаимоиндукций приходится выбирать одну - наиболее сильно влияющую. Неучет остальных вызывает погрешности замера.

Принципиально указанную погрешность можно устранить создавая систему сбора информации от всех линий, отходящих по данному коридору. Подобные системы известны и существуют компьютерные программы, ведущие расчеты по данным многих приборов. Еще проще решается проблема, если на подстанции установлены цифровые осциллографы, собирающие информацию со всех присоединений. Компьютер, в который сходится информация, способен учесть взаимное влияние всех линий.

Проблема становится практически неразрешимой, если взаимные индукции появляются где-то в середине линии (взаимное сближение линий, отходящих от разных подстанций), или если коридор с взаимными индукциями появляется на противоположной по отношению к прибору стороне линии. Тогда приходится применять другие способы (например, устанавливать приборы на двух концах линии и вести расчеты по двустороннему замеру величин обратной последовательности).

Комплексность токораспределения по схеме нулевой последовательности - комплексность коэффициента токораспределения C_0p , определяемого выражением (22). Если коэффициент является комплексным числом, то ток нулевой последовательности в месте замера имеет угол с током в переходном сопротивлении. В общем случае этот угол всегда имеется, поскольку в схеме рис.2 сопротивление нулевой последовательности систем почти чисто индуктивно, а сопротивление линии имеет значительную активную составляющую (из-за потерь активной мощности в земле).

С формальной точки зрения погрешность появляется потому, что не имея точной информации о фазе тока в переходном сопротивлении, приборы вынуждены вести расчет не по точной формуле (18), а по приближенной формуле (19), не учитывающей угла β = arg(C_0p).

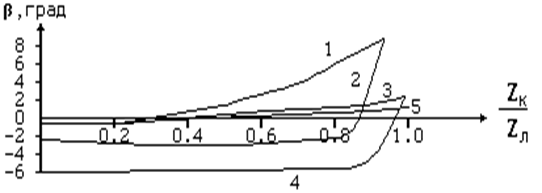Сам угол β невелик. О значении этого угла можно судить по рис.18, на котором показана его зависимость от расстояния при перемещении точки КЗ по одиночной линии с сопротивлением Z_0Л = 35 e^j78˚ Ом.

Рис.18.Изменение угла и при удалении точки КЗ:

1-Z_0с1 =j1 Ом, Z_0с2 =j 10 Ом; 2- Z_0с1 =j10 Ом, Z_0с2 =j 1 Ом;

3- Z_0с1 =j10 Ом, Z_0с2 =j 100 Ом; 4- Z_0с1 =j100 Ом, Z_0с2 =j 10 Ом;

5- Z_0с1 =j1 Ом, Z_0с2 =j 10 Ом

Принят довольно широкий диапазон изменения сопротивления систем (с1-прилегающая к месту установки устройства система, с2- система противоположного конца линии). При индуктивных системах и активно-индуктивной линии угол β при КЗ в начале линии всегда отрицателен, при КЗ в конце линии всегда положителен.

На линии всегда имеется точка с β=0, при КЗ в которой погрешность замера равна нулю при любом переходном сопротивлении. Погрешность при КЗ в других точках зависит от величины переходного сопротивления, от значения угла β и от токов нагрузочного режима. Примеры зависимости погрешности от расстояния и от составляющих нагрузочного режима приведены на рис.19. Рассматривалось КЗ через переходное сопротивление в 30 Ом на линии 220 кВ с параметрами, приведенными в разделе 2 (см. также рис.3 и рис.16).

Токи нагрузочного режима определены углом между ЭДС систем (δ=arg(E₂ / E₁ ). Отрицательные углы между ЭДС - передающий конец линии. Положительные углы - приемный конец линии. Видно, что при КЗ в начале линии погрешности невелики, при КЗ в конце могут быть весьма большие (положительные погрешности соответствуют заниженному результату расчета). На передающем конце линии погрешности всегда малы, на приемном могут быть весьма значительными.

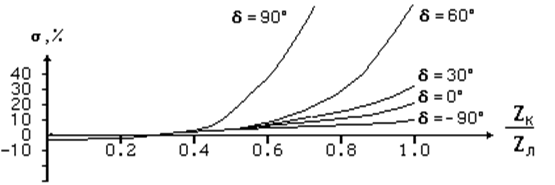Рис.19. Погрешности замера от комплексности токораспределения

Причина больших погрешностей ясна из рассмотрения годографов рис.16. На передающем конце линии годограф всегда лежит в первом квадранте, вектор ΔZ невелик и погрешности от неучета угла величиной в несколько градусов незначительны. На приемном конце линии годограф переходит из первого во второй квадрант комплексной плоскости сопротивлений. Когда сопротивление на зажимах близко к оси сопротивления линии, даже незначительная ошибка по углу приводит к большой погрешности расчета.

Известны пути уменьшения влияния комплексности токораспределения. Согласно [6] для этого следует решать совместно уравнения (18) зависимость расстояния от электрических величин и (22) - зависимость β от расстояния. В результате получается квадратное уравнение, один из корней которого дает искомое расстояние.

Другой путь - предложенное в [7] использование прямой целевой функции. Однако уже указано, что это возможно только при двустороннем замере.