Передаточная функция как форма записи диф. уравнения в теории автоматического управления

Передаточной функцией системы или элемента называют отношение выходной величины к входной при нулевых начальных условиях.

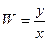
Передаточная функция может быть записана в 4 формах:

1. операторная.

Введем в уравнение оператор дифференцирования «р» 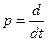, тогда

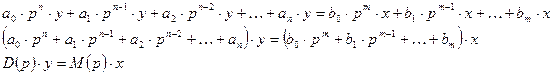
D(p) – характеристический многочлен, а 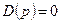- характеристическое уравнение.

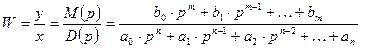
2. стандартная.

Преобразуем к виду:

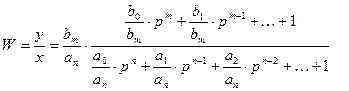
это стандартная форма записи передаточной функции.

Величина 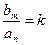называется коэффициентом передачи системы,

Величины 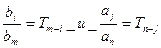- постоянные времени. Тогда примет вид:

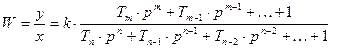
3. в форме изображений по Лапласу.

Для получения передаточной функции в форме изображений по Лапласу используют преобразования, приводящие функцию действительного аргумента t в функцию мнимого переменного р.

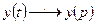- преобразование Лапласа

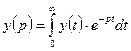
Рассмотрим уравнение/ Преобразуем функцию y(t) по Лапласу.

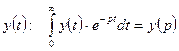
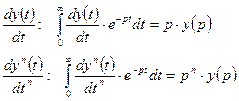
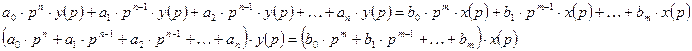
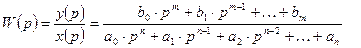
обратное преобразование Лапласа преобразует функцию комплексного переменного р в функцию действительного переменного t.

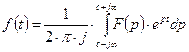
Свойства:

1).

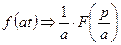
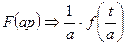
2). Если 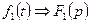, , 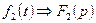то:

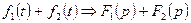
3).

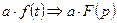
4). если оригинал смещается на некоторую величину 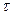, причем 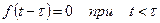и 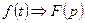, то смещенная функция примет вид:

.

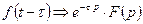5). Если изображение смещается на р₀, то оно соответственно будет равно:.

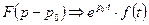
6). Произведение 2 изображений равно:

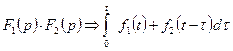
7).

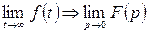
8). Свойство дифференцирования. Если 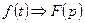и f(t) непрерывно дифференцируема, то производная порядка n будет равна:

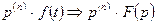
9). Свойство интегрирования.

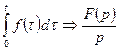
4. частотная.

Частотную форму передаточной функции можно записать в показательной форме, и тогда она примет вид:

Частотная передаточная функция, 3 формы ее записи.

В передаточной функции в форме преобразований по Лапласу р является комплексной переменной. Ее вид 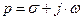. Пусть 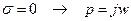(комплексная переменная является чисто мнимой), тогда получим передаточную функцию в частотной форме:

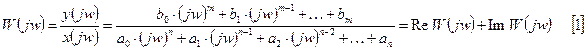
Частотную форму передаточной функции можно записать в показательной форме, и тогда она примет вид:

Соединение звеньев

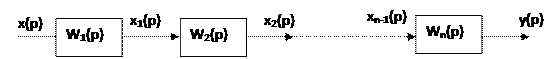При последовательном соединении выходная величина каждого предшествующего звена является входным воздействием последующего звена.

При преобразовании структурных схем цепочку из последовательно соединенных звеньев можно заменить одним звеном с передаточной функцией W_экв(p), которую находят следующим образом:

Записывают уравнения последовательно соединенных звеньев:

x₁(p)= x(p)∙W₁(p); x₂(p)= x₁(p)∙W₂(p), …;

y(p)=x_n-1(p)∙W_n(p).

Исключив из этой системы x₁, x₂, … ,x_n-1, получим:

y(p)= W₁(p)∙W₂(p)∙ … ∙W_n(p)∙x(p);

откуда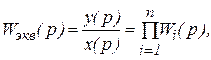

т.е. передаточная функция последовательного соединения звеньев определяется как произведение передаточных функций звеньев, включенных последовательно.

При параллельном соединении на вход всех звеньев подается один и тот же сигнал, а выходящие величины алгебраически складываются:

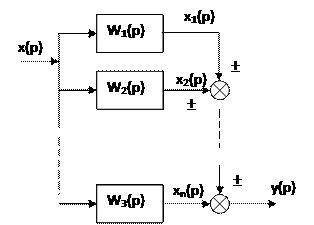
Эту цепь нужно заменить одним звеном с передаточной функцией W_экв(p):

Составим уравнения для каждого из звеньев цепочки:

x₁p)= x(p)∙W₁(p); x₂(p)=x(p)∙W₂(p); … ;

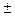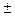x_n(p)=x(p)∙W_n(p); y(p)= x₁(p) x₂(p) … x_n(p)

Исключив из этой системы x₁, x₂,…,x_n, получим:

y(p)= 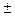x(p)[W₁(p)+W₂(p)+…+W_n(p)],

откуда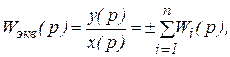

т.е. передаточная функция параллельного соединения звеньев определяется как алгебраическая сумма передаточных функций звеньев, включенных параллельно.