Решение систем по формулам Крамера.

Задача № 1. Решить по формулам Крамера систему .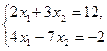

Решение. Матричный метод. Обозначим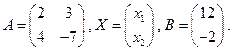

Тогда система запишется в виде AX=B . Ее решение равно 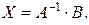Определитель матрицы А равен 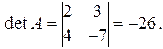Алгебраические дополнения элементов матрицы А равны 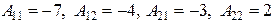. Далее,

. .

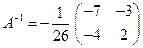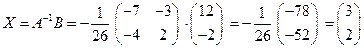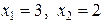
По формулам Крамера имеем

.

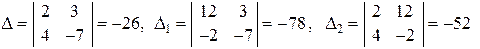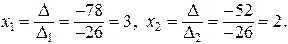
Ответ. .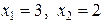

Задача № 2. (Типовая) Решить систему линейных уравнений по формулам Крамера

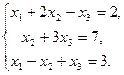
Решение. Вычислим главный определитель системы .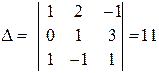

Вспомогательные определители равны

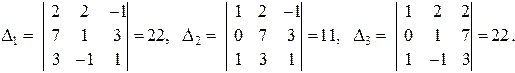
Тогда по формулам Крамера

.

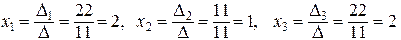Задача № 3. (Типовая) Решить в случае совместности систему линейных уравнений по формулам Крамера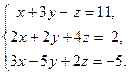

Решение.Вычислим главный определитель системы

.

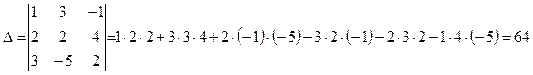Вспомогательные определители равны

, , .

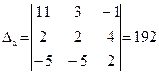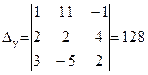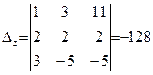Тогда по формулам Крамера

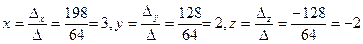
Задача №4. Решить в случае совместности систему линейных уравнений

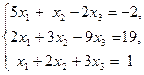
Решение.Составляем матрицу систему 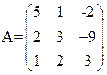.Определитель этой матрицы равен

.

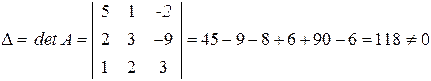Вспомогательные определители равны

.

.

.

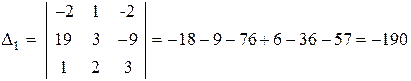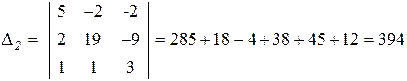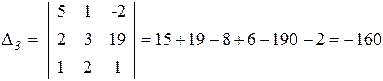Тогда по формулам Крамера

.

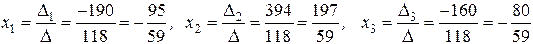Ответ. .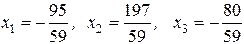

Решение систем матричным методом.

Задача № 1. (Типовая) Решить систему линейных уравнений матричным методом

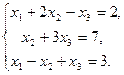
Решение. Решим исходную систему матричным методом. Составим матрицы

.

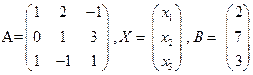Определитель матрицы А равен 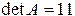. Вычислим алгебраические дополнения.

,

,

.

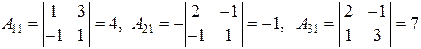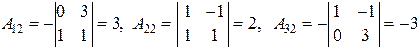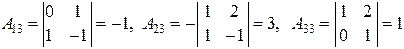Обратная матрица

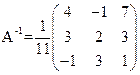
Решение системы .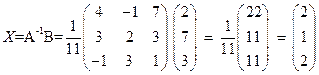

Ответ. .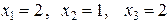

Исследование систем на совместность.

Задача № 1. (Типовая) Исследовать на совместность систему

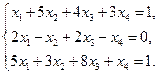
Решение.

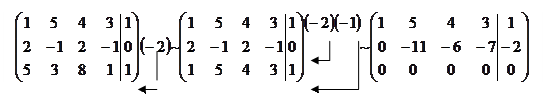Получена ступенчатая матрица. Из нее следует 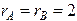, ранг иатрцы системы равен рангу расширенной матрицы. Система совместна.

Задача №2. Исследовать на совместность систему уравнений:

;

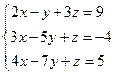Решение. Здесь имеем случай, когда определитель матрицы системы

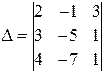равен нулю.

Поэтому буквально правило Крамера применить нельзя. Однако если мы подсчитаем определитель :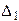

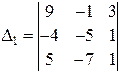, то обнаружим, что он отличен от нуля 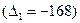, отсюда заключаем, что система несовместна. В самом деле, при выводе правила Крамера мы переходим от данных уравнений к уравнениям

.

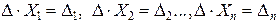Отсюда: если 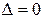, а из определителей 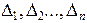хотя бы один не равен нулю, то исходная система уравнений несовместна.

Решение систем методом Гаусса.

Задача № 1. (Типовая) Решить систему линейных уравнений: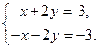

Решение1. Исследование на совместность.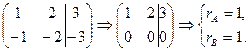

Следовательно, 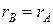и система совместна.

2. Ищем число свободных параметров

n - r=2-1=1 - один свободный параметр.

3. Ищем неизвестные.

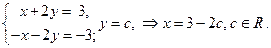
Ответ: .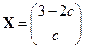

Задача № 2. (Типовая) Решить в случае совместности систему линейных уравнений

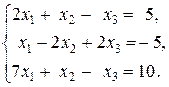
Решение. Составляем расширенную матрицу.

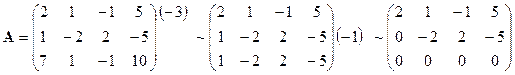
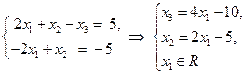Ранг расширенной матрицы системы равен рангу матрицы системы и меньше числа неизвестных, следовательно, система имеет бесконечное множество решений. Найдем общее решение системы. Число свободных переменных равно 3-2=1.

Задача № 3. (Типовая) Решить в случае совместности систему линейных уравнений

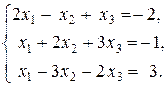
Решение. Составляем расширенную матрицу.

.

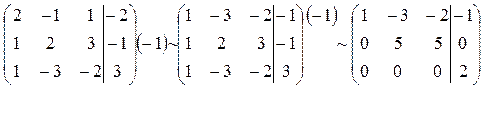, следовательно, система несовместна.

Ответ: система несовместна.