Интегральные критерии качества
Интегральные критерии позволяют судить о качестве управления путем вычисления интегралов от некоторых функций управляемой величины. Эта функция выбирается таким путем, чтобы значение определенного интеграла от этой функции по времени от 0 до + 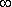 было однозначно связано с качеством переходного процесса. В то же время данный интеграл должен сравнительно просто вычисляться через коэффициенты уравнений исследуемой системы.
было однозначно связано с качеством переходного процесса. В то же время данный интеграл должен сравнительно просто вычисляться через коэффициенты уравнений исследуемой системы.
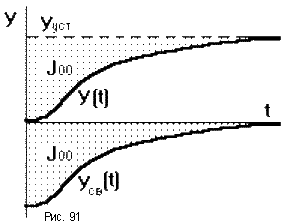 Например, если переходная характеристика является монотонной, то можно утверждать, что качество переходного процесса тем лучше, чем меньше площадь, ограниченная данной кривой и установившимся значением управляемой величины (рис.91). Она равна площади, ограниченной кривой изменения свободной составляющей управляемой величины и осью абсцисс.
Например, если переходная характеристика является монотонной, то можно утверждать, что качество переходного процесса тем лучше, чем меньше площадь, ограниченная данной кривой и установившимся значением управляемой величины (рис.91). Она равна площади, ограниченной кривой изменения свободной составляющей управляемой величины и осью абсцисс.
Если система устойчива, то свободная составляющая управляемой величины в пределе стремится к нулю 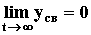 , поэтому площадь ограниченная данной кривой имеет конечное значение и определяется по формуле:
, поэтому площадь ограниченная данной кривой имеет конечное значение и определяется по формуле:
Joo = 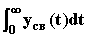 .
.
Величина Joo представляет собой линейную оценку качества управления. 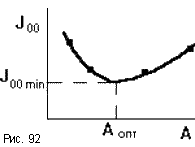 Чем она меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум Joo. Если имеется какой то варьируемы параметр A, то можно построить кривуюJoo = f(A) (рис.92). Ее минимум, определяемый из условияdJoo/dA = 0, даст оптимальное значение A.
Чем она меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум Joo. Если имеется какой то варьируемы параметр A, то можно построить кривуюJoo = f(A) (рис.92). Ее минимум, определяемый из условияdJoo/dA = 0, даст оптимальное значение A.
Пусть дано уравнение динамики замкнутой САУ:
(a0pn + a1pn-1 + a2pn-2 + ... + an)y = (b0pm + b1pm-1 + ... + bm)u.
Свободный процесс описывается однородным дифференциальным уравнением:
(a0pn + a1pn-1 + ... + an)yсв = 0,
следовательно:
yсв = 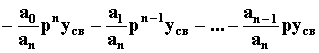
yсв = 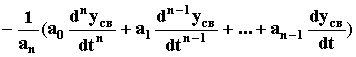
Joo = 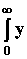 св(t)dt =
св(t)dt = 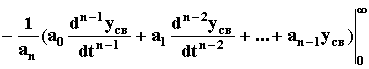 .
.
Пусть при t = 0 САУ имела следующие начальные условия:
yсв(0) = y0, 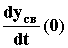 = y0’, ...,
= y0’, ..., 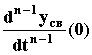 = y0(n-1).
= y0(n-1).
Кроме того
yсв( 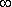 ) = 0,
) = 0, 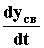 (
( 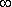 ) = 0,...,
) = 0,..., 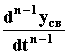 (
( 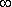 ) = 0,
) = 0,
так как процесс затухает и при t 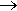
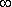 свободная составляющая и все производные становятся равны нулю. Подставляя эти значение, получаем:
свободная составляющая и все производные становятся равны нулю. Подставляя эти значение, получаем:
Joo = (a0y0(n-1) + a1y0(n-1) + ... + an-1y0)/(an.
То есть линейную оценку качества регулирования можно легко вычислить, зная начальные условия и коэффициенты дифференциального уравнения. Возможны и другие линейные оценки качества, но они используются реже, например:
J01 = 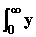 св(t)
св(t) 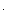 t
t 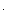 dt;
dt;
J0n = 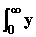 св(t)
св(t) 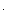 tndt.
tndt.
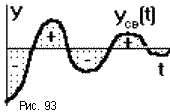 Линейные оценки качества неприменимы при колебательном процессе. Так как площади, ограниченные кривой yсв(t) и осью абсцисс складываются с учетом знака, то минимальному значению Joo может соответствовать процесс с большим числом колебаний и малым быстродействием (рис.93). В этом случае более эффективны квадратичные оценки качества, например,
Линейные оценки качества неприменимы при колебательном процессе. Так как площади, ограниченные кривой yсв(t) и осью абсцисс складываются с учетом знака, то минимальному значению Joo может соответствовать процесс с большим числом колебаний и малым быстродействием (рис.93). В этом случае более эффективны квадратичные оценки качества, например,
J20 = 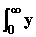 yсв2(t)dt.
yсв2(t)dt.
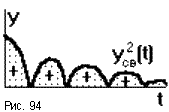 Значение этого интеграла соответствует площади под кривой yсв2(t)и осью абсцисс, которая всегда положительна (рис.94).
Значение этого интеграла соответствует площади под кривой yсв2(t)и осью абсцисс, которая всегда положительна (рис.94).
Выбирая параметры САУ по минимуму J20 мы приближаем кривую yсв(t) к осям координат, что приводит к уменьшению времени регулирования (рис.95). Вывод формулы для вычисления этой оценки сложен, поэтому ограничимся замечанием, что значение вычисляется через коэффициенты дифференциального уравнения a0...an,b0...bm. При вычислении слагаемых в этой формуле используются определители Гурвица, так что даже расчет по ней сопряжен с определенными трудностями и требует использования ЭВМ или специальных таблиц.
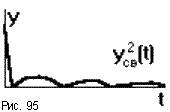 При выборе параметров САУ по минимуму J20 часто получают нежелательную колебательность процесса, так как приближение yсв(t) к оси ординат вызывает резкое увеличение начальной скорости, что в свою очередь может вызвать большое перерегулирование, уменьшив при этом запас устойчивости. Для того, чтобы обеспечить плавность протекания процесса, в квадратичную оценку качества добавляется слагаемое, зависящее от скорости изменения регулируемого параметра yсв’(t). Получаем критерий качества
При выборе параметров САУ по минимуму J20 часто получают нежелательную колебательность процесса, так как приближение yсв(t) к оси ординат вызывает резкое увеличение начальной скорости, что в свою очередь может вызвать большое перерегулирование, уменьшив при этом запас устойчивости. Для того, чтобы обеспечить плавность протекания процесса, в квадратичную оценку качества добавляется слагаемое, зависящее от скорости изменения регулируемого параметра yсв’(t). Получаем критерий качества
J21 = 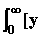 св2(t) + t2
св2(t) + t2 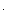 (yсв’(t))2]dt,
(yсв’(t))2]dt,
где  - некоторая наперед заданная постоянная времени, определяющая весовое соотношение между оценкой по yсв и по yсв’. При малых значениях
- некоторая наперед заданная постоянная времени, определяющая весовое соотношение между оценкой по yсв и по yсв’. При малых значениях уменьшение колебательности будет незначительным. Завышение
уменьшение колебательности будет незначительным. Завышение  увеличит время переходного процесса так, что ее выбор определяется конкретными условиями.
увеличит время переходного процесса так, что ее выбор определяется конкретными условиями.
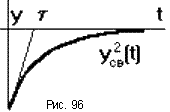 Этот интеграл имеет наименьшее значение, если переходный процесс соответствует экспоненте с постоянной времени
Этот интеграл имеет наименьшее значение, если переходный процесс соответствует экспоненте с постоянной времени  (рис.96). Другими словами, по соображениям качества управления следует стремиться к тому, чтобы переходная характеристика замкнутой САУ как можно меньше отличалась от характеристики инерционного звена первого порядка, имеющего наперед заданную постоянную времени
(рис.96). Другими словами, по соображениям качества управления следует стремиться к тому, чтобы переходная характеристика замкнутой САУ как можно меньше отличалась от характеристики инерционного звена первого порядка, имеющего наперед заданную постоянную времени  , значение которой определяются техническими условиями.
, значение которой определяются техническими условиями.
Задача выбора параметров САУ по минимумуJ20 и J21 решается аналитически только в случае невысокого порядка дифференциального уравнения. Иначе используют ЭВМ.
Вопросы
- Как влияет на качество управления близость корня характеристического полинома САУ к мнимой оси комплексной плоскости?
- Как влияет на качество управления угол раскрытия трапеции области корней?
- Как определить степень устойчивости САУ?
- Как определить колебательность САУ?
- Как можно вычислить время переходного процесса, зная как расположены корни характеристического полинома на комплексной плоскости?
- Как построить мажоранту и миноранту, ограничивающую кривую переходного процесса САУ?
- Что называется интегральными критериями качества САУ?
- Как определить линейную и квадратичную оценки качества управления?
- В чем недостатки линейной и квадратичной оценок качества управления?
- Как выглядит оценка качества управления, способствующая приближению кривой переходного процесса к экспоненте?
Теоретическое обоснование
Частотные методы основаны на привычном для инженеров графическом изображении динамических характеристик, которые можно снять экспериментально, поэтому они находят широкое применение. В частности зная АФЧХ разомкнутой САУ Wp(j  ), можно построить АФЧХ замкнутой САУ
), можно построить АФЧХ замкнутой САУ
Wз(j  ) =
) = 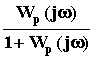 = Pз(
= Pз(  ) + jQз(
) + jQз(  ),
),
а по ней - требуемую для частотных методов вещественную ЧХ замкнутой САУ Pз(  ). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристику САУ h(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.
). Зная ВЧХ замкнутой САУ, можно приближенно построить переходную характеристику САУ h(t), которую снять экспериментально очень трудно, и по ней определить показатели качества управления.
Теоретическое обоснование этого в том, что любую функцию, в том числе и единичную ступенчатую, можно разложить в ряд Фурье:
1(t) = A0 + 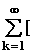 Ak1cos(k
Ak1cos(k  t) + Ak2sin(k
t) + Ak2sin(k  t)].
t)].
Так как замкнутая САУ линейна, то при подаче на вход суммы сигналов с выхода снимается сигнал, равный сумме реакций на каждый из входных сигналов. Входному сигналу ui(wi,t) на выходе будет соответствовать составляющая выходного сигналаyi(  i,t) = W(j
i,t) = W(j  i)
i) 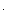 ui(
ui(  i,t), тогда
i,t), тогда
h(t) = 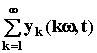 = A0W(0) +
= A0W(0) +  (jkw)
(jkw) 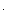 [Ak1cos(kwt) + Ak2sin(kwt)].
[Ak1cos(kwt) + Ak2sin(kwt)].
Преобразование этого выражения приводит к двум равнозначным формулам определения h(t) через составляющие ВЧХ:
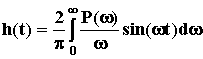 ;
; 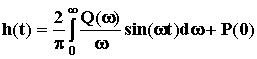 ,
,
где P(  )и Q(
)и Q(  ) - вещественная и мнимая части АФЧХ замкнутой САУ. Предпочтение обычно оказывают первой формуле, хотя с одинаковым успехом можно использовать и вторую.
) - вещественная и мнимая части АФЧХ замкнутой САУ. Предпочтение обычно оказывают первой формуле, хотя с одинаковым успехом можно использовать и вторую.
Точно вычислить эти интегралы можно только с помощью ЭВМ, но в практике нашел широкое применение приближенный способ построения переходной характеристики на основе линейной аппроксимации ВЧХ замкнутой САУ, который называется метод трапеций. Прежде, чем рассматривать этот метод, рассмотрим без доказательства основные соотношения между ВЧХ замкнутой САУ и ее переходной характеристикой.
