Статическое и астатическое регулирование

Если на управляемый процесс действует возмущение f, то важное значение имеет статическая характеристика САУ в форме y = F(f) при y_o = const. Возможны два характерных вида этих характеристик (рис.19). В соответствии с тем, какая из двух характеристик свойственна для данной САУ, различают статическое и астатическое регулирование.

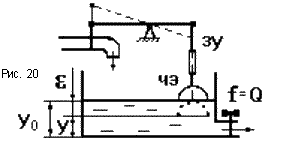
Рассмотрим систему регулирования уровня воды в баке (рис.20). Возмущающим фактора является поток Q воды из бака. Пусть при Q = 0 имеем y = y_o , e = 0. ЗУ системы настраивается так, чтобы вода при этом не поступала. При Q 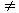0, уровень воды понижается (e 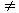0), поплавок опускается и открывает заслонку, в бак начинает поступать вода. Новое состояние равновесия достигается при равенстве входящего и выходящего потоков воды. Но в любом случае при Q 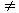0 заслонка должна быть обязательно открыта, что возможно только при e 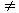0. Причем, чем больше Q, тем при больших значениях e, устанавливается новое равновесное состояние. Статическая характеристика САУ имеет характерный наклон (рис.19б). Это есть пример статического регулирования. Для получения статического регулирование, все звенья САР должны быть статическими.

Статические регуляторы работают при обязательном отклонении e регулируемой величины от требуемого значения. Это отклонение тем больше, чем больше возмущение f. Это заложено в принципе действия регулятора и не является его погрешностью, поэтому данное отклонение называется статической ошибкой регулятора. Из рис.21 видно, что, чем больше коэффициент передачи регулятора K_р, тем на большую величину откроется заслонка при одних и тех же значениях e, обеспечив в установившемся режиме большую величину потока Q. Это значит, что на статической характеристике одинаковым значениям e при больших K_р будут соответствовать большие значения возмущения Q, статическая характеристика САУ пойдет более полого. Поэтому, чтобы уменьшить статическую ошибку надо увеличивать коэффициент передачи регулятора. Того же результата можно добиться, увеличивая коэффициент передачи объекта управления, но это дело конструкторов, проектирующих данный объект, а не специалистов по автоматике.

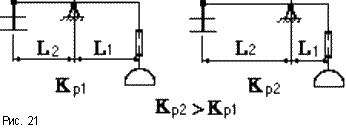
Статизм d, САР, характеризует насколько сильно значение регулируемой величины отклоняется от требуемого значения при действии возмущений, и равна тангенсу угла наклона статической характеристики, построенной в относительных единицах: d = tg(a) = 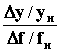(рис.22),где y = y_н,f = f_н- точка номинального режима САУ. При достаточно больших значениях K_p имеем d 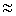1/K_p.

В некоторых случаях статическая ошибка недопустима, тогда переходят к астатическому регулированию, при котором регулируемая величина в установившемся режиме принимает точно требуемое значение независимо от величины возмущающего фактора. Статическая характеристика астатической САУ не имеет наклона (рис.19в). Возможные неточности относятся к погрешностям конкретной системы и не являются закономерными.

Для того, чтобы получить астатическое регулирование, необходимо в регулятор включить астатическое звено, например ИД, между ЧЭ и УО (рис.23).

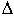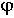
Если уровень воды понизится, то поплавок переместит движок потенциометра на величину L, за счет этого появится разность потенциалов 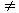0 и ИД начнет поднимать заслонку до тех пор, пока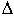 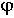не уменьшится до нуля, а это возможно только приy = y_o . При поднятии уровня воды разность потенциалов сменит знак, и двигатель будет вращаться в противоположную сторону, опуская заслонку.

Достоинства и недостатки статического и астатического регулирования: статические регуляторы обладают статической ошибкой; астатические регуляторы статической ошибки не имеют, но они более инерционны, сложны конструктивно и более дороги.

Обеспечение требуемой статической точности регулирования является первой основной задачей при расчете элементов САУ.

Вопросы

1. Перечислите и дайте краткую характеристику основных видов САУ?
2. Что называется статическим режимом САУ?
3. Что называется статическими характеристиками САУ?
4. Что называется уравнением статики САУ?
5. Что называется коэффициентом передачи, в чем отличие от коэффициента усиления?
6. В чем отличие нелинейных звеньев от линейных?
7. Как построить статическую характеристику нескольких звеньев?
8. В чем отличие астатических звеньев от статических?
9. В чем отличие астатического регулирования от статического?
10. Как сделать статическую САР астатической?
11. Что называется статической ошибкой регулятора, как ее уменьшить?
12. Что называется статизмом САР?
13. Назовите достоинства и недостатки статического и астатического регулирования?

3.1. Динамический режим САУ.
Уравнение динамики

Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины. Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.

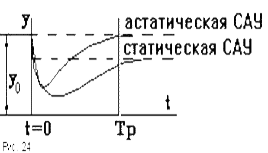
Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся значением выходной величины y = y_o. Пусть в момент t = 0 на объект воздействовал какой - либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис.24). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим.

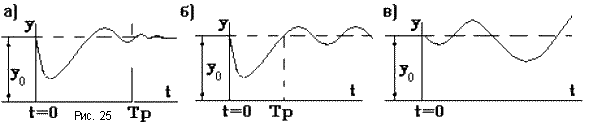
При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и такая вероятность, что после некоторого времени Т_р в системе установятся незатухающие колебания регулируемой величины - незатухающий колебательный процесс (рис.25б). Последний вид - расходящийся колебательный процесс (рис.25в).

Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся протеканием в ней переходных процессов. Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ.

Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u,f,t), описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:

F(y, y’, y”,..., y⁽ⁿ⁾, u, u’, u”,..., u^(m), f, f ’, f ”,..., f^(k)) = 0.