Потенциальная энергия деформации пластин.

Вариационные методы расчета пластин.

Точные аналитические решения получить невозможно. Поэтому применяют вариационне методы, которые позволяют решать задачи теории упругости в приблежении.

При этом не точно удовлетворяются дифференциальные уравнения и граничные условия.

В основе – вариационные принципы (например, принцип возможных перемещений, принцип Лагранжа.)

В расчете пластин вариац.методы позволяют получить приближенное решение для прогиба пластины с точностью , достаточной для практического применения.

При этом искомая функция задаётся виде уравнения, соответствующего характеру изогнутой срединной поверхности пластины и удовлетворяющая граничные условия.

Это уравнения должно содержать неизвестный коэффициент одной переменной для определения которой принимается один из варифц.принципов.

Такой подход сводит диф.уравнения к решению линейных уравнений.

Функция прогибов:

W(x,y) ∑_(k=1)^m ∑_(l=1)^n▒akl φkl (x,y), где к – 1,2,3..m . l=1,2,3..n

В этом выражении функция φkl должна быть линейно независимая удовлетворять кинематическим граничным условиям. Они задаются в начале расчета и называются аппроксимарующими.

Коэффициент аkl является постоянным числом и должен быть определен

Расчет пластин методом Ритцы-Тимошенко

Основан на теореме Дирихле-Лагранжа, в котором утверждается: потенциальная энергия упругого тела в состоянии устойчивого равновесия имеет минимальное значение.

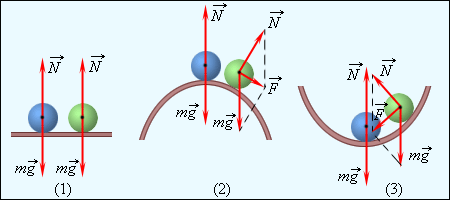1-безразличное

2 неустойчивое

3- усточйчивое

Для этого нужно составлять выражения для потенциальной энергии деформации пластины U и работы внешних сил А.

П= U-А (1)

При задании прогибов в виде (1), полная потенциальная энергия пластинки является квадратичной функцией параметров а_kl :

П=П(а_kl²)

Для выполнения условия минимума полной потенциальной энергии пластины, надо составить частные производные от П по всем параметрам а_kl

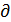П/ 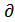а_kl =0 (2)

Уравнение (2) позволяет получить систему линейных алгебраических уравнений относительно а_kl. Найдя эти параметры и подставив в (1), получим приближенное решение задачи.

Расчет пластин методом Бубнова-Галеркина.

Расчет пластин методом Власова.

Расчет пластин методом конечных разностей.

Расчет пластин МКЭ.

1 этап. Составление КЭ схемы:

a) выбор типа КЭ ( по геометрии, виду апроксимации ……..)

б) Разбивка области на КЭ с номерами узлов и элем.

В) Описание заданных узловых нагрузок

2 этап. Формирование матриц жёсткости и вектора узловых сил.

а) Составление элементов МЖ и ВН в локальной системе координат

б) Преобразование элементов МЖ и ВН из локальной в глобальную систему координат

3 этап. Учёт заданных статических и кинематических граничных условий.