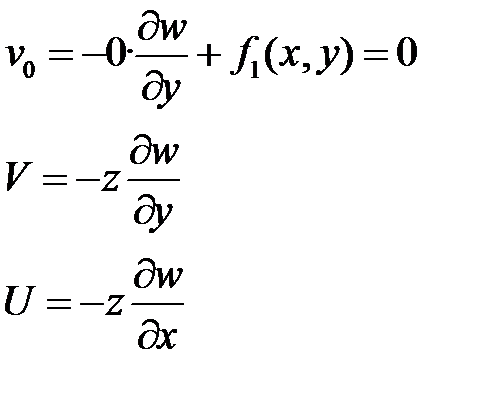Выражение перемещений и деформаций через прогибы пластины
Основные понятия, гипотезы, принимаемые при расчете пластин и следствия из них.
Пластиной называется призматическое тело, высота которого мала по сравнению с размерами в плане.
Плоскость которая делит пластину пополам называется срединной.
Линия пересечения бок. Пов. Пластинки со сред назю контуром пластины.
1) Толстые – пластины при b/h < =8….10. Расчёт производят как массивный объект.
2) Тонкие – 8….10<=b/h<=80….100
А)Жёсткие –w/h<=0.2…..0.5
Б)Гибкие- w/h > 0.2….0.5, работая на изгиб как мембрана.
3)Мембраны – b/h>=80…..100. Работаю только по закреп краям контура. Сопр на изгиб малы.
I) Гипотеза прямых номарлей.Любой линейный элемент, нормальный к срединной плоскости пластинки, остаётся прямолинейным и нормальным к срединной поверхности в процессе изгиба и длина не измен.
II) Отсутствет давление между слоями пластинки – напряжение надавливания горизонтальных слоёв пластинки друг на друга (сигма z) опускаем по сравнению с уровнями напряжений (сигма х, сигма y) . ГИПОТЕЗЫ КИРГОФА-ЛЯВА.
III) Нерастяжимости срединной поверхности – при малых прогибах (w/h <= 0,2….0,5) в срединной поверхности отсутств деформации напряжения, сжатия и сдвига нейтральна.
Выражение перемещений и деформаций через прогибы пластины
Первое допущение – длина перпендикуляра mn не измен. Т.к.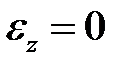 
и он не искривляется при изгибе ( 
)
------ 
---- 
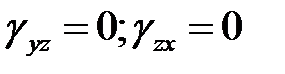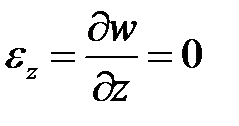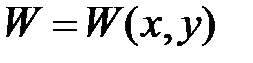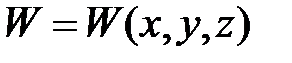
Ур-е говорит, что прогибы не зависят от Z и все точки принадлежат mn, получаем одинаковый прогиб.
Из ур-я КОШИ -----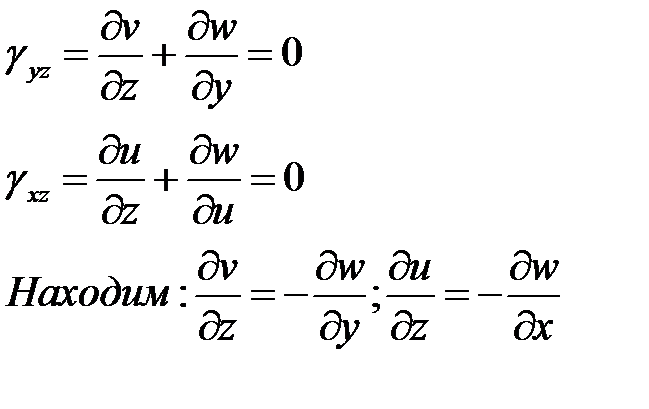 
Интегрируя по Z получаем:
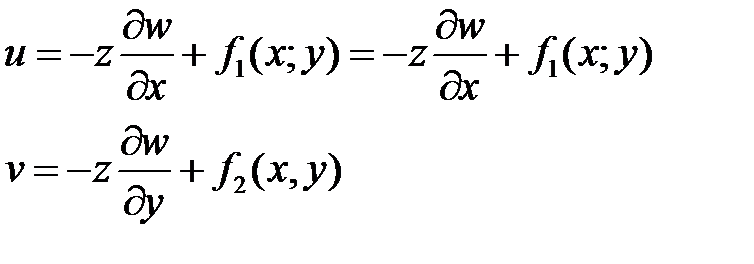
Пользуясь гипотезой нерастяжимости срединной плоскости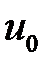 
и 
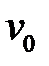при Z=0 равны 0.
Подставляя в ур-я получаем
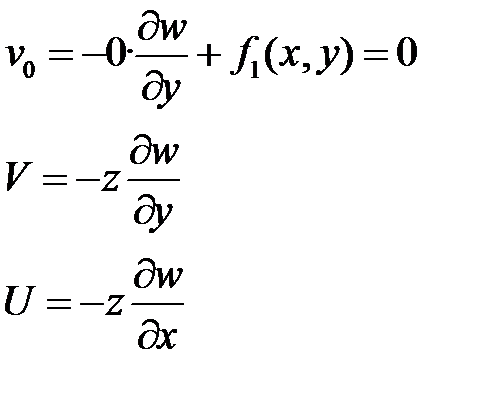
Напряжения в пластине и их выражения через прогибы
Формулы закона Гука
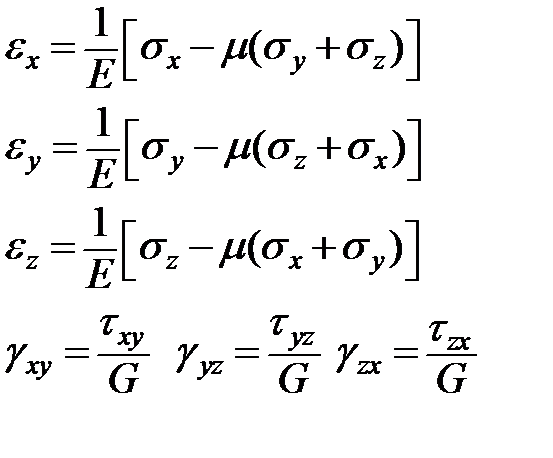
Из первой и второй гипотезы:
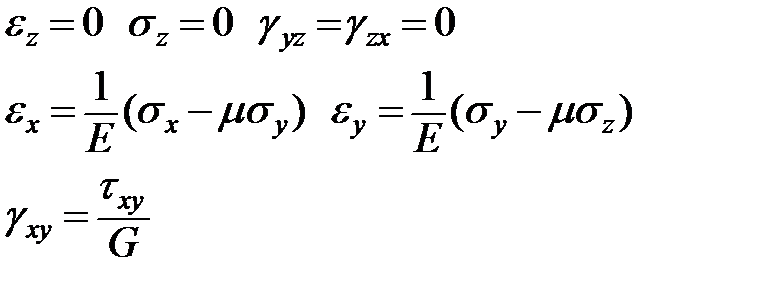
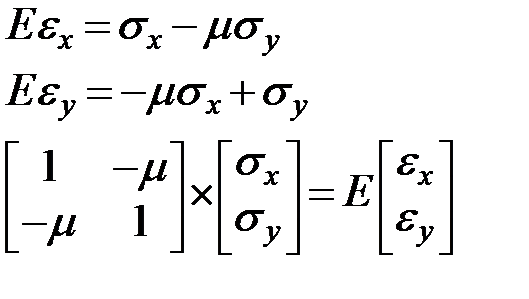
Применим правило Крамера 
-определитель из коэффициентов при неизвестных
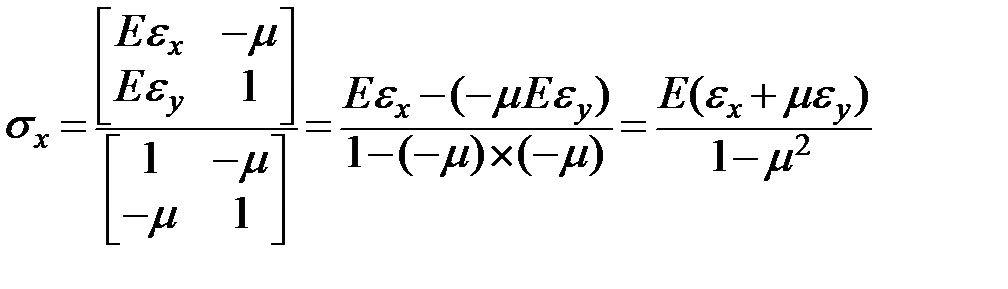
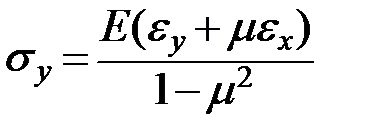
Определим напряжения заменив перемещения на дифференциальные (2,4) уравнения через прогибы
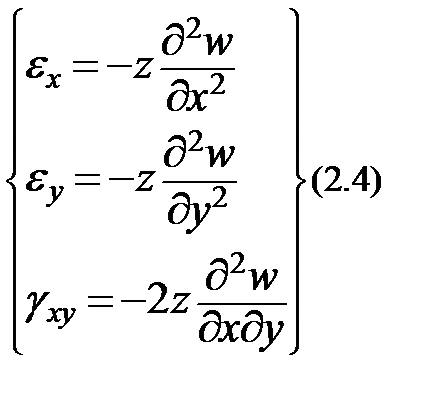
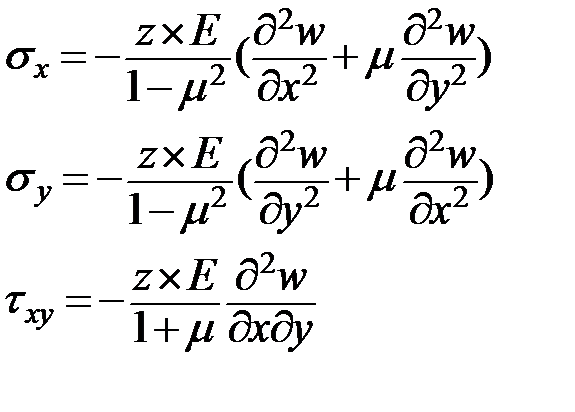
Усилия в пластинке и их выражения через прогибы
Выясним какое усилие возникнет в сечении пластинки нормальной к ее срединной поверхности:
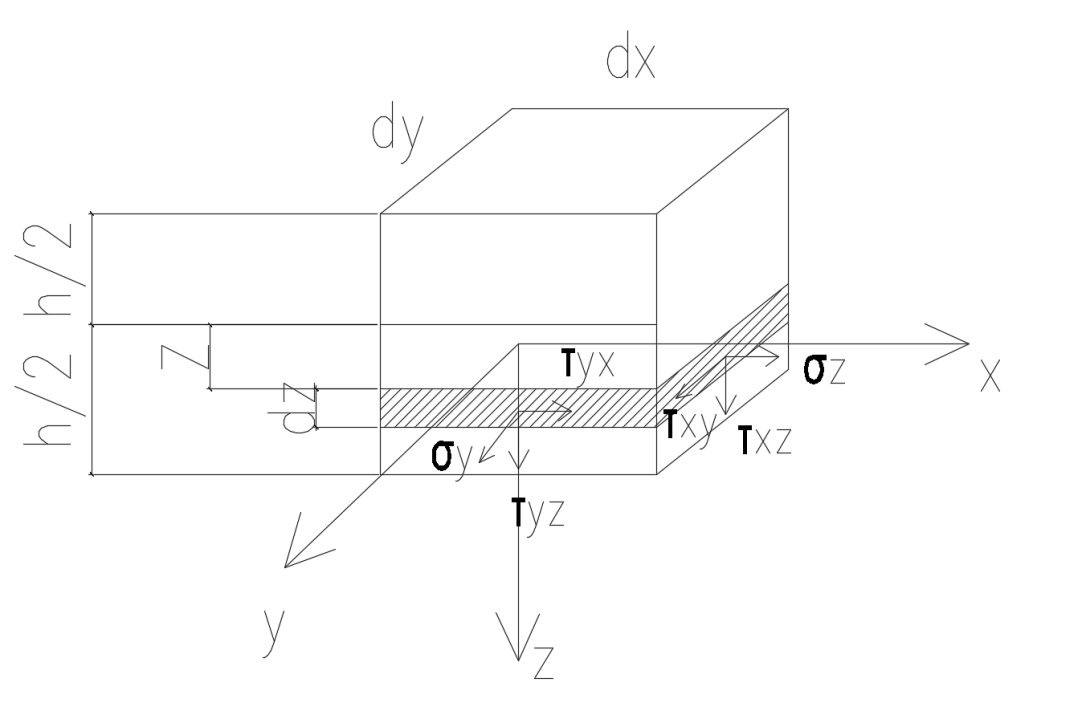
Определим приходящуюся на единице ширины сечения продольную силу N. Она равна сумме проекций на ось Х
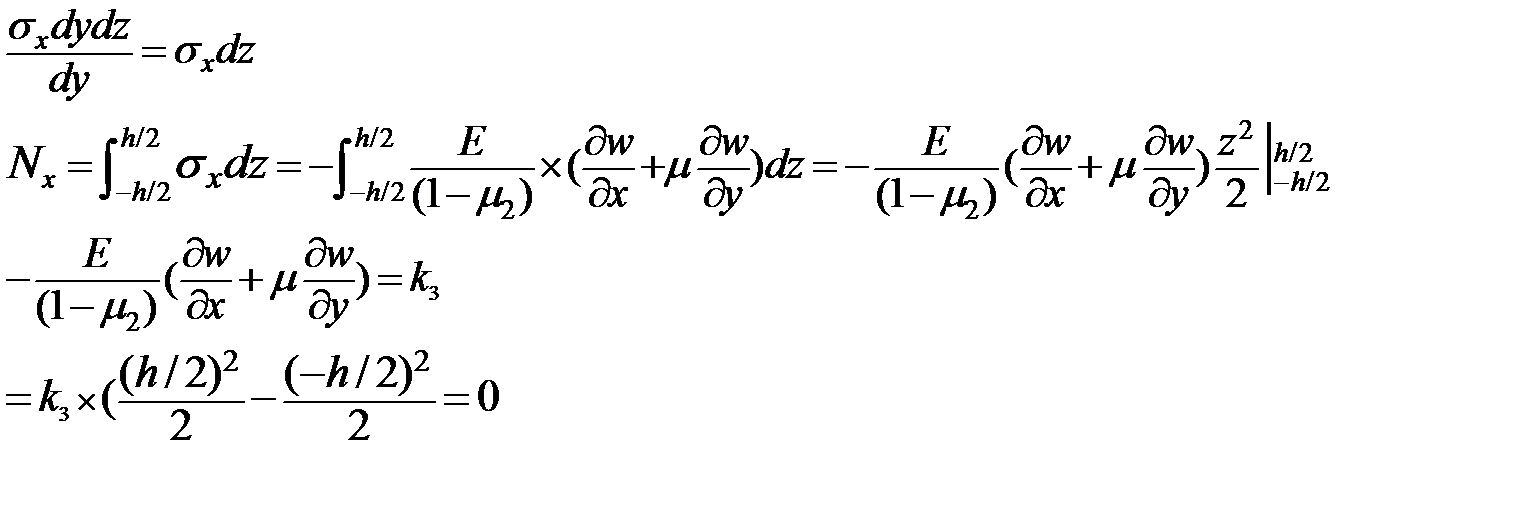
Нормальной силы в этом сечении не возникает. (сука а нахуя я тогда все это писал)
Найдем изгибающий момент:
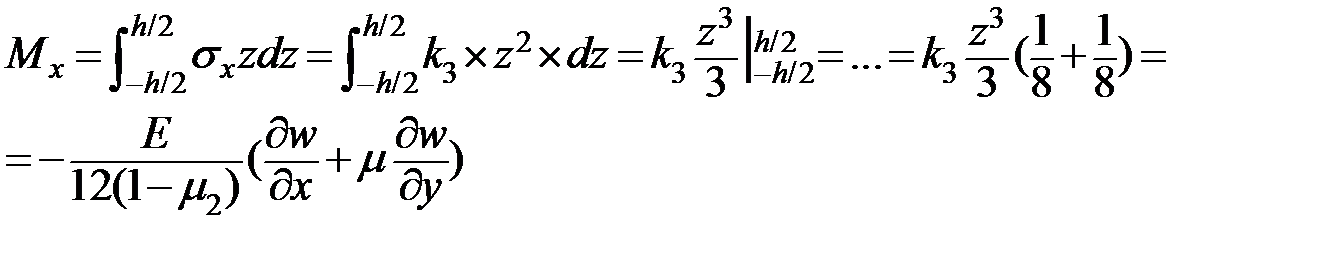
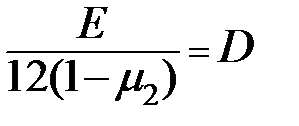- цилиндрическая жесткость при изгибе.
Поперечная сила:
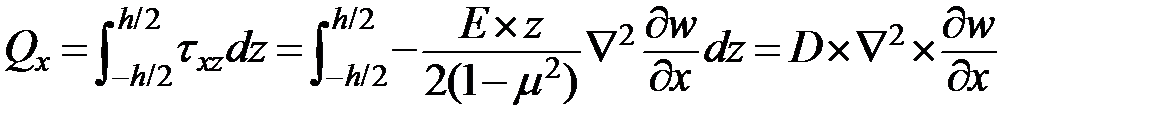
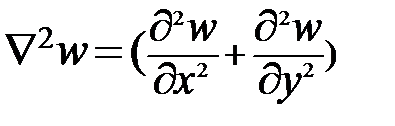
Сдвигающая сила
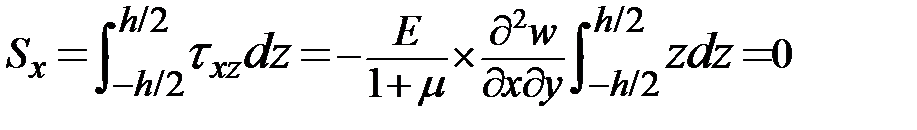
Погонный крутящий момент:
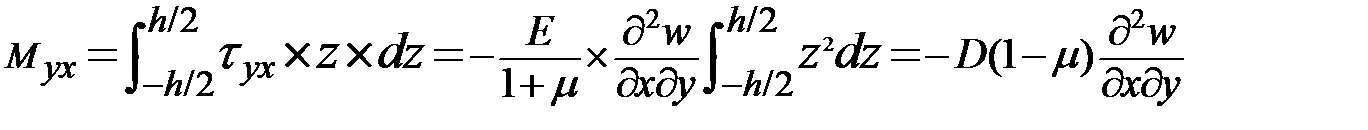
Аналогично найдем усилия, действующие в сечении с нормалью у.
Выражение напряжений через усилия
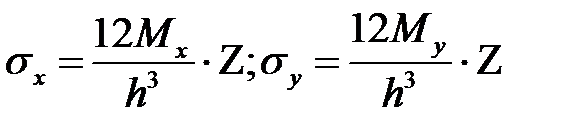
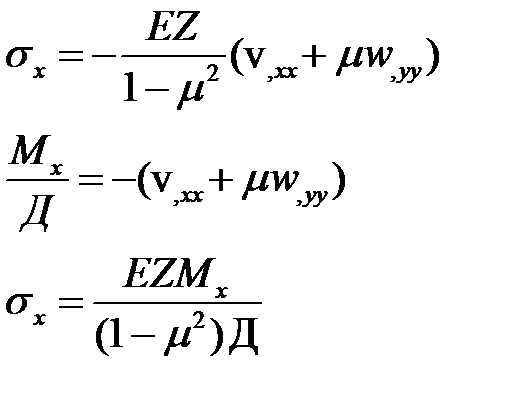
Нормальные напряжения при изгибе прямоугольной балки высотой h и шириной =1.
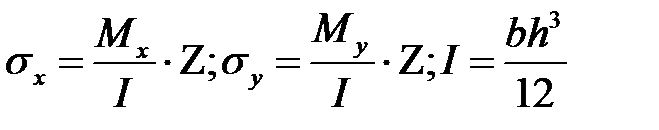
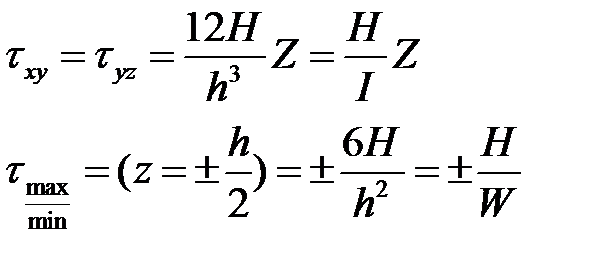
H-крутящий момент
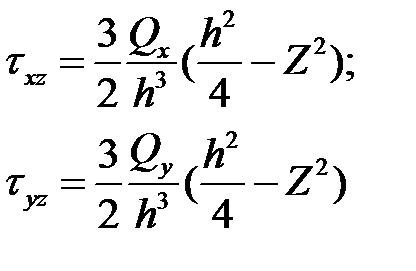
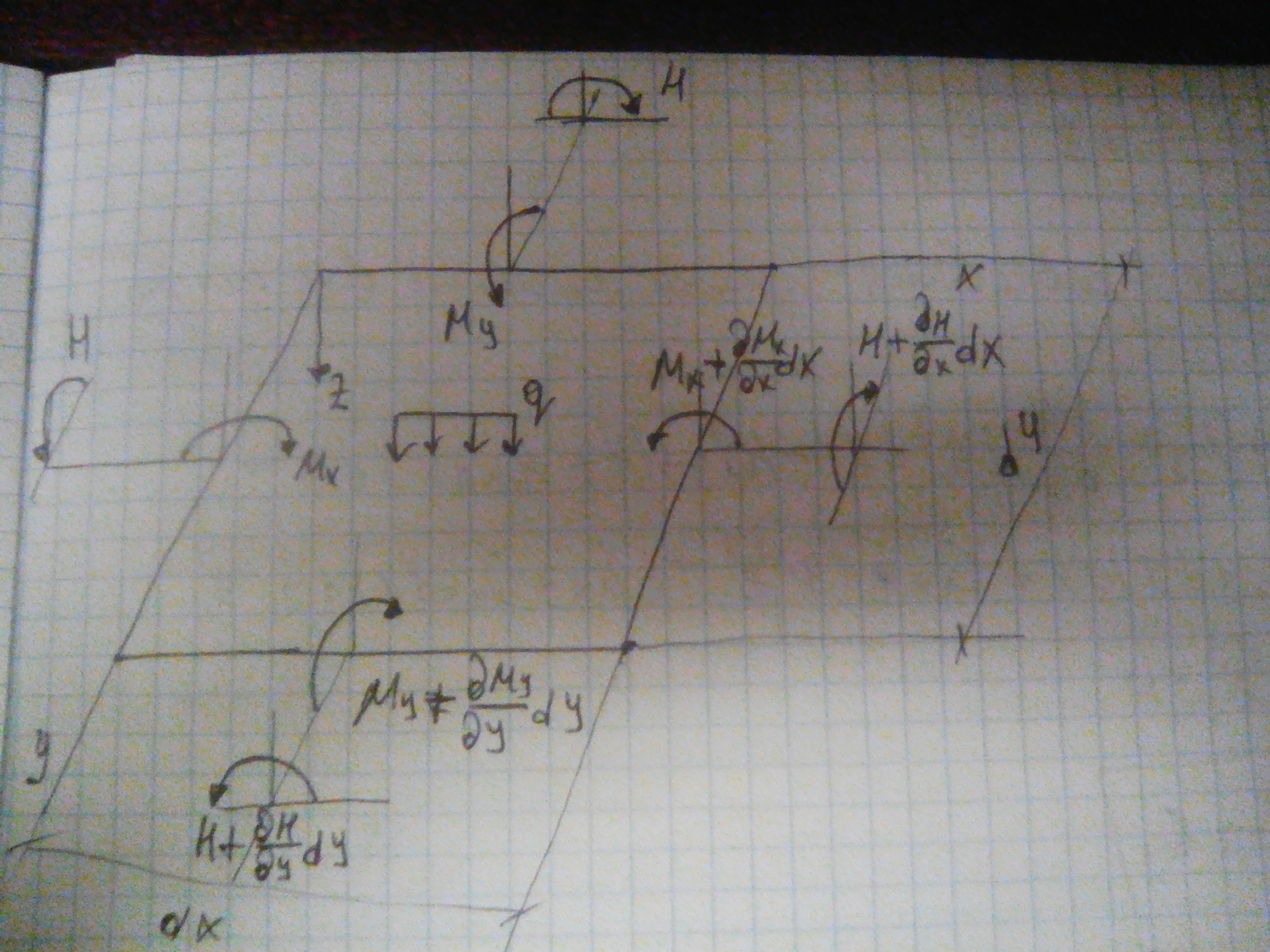
Уравнения равновесия элемента пластины
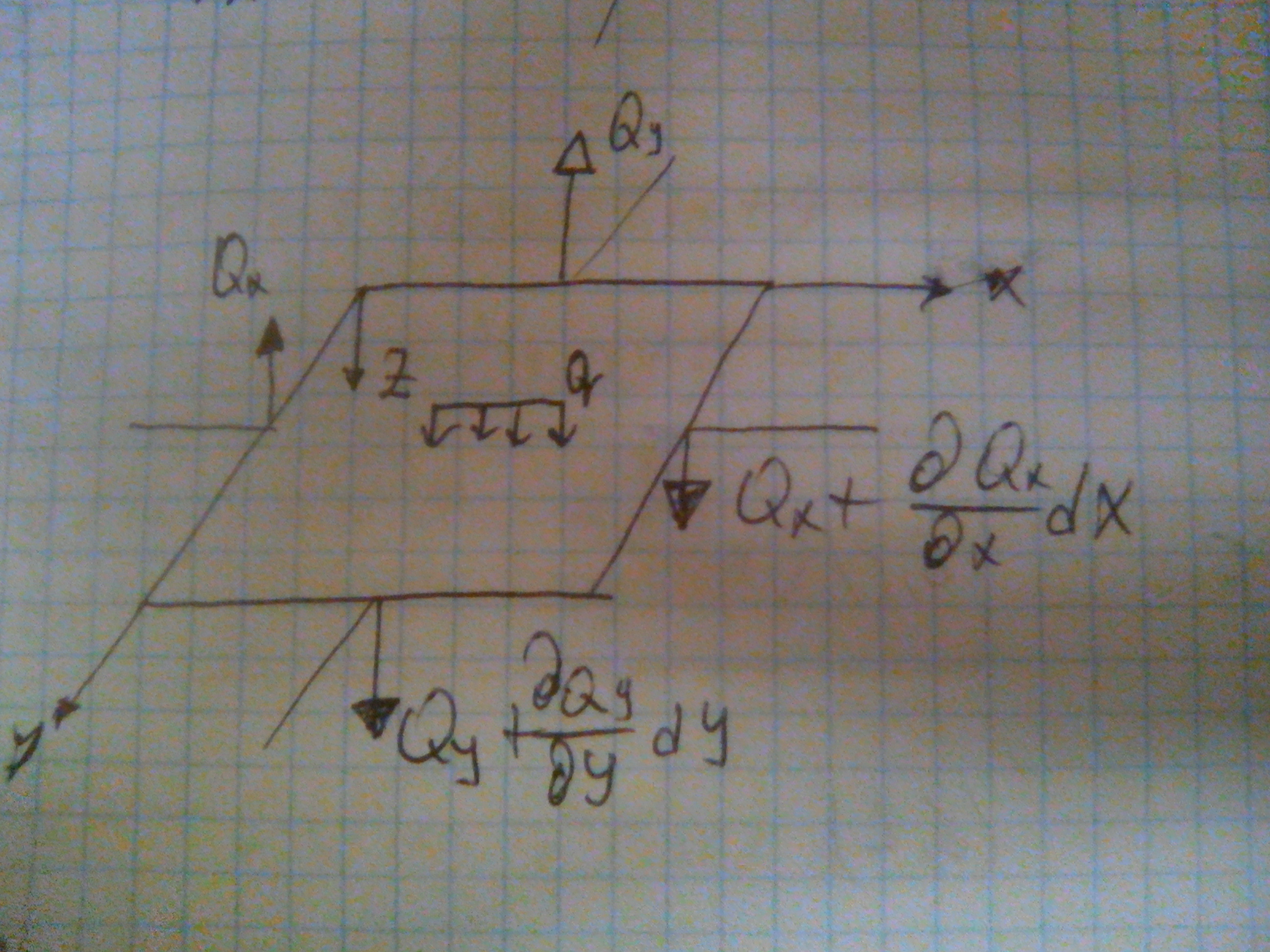
Спроекцируем все силы на ось Z.
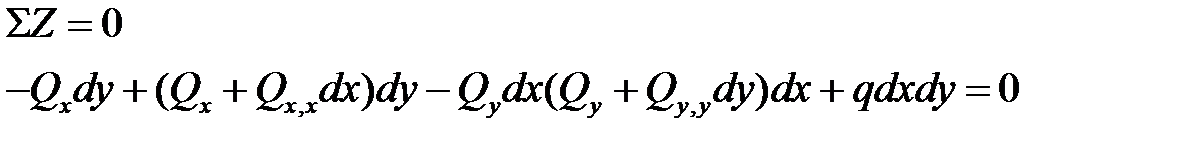
Приведя подобные члены:
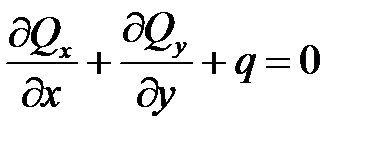
Запишем уравнение равновесия 
относительной ОХ.
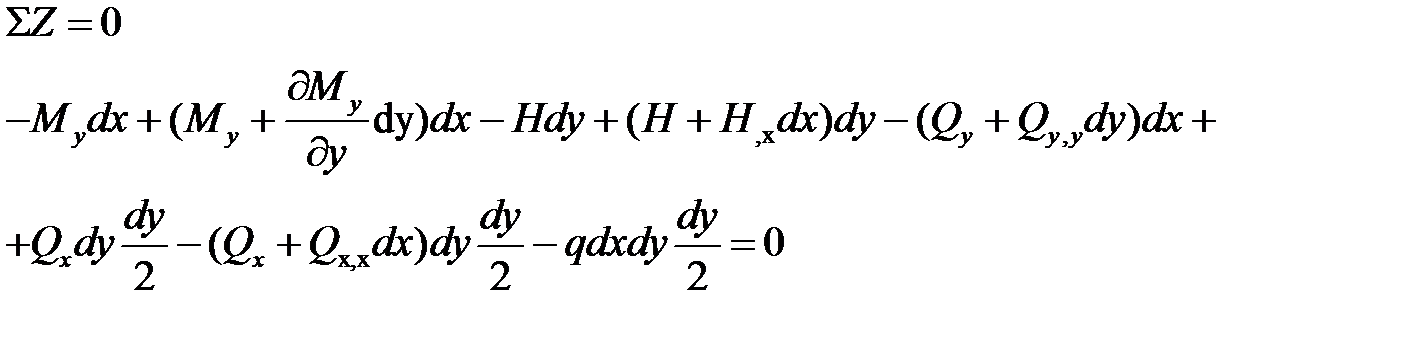
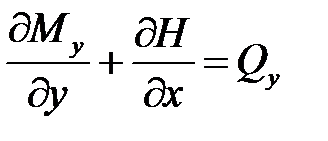
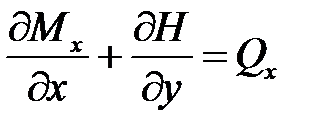
Граничные условия
Рассмотрим постановку граничных условий опирания пластинки и их выражения для функции прогиба.
Для начала рассмотрим эти условия для граней пластинки параллельных осям прямоугольной системы координат.
| a |
| б |
| Свободный край |
| Шарнирное опирание |
| Жесткая заделка |
| х |
| у |
| Рис. 4.1. Опирание пластинки |
Любой край пластинки может иметь как однородные (неизменные) условия опирания, так различные условия опирания на частях края. Варианты стандартного опирания пластинки приведены на рис. 4.1,6. В плане пластинки шарнирное опирание обозначается пунктиром (рис. 4.1,б).
а/. При заделке в сечении х=х0=const равны нулю прогиб и угол поворота по оси х равны нулю –
; 
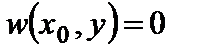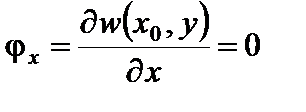. (4.1,а)
Аналогично при заделке в сечении у=у0, получаем
; 
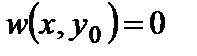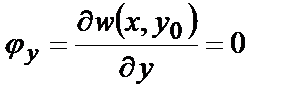. (4.1,б)
б/. При шарнирном опирании в сечении х=х0=const равны нулю прогиб и изгибающий момент.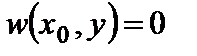 
; 
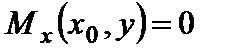. С учетом формул (2.1) из второго условия имеем 
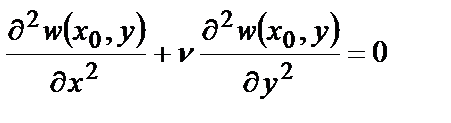. Но из условия 
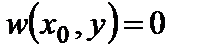следует, что 
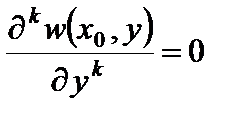. Следовательно, окончательно получаем условие шарнирного опирания в сечении х=х0:
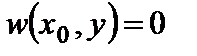и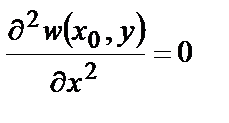 
. (4.2,а)
Аналогично, при шарнирном опирании в сечении у=у0=const :
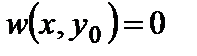и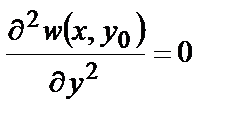 
. (4.2,б)
в/. Рассмотрим условия опирания свободного от закреплений края. Очевидно, что все напряжений на этом краю равны нулю и, следовательно, равны нулю все виды равнодействующих напряжений :
; 
; 
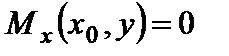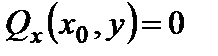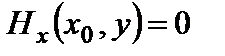. (4.3)
Таким образом на свободном краю мы получили 3 граничных условия. Но, решение дифференциального уравнения 2-го порядка позволяет удовлетворять только по 2 граничных условия. Это противоречие связано с гипотезами Кирхгофа, позволившим построить приближенную теорию изгиба пластин.
Чтобы обойти противоречие, на свободном краю вводят понятие обобщенной поперечной силы, являющейся комбинацией поперечной силы и крутящего момента. Для этого крутящие моменты Hdy и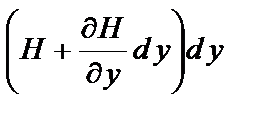 
на соседних малых элементах dx (в сечении х=х0=const) заменяют парами сил H и 
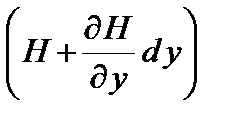. Суммируя вектора пар сил на границе дух элементов приводим действие крутящих моментов к эквивалентной поперечной силе 
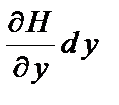(рис. 4.2).
Суммируя поперечную силу Qx и приведенную поперечную силу от крутящего момента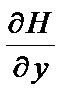 
(на единицу длины сечения) получаем обобщенную поперечную силу в сечении 
.
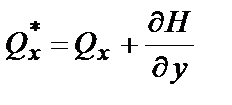| Рис. 4.2. Приведение крутящего момента к эквивалентной поперечной силе |
| dy |
| dy |
| y |
| Hdy |
 |
| = |
 |
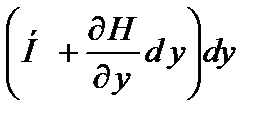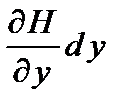| y |
| y |
 |
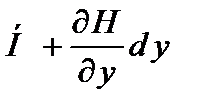| dy |
| dy |
| H |
| = |
Аналогично в сечении у=у0=const -
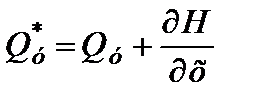. С учетом формул (4.1) (4.5). получим: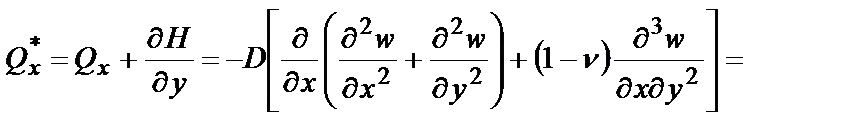 
;
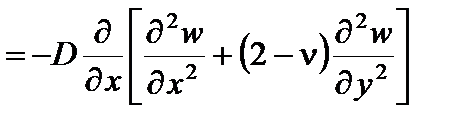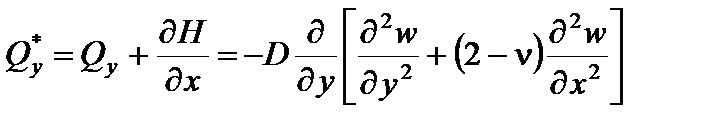. (4.4)
Граничные условия на свободных от закреплении краях получаем, приравнивая нулю изгибающий момент и обобщенную поперечную силу. В сечении х=х0=const
® 
; ® 
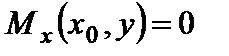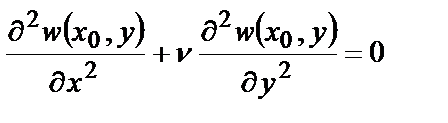
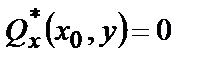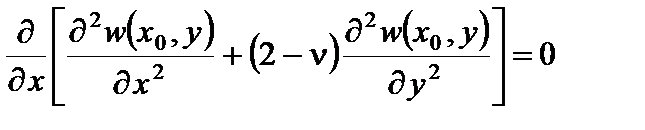. (4.5,а)
В сечении у=у0:
® 
; ® 
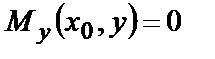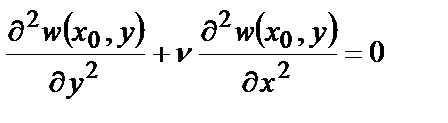
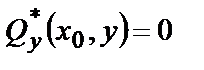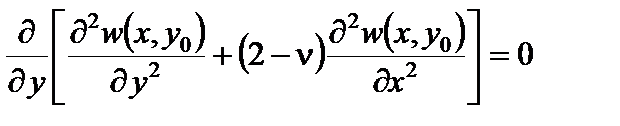. (4.5,б)
Использование обобщенной поперечной силы допустимо в рамках используемой приближенной теории. В реальной же пластинке при обобщенной силе равной нулю не означает равенства нулю каждого из слагаемых – поперечной силы и крутящего момента. Следовательно мы получаем на свободной кромке x=const решение с некоторой системой касательных напряжений tzх (соответственно Qx) и tyх (соответственно H). Эти усилия уравновешены в сечении и, согласно принципу Сен-Венана, им отвечает дополнительное поле напряжений, быстро затухающее при удалении от кромки в глубь пластинки и не влияющие на напряженной состояние в основной части пластинки.
| Рис. 4.3. |
| H |
| x |
| y |
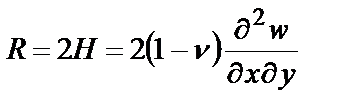. (4.6)
Если кромки пластинки сходятся в угловой точке под углом, отличным от 90°, то значение силы R будет зависеть от угла между кромками.
Расчет пластин МКЭ.
1 этап. Составление КЭ схемы:
a) выбор типа КЭ ( по геометрии, виду апроксимации ……..)
б) Разбивка области на КЭ с номерами узлов и элем.
В) Описание заданных узловых нагрузок
2 этап. Формирование матриц жёсткости и вектора узловых сил.
а) Составление элементов МЖ и ВН в локальной системе координат
б) Преобразование элементов МЖ и ВН из локальной в глобальную систему координат
3 этап. Учёт заданных статических и кинематических граничных условий.
Основные понятия, гипотезы, принимаемые при расчете пластин и следствия из них.
Пластиной называется призматическое тело, высота которого мала по сравнению с размерами в плане.
Плоскость которая делит пластину пополам называется срединной.
Линия пересечения бок. Пов. Пластинки со сред назю контуром пластины.
1) Толстые – пластины при b/h < =8….10. Расчёт производят как массивный объект.
2) Тонкие – 8….10<=b/h<=80….100
А)Жёсткие –w/h<=0.2…..0.5
Б)Гибкие- w/h > 0.2….0.5, работая на изгиб как мембрана.
3)Мембраны – b/h>=80…..100. Работаю только по закреп краям контура. Сопр на изгиб малы.
I) Гипотеза прямых номарлей.Любой линейный элемент, нормальный к срединной плоскости пластинки, остаётся прямолинейным и нормальным к срединной поверхности в процессе изгиба и длина не измен.
II) Отсутствет давление между слоями пластинки – напряжение надавливания горизонтальных слоёв пластинки друг на друга (сигма z) опускаем по сравнению с уровнями напряжений (сигма х, сигма y) . ГИПОТЕЗЫ КИРГОФА-ЛЯВА.
III) Нерастяжимости срединной поверхности – при малых прогибах (w/h <= 0,2….0,5) в срединной поверхности отсутств деформации напряжения, сжатия и сдвига нейтральна.
Выражение перемещений и деформаций через прогибы пластины
Первое допущение – длина перпендикуляра mn не измен. Т.к. 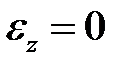и он не искривляется при изгибе ( )
------ ----
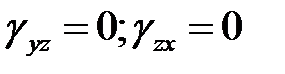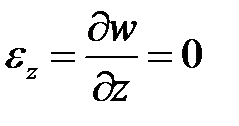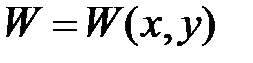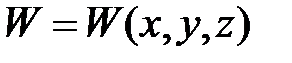
Ур-е говорит, что прогибы не зависят от Z и все точки принадлежат mn, получаем одинаковый прогиб.
Из ур-я КОШИ -----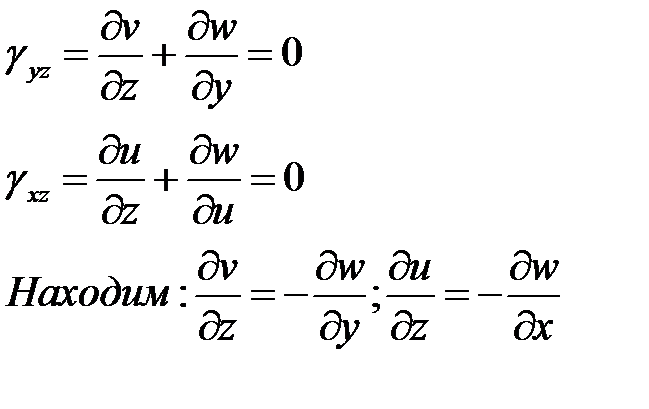
Интегрируя по Z получаем:
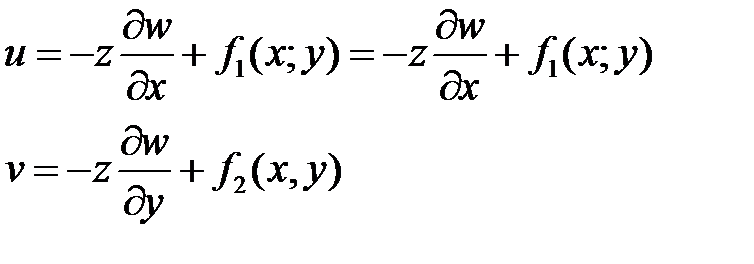
Пользуясь гипотезой нерастяжимости срединной плоскост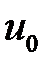и и 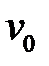при Z=0 равны 0.
Подставляя в ур-я получаем