Результаты моделирования и анализ полученных на модели результатов

Оптимальными параметрами исследу­емой системы, при которых максимальные гарантированные зат­раты на содержание склада минимальны, являются: объем партии товара и критический уровень запаса товара.

Приведем два варианта расчетов показателей системы.

Вариант 1.

• начальный уровень запаса товара N_УР = 1000;

• средний ежедневный спрос товара М_Д = 100;

• среднее квадратическое отклонение ежедневного спроса = 10;

• среднее время поставки партии товара М_Т = 3 дня;

• среднее квадратическое отклонение времени поставки товара
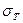= 1день;

• стоимость хранения единицы товара в течение суток С₁ = 2$

• стоимость поставки единицы товара С₂ = 1$;

• затраты на компенсацию отсутствия единицы товара на складе С₃= 10$;

• период функционирования склада T_D = 30 дней;

• число случайных реализаций N_P = 2000. Варьируемые переменные:

• объем партии товара Part = 40; 120; 200.

• уровень запаса, при котором должна оформляться заявка на поставку дополнительной партии товара UR_min = 50; 150; 250.

Результаты моделирования представлены в табл. 1.

Таблица 1. Зависимость максимальных гарантированных затрат от варьируемых переменных.

Part	URmin

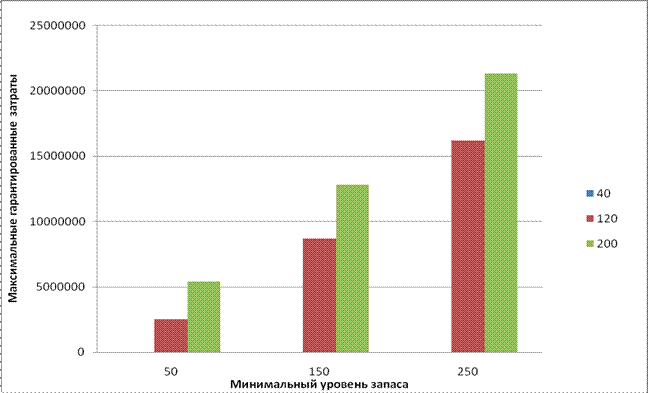
Диаграмма 1. Зависимость максимальных гарантированных затрат от варьируемых переменных.

Объем партии товара

Вариант 2.

• начальный уровень запаса товара N_УР = 500;

• средний ежедневный спрос товара М_Д = 60;

• среднее квадратическое отклонение ежедневного спрос = 10;

• среднее время поставки партии товара М_Т = 3 дня;

• среднее квадратическое отклонение времени поставки товара
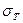= 1день;

• стоимость хранения единицы товара в течение суток С₁ = 2$

• стоимость поставки единицы товара С₂ = 1$;

• затраты на компенсацию отсутствия единицы товара на складе С₃= 10$;

• период функционирования склада T_D = 40 дней;

• число случайных реализаций N_P = 750. Варьируемые переменные:

• объем партии товара Part = 50; 100; 150.

• уровень запаса, при котором должна оформляться заявка на поставку дополнительной партии товара UR_min = 100; 200; 300.

Результаты моделирования представлены в табл. 2.

Таблица 2. Зависимость максимальных гарантированных затрат от варьируемых переменных.

Part	URmin

Диаграмма 2. Зависимость максимальных гарантированных затрат от варьируемых переменных.

Объем партии товара

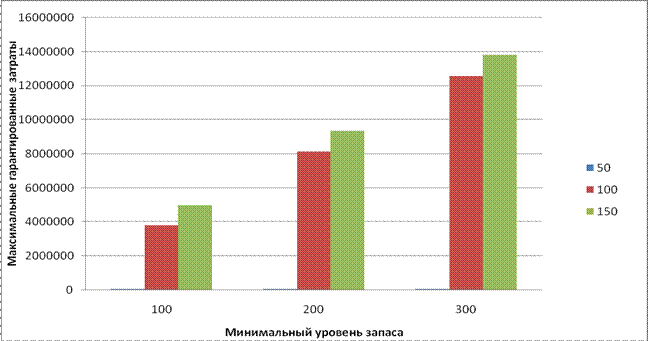
В приведенных решениях определяется параметр «Максимальные гарантированные расходы». Данный параметр показывает, при каком оптимальном уровне запаса UR_min, и оптимальном объем партии товара Part будут минимальны максимальные гарантированные затраты на содержание склада (с заданным уровнем гарантии). В качестве критерия выбора оптимального режима работы склада принимается минимум максимальных гарантированных затрат.

Заключение

В рамках данного курсового проекта было проведено ознакомление с современными подходами и методами создания и использования модели управления запасами. На основании изученных в теоретическом курсе методов моделирования была выбрана оптимальная по ряду параметров модель, рассмотрены все основные этапы с последующим анализом.

С помощью среды Visual Basic 6.0 был создан исполняемый модуль прог­раммы «Модель управления запасами», проведена отладка программы с целью ликвида­ции формальных ошибок и проведена проверка программы расчетом. Выполнено исследование закономерностей функционирования фирмы с помощью имитационной модели.

Данный модуль может применяться для минимизации затрат на содержание склада в течение определенного периода времени.

Задача является актуальной для всех предприятий, имеющий склад временного хранения товаров, так как управление складом сопряжено с рядом проблем, таких как содержание товара, определение критического количества и время и размер поставки новой партии.

Список используемой литературы

1. Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем: практикум. – М.: Финансы и статистика, 2000.

2. Лабскер Л.Г. и др. Математическое моделирование финансово-экономических ситуаций с применением компьютера. – М.: МЭСИ, 1998.

3. Романцев В.В., Яковлев С.А. Моделирование систем массового обслуживания. – СПб.: Изд. ЭТУ, 1993.

4. Фомин Г.П. Системы и модели массового обслуживания в коммерческой деятельности: Учебное пособие. – М.: Финансы и статистика, 2000.

5. Четыркин Е.М. Теория массового обслуживания и ее применение в экономике. – М.: Статистика, 1971.