Описание концептуальной модели

Модель является алгоритмической, то есть в ней критерии и ограничения описываются математическими конструкциями, включающими логические условия, приводящие к разветвлению вычислительного процесса. К алгоритмическим моделям относятся моделирующие алгоритмы, имитирующие поведение элементов изучаемого объекта и взаимодействие между ними в процессе функционирования.

Все алгоритмические, в том числе и имитационные, модели представляют собой модели типа «черного ящика». Алгоритмические модели не способны формировать свое собственное решение в том виде, в каком это имеет место в аналитических моделях, а могут лишь служить в качестве средства для анализа поведения системы в условиях, которые определяются пользователем. Это означает, что они обеспечивают расчет значений выходных характеристик при наличии на входе модели всей необходимой информации.

Свойства конкретной алгоритмической модели, на которых базируется алгоритм поиска оптимальных решений, например ее линейность или выпуклость, могут быть определены только в процессе экспериментирования с ней, в связи с чем для решения моделей этого класса используются методы экспериментальной оптимизации на ЭВМ.

Имеется склад, где хранится запас однотипного товара. На­чальный уровень запаса равен 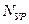. В результате удовлетворения ежедневного спроса происходит уменьшение запаса на случай­ную величину, имеющую нормальное распределение с известны­ми характеристиками: математическим ожиданием М_Д и средним квадратическим отклонением 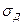. Затраты на хранение единицы товара в течение суток составляют $С₁.

Если на складе не останется товара, то администрации склада придется уплатить прибывшим покупателям компенсацию в раз­мере $С₃ за каждую недостающую единицу товара по отношению к заказанному количеству.

Чтобы избежать затрат, вызванных дефицитом товара, адми­нистрация склада периодически подает заявки на поставку до­полнительных партий товара выбранного объема Part. Подача за­явки производится в момент, когда уровень запаса товара снизит­ся до выбранного уровня UR_min. Время выполнения заявки явля­ется случайной величиной с нормальным распределением и изве­стными характеристиками М_Т и s_T. Затраты на поставку единицы товара составляют $С₂. Цикл работы склада составляет T_D дней.

Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы склада, обеспечивающий минимальные затраты на его содержа­ние.

Ø В частности, требуется установить:

Ø оптимальный уровень запаса UR_min, при достижении которо­го необходимо подавать заявку на поставку партии товара;

Ø оптимальный объем партии товара Part.

В качестве показателя эффективности моделируемого про­цесса целесообразно выбрать максимальные гарантированные затраты на содержание склада (с заданным уровнем гарантии), определяемые по формуле

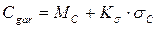
где М_с – средние затраты на содержание склада в течение периода T_D дней;

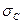– среднее квадратическое отклонение затрат на содержание склада;
К_а – квантиль, зависящий от уровня гарантии а (К_а = 1,28 при а = 0,9).

В качестве критерия выбора оптимального режима работs склада может быть принят минимум максимальных гарантированных затрат:

,

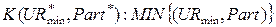где 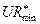– оптимальное значение уровня запаса товара, при достижении которого необходимо подавать заявку на поставку новой партии; Part – оптимальный объем партии товара.

Затраты на склад включают:

• стоимость хранения единицы товара в течение суток – $С₁;

• стоимость поставки единицы товара – $С₂;

• стоимость затрат на компенсацию отсутствия товара на складе – $С₃ за каждую недостающую единицу;

В состав базового комплекта исходных данных также входят:

• начальный уровень запаса товара – ;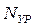

• средний ежедневный спрос товара – М_Д;

• среднее квадратическое отклонение ежедневного спроса –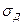

• объем партии товара -Part;

• уровень запаса, при котором должна оформляться заявка на поставку дополнительной партии товара – UR_min;

• среднее время поставки партии товара – М_Т дней;

• среднее квадратическое отклонение времени поставки товара – 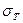дней;

• период функционирования склада – T_D дней;

• число случайных реализаций — N_Р.

Решением задачи является функция

Затраты на содержание склада=($С₁₊$С₂₊$С₃ )→min

при UR_min <Текущем объеме товара<Объем товара, при котором будут увеличиваться затраты на содержание склада