Особенности и методы создания модели управления запасами
ФГОУ ВПО
«КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ФГОУ ВПО
«Калининградский государственный технический университет»
Кафедра систем управления и вычислительной техники
Рекомендована к защите: Защищена с оценкой:
___________________ ____________________
дата, подпись дата, подпись
Пояснительная записка
к курсовой работе по Моделированию Экономических Процессов (МЭП)
Вариант 9
Особенности и методы создания модели управления запасами
Работу выполнили:
студенты группы 06-ИЭ
Леонидов Д.В.
Денисова Е. И.
Работу проверил:
Д.т.н., проф.
Арунянц Г.Г.
Калининград – 2009
Аннотация
Основной целью курсовой работы является ознакомление с современными подходами и методами создания и использования модели управления запасами.
В задании приводятся результаты разработки модели бензоколонки с использованием исходных данных, формируемым в результате предварительных исследований, представленных в форме беседы предпринимателя с консультантом (разработчиком). Такая форма представления материала предполагает более доходчивое понимание самой сути и содержания основных этапов построения модели, включая рассмотрение всех основных этапов, и ее использования для последующего анализа.
Необходимым условиям успешного выполнения задания являются базовые знания использования языка Visual Basic 6.0.
Бланк задания
Имеется склад, где хранится запас однотипного товара. Начальный уровень запаса равен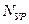 
. В результате удовлетворения ежедневного спроса происходит уменьшение запаса на случайную величину, имеющую нормальное распределение с известными характеристиками: математическим ожиданием МД и средним квадратическим отклонением 
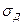. Затраты на хранение единицы товара в течение суток составляют $С1.
Если на складе не останется товара, то администрации склада придется уплатить прибывшим покупателям компенсацию в размере $С3 за каждую недостающую единицу товара по отношению к заказанному количеству.
Чтобы избежать затрат, вызванных дефицитом товара, администрация склада периодически подает заявки на поставку дополнительных партий товара выбранного объема Part. Подача заявки производится в момент, когда уровень запаса товара снизится до выбранного уровня URmin. Время выполнения заявки является случайной величиной с нормальным распределением и известными характеристиками МТ и sT. Затраты на поставку единицы товара составляют $С2. Цикл работы склада составляет TD дней.
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы склада, обеспечивающий минимальные затраты на его содержание.
Содержание
Аннотация……………………………………………………………………………..2
Бланк задания………………………………………………………………………….3
Введение……………………………………………………………………………….5
1. Формулировка проблемы…………………………………………………………7
2. Аналитический обзор возможностей исследования проблемы оптимизации склада………………………………………………………………………………8
3. Обоснование выбранного подхода к моделированию………………………….9
4. Описание концептуальной модели………………………………………………10
5. Формализация и алгоритмизация модели……………………………………….11
6. Описание алгоритмов и программ……………………………………………….12
7. Инструкции по использованию программ при моделировании на конкретной ЭВМ………………………………………………………………………………..19
8. Результаты моделирования и анализ полученных на модели результатов….20
Заключение…………………………………………………………………………….23
Список используемой литературы…………………………………………………...24
Введение
В рамках данной курсовой работы планируется разработать модель процесса работы склада.
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы склада, обеспечивающий минимальные затраты на его содержание.
Задача заключается в создании алгоритмической модели процесса функционирования сложной системы с целью оптимизации ее параметров. В данном случае условием оптимальности будет условие минимизации затрат на содержание склада в течение определенного периода времени.
Задача является актуальной для всех предприятий, имеющий склад временного хранения товаров, так как управление складом сопряжено с рядом проблем, таких как содержание товара, определение критического количества и время и размер поставки новой партии.
Решить задачу предполагается путем создания «Модели управления запасами».
В процессе решения поставленной задачи были изучены следующие дополнительные материалы :
1.Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем: практикум. – М.: Финансы и статистика, 2000.
2.Лабскер Л.Г. и др. Математическое моделирование финансово-экономических ситуаций с применением компьютера. – М.: МЭСИ, 1998.
3.Романцев В.В., Яковлев С.А. Моделирование систем массового обслуживания. – СПб.: Изд. ЭТУ, 1993.
4.Фомин Г.П. Системы и модели массового обслуживания в коммерческой деятельности: Учебное пособие. – М.: Финансы и ста-тистика, 2000.
5.Четыркин Е.М. Теория массового обслуживания и ее применение в экономике. – М.: Статистика, 1971.
Цель моделирования экономических процессов состоит в получении устойчивой схемы, позволяющей обеспечить качество управления маркетинговой системы, поскольку последовательность оказываемых услуг повторяется. Важной процедурной концепцией анализа эффективности является определение критического количества продукции на складе.
Полученное с помощью модели конкретное оптимальное решение является наилучшим только в рамках использования именно этой модели. Другими словами, оно является наилучшим из всех возможных только тогда, когда выбранный критерий оптимизации можно считать полностью адекватным целям организации, в которой возникла исследуемая проблемная ситуация.
Формулировка проблемы
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наиболее выгодный режим работы склада, обеспечивающий минимальные затраты на его содержание.
Нужно установить, каким должно быть оптимальное количество автомашин, хранящихся на складе. Количество покупателей, приобретающих товар каждый день, заранее неизвестно. Его можно только ориентировочно оценить. Поэтому неопределенным является и минимальный запас, который нужно поддерживать на складе ежедневно. С одной стороны, с увеличением запаса товара растут эксплуатационные расходы. С другой стороны, при уменьшении запаса товара может возникнуть ситуация, при которой некоторые покупатели, оформившие покупку, не смогут получить товар к концу рабочего дня. В этом случае нужно выплачивать покупателям неустойку в довольно крупных размерах. В то же время организация подвоза новых партий товара требует нескольких дней и сопряжена с дополнительными затратами.
Стоимость затрат на хранение товара пропорциональна количеству автомашин, находящихся на складе в данный день. Стоимость затрат на доставку товара пропорциональна объему партии. Стоимость затрат, вызванных дефицитом товара, пропорциональна количеству покупателей, спрос которых остался неудовлетворенным.
Заключение
В рамках данного курсового проекта было проведено ознакомление с современными подходами и методами создания и использования модели управления запасами. На основании изученных в теоретическом курсе методов моделирования была выбрана оптимальная по ряду параметров модель, рассмотрены все основные этапы с последующим анализом.
С помощью среды Visual Basic 6.0 был создан исполняемый модуль программы «Модель управления запасами», проведена отладка программы с целью ликвидации формальных ошибок и проведена проверка программы расчетом. Выполнено исследование закономерностей функционирования фирмы с помощью имитационной модели.
Данный модуль может применяться для минимизации затрат на содержание склада в течение определенного периода времени.
Задача является актуальной для всех предприятий, имеющий склад временного хранения товаров, так как управление складом сопряжено с рядом проблем, таких как содержание товара, определение критического количества и время и размер поставки новой партии.
Список используемой литературы
1. Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем: практикум. – М.: Финансы и статистика, 2000.
2. Лабскер Л.Г. и др. Математическое моделирование финансово-экономических ситуаций с применением компьютера. – М.: МЭСИ, 1998.
3. Романцев В.В., Яковлев С.А. Моделирование систем массового обслуживания. – СПб.: Изд. ЭТУ, 1993.
4. Фомин Г.П. Системы и модели массового обслуживания в коммерческой деятельности: Учебное пособие. – М.: Финансы и статистика, 2000.
5. Четыркин Е.М. Теория массового обслуживания и ее применение в экономике. – М.: Статистика, 1971.
ФГОУ ВПО
«КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ФГОУ ВПО
«Калининградский государственный технический университет»
Кафедра систем управления и вычислительной техники
Рекомендована к защите: Защищена с оценкой:
___________________ ____________________
дата, подпись дата, подпись
Пояснительная записка
к курсовой работе по Моделированию Экономических Процессов (МЭП)
Вариант 9
Особенности и методы создания модели управления запасами
Работу выполнили:
студенты группы 06-ИЭ
Леонидов Д.В.
Денисова Е. И.
Работу проверил:
Д.т.н., проф.
Арунянц Г.Г.
Калининград – 2009
Аннотация
Основной целью курсовой работы является ознакомление с современными подходами и методами создания и использования модели управления запасами.
В задании приводятся результаты разработки модели бензоколонки с использованием исходных данных, формируемым в результате предварительных исследований, представленных в форме беседы предпринимателя с консультантом (разработчиком). Такая форма представления материала предполагает более доходчивое понимание самой сути и содержания основных этапов построения модели, включая рассмотрение всех основных этапов, и ее использования для последующего анализа.
Необходимым условиям успешного выполнения задания являются базовые знания использования языка Visual Basic 6.0.
Бланк задания
Имеется склад, где хранится запас однотипного товара. Начальный уровень запаса равен 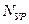. В результате удовлетворения ежедневного спроса происходит уменьшение запаса на случайную величину, имеющую нормальное распределение с известными характеристиками: математическим ожиданием МД и средним квадратическим отклонением 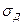. Затраты на хранение единицы товара в течение суток составляют $С1.
Если на складе не останется товара, то администрации склада придется уплатить прибывшим покупателям компенсацию в размере $С3 за каждую недостающую единицу товара по отношению к заказанному количеству.
Чтобы избежать затрат, вызванных дефицитом товара, администрация склада периодически подает заявки на поставку дополнительных партий товара выбранного объема Part. Подача заявки производится в момент, когда уровень запаса товара снизится до выбранного уровня URmin. Время выполнения заявки является случайной величиной с нормальным распределением и известными характеристиками МТ и sT. Затраты на поставку единицы товара составляют $С2. Цикл работы склада составляет TD дней.
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы склада, обеспечивающий минимальные затраты на его содержание.
Содержание
Аннотация……………………………………………………………………………..2
Бланк задания………………………………………………………………………….3
Введение……………………………………………………………………………….5
1. Формулировка проблемы…………………………………………………………7
2. Аналитический обзор возможностей исследования проблемы оптимизации склада………………………………………………………………………………8
3. Обоснование выбранного подхода к моделированию………………………….9
4. Описание концептуальной модели………………………………………………10
5. Формализация и алгоритмизация модели……………………………………….11
6. Описание алгоритмов и программ……………………………………………….12
7. Инструкции по использованию программ при моделировании на конкретной ЭВМ………………………………………………………………………………..19
8. Результаты моделирования и анализ полученных на модели результатов….20
Заключение…………………………………………………………………………….23
Список используемой литературы…………………………………………………...24
Введение
В рамках данной курсовой работы планируется разработать модель процесса работы склада.
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наивыгоднейший режим работы склада, обеспечивающий минимальные затраты на его содержание.
Задача заключается в создании алгоритмической модели процесса функционирования сложной системы с целью оптимизации ее параметров. В данном случае условием оптимальности будет условие минимизации затрат на содержание склада в течение определенного периода времени.
Задача является актуальной для всех предприятий, имеющий склад временного хранения товаров, так как управление складом сопряжено с рядом проблем, таких как содержание товара, определение критического количества и время и размер поставки новой партии.
Решить задачу предполагается путем создания «Модели управления запасами».
В процессе решения поставленной задачи были изучены следующие дополнительные материалы :
1.Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем: практикум. – М.: Финансы и статистика, 2000.
2.Лабскер Л.Г. и др. Математическое моделирование финансово-экономических ситуаций с применением компьютера. – М.: МЭСИ, 1998.
3.Романцев В.В., Яковлев С.А. Моделирование систем массового обслуживания. – СПб.: Изд. ЭТУ, 1993.
4.Фомин Г.П. Системы и модели массового обслуживания в коммерческой деятельности: Учебное пособие. – М.: Финансы и ста-тистика, 2000.
5.Четыркин Е.М. Теория массового обслуживания и ее применение в экономике. – М.: Статистика, 1971.
Цель моделирования экономических процессов состоит в получении устойчивой схемы, позволяющей обеспечить качество управления маркетинговой системы, поскольку последовательность оказываемых услуг повторяется. Важной процедурной концепцией анализа эффективности является определение критического количества продукции на складе.
Полученное с помощью модели конкретное оптимальное решение является наилучшим только в рамках использования именно этой модели. Другими словами, оно является наилучшим из всех возможных только тогда, когда выбранный критерий оптимизации можно считать полностью адекватным целям организации, в которой возникла исследуемая проблемная ситуация.
Формулировка проблемы
Требуется разработать математическую модель, которая бы описывала возможный реальный процесс, позволяла изучать его закономерности и выбирать наиболее выгодный режим работы склада, обеспечивающий минимальные затраты на его содержание.
Нужно установить, каким должно быть оптимальное количество автомашин, хранящихся на складе. Количество покупателей, приобретающих товар каждый день, заранее неизвестно. Его можно только ориентировочно оценить. Поэтому неопределенным является и минимальный запас, который нужно поддерживать на складе ежедневно. С одной стороны, с увеличением запаса товара растут эксплуатационные расходы. С другой стороны, при уменьшении запаса товара может возникнуть ситуация, при которой некоторые покупатели, оформившие покупку, не смогут получить товар к концу рабочего дня. В этом случае нужно выплачивать покупателям неустойку в довольно крупных размерах. В то же время организация подвоза новых партий товара требует нескольких дней и сопряжена с дополнительными затратами.
Стоимость затрат на хранение товара пропорциональна количеству автомашин, находящихся на складе в данный день. Стоимость затрат на доставку товара пропорциональна объему партии. Стоимость затрат, вызванных дефицитом товара, пропорциональна количеству покупателей, спрос которых остался неудовлетворенным.