Практическая задача № 2 линейной модели.

Назначение на должность

Постановка задачи.

Название задачи и соответственной модели – о назначении (assignment problem) – непосредственно исходить от практической кадровой ситуации, когда претендентов нужно назначить на вакантные должности наилучшим образом.
Критерий максимизации общего аффекта используется тогда, когда известны о каждом претенденте заданные оценки способности исполнения определенной функции (чем выше, тем лучше), минимизации – когда, скажем, для каждого претендента заданная величина затрат на его подготовку для определенной деятельности (чем выше, тем хуже).

Пример. Предприятие объявило набор работников для нового цеха – указало названия семи должностей и количество вакансий по каждой из них. Кадровая служба собрала от 18 претендентов на эти должности, провела тестирование по каждой из них и за результатами определила 5 групп с одинаковыми оценками и возможностями, получивши соответственную таблицу средних оценок их умений и знаний.
Нужно назначить на вакантные должности претендентов таким образом, что бы общая эффективность исполнения ними соответствующих обязанностей была максимальной.

Особенность – наличие высокой оценки еще не гарантирует успех, поскольку целью оптимизации о назначении есть максимальный общий эффект.
Экономико-математическая модель.

1. Найти такую матрицу назначений, чтобы

2. Общий эффект=Матрица_оценок*Матрица_назначений - mах

3. При ограничениях: Назначено<=Всего_претендентов;

Занято=Всего_вакансий.
Матрица_назначений>=0.
Реализация в Excel.

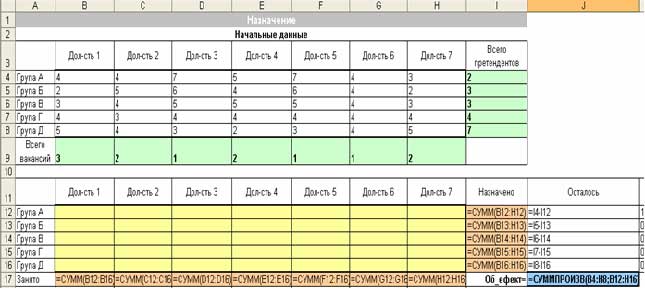Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Об_эффект):

· в столбец Назначено вводим формулу сумы по сроках матрицы назначено;

· в столбец Осталось вводим формулу Всего претендентов-Назначено;

· в строку Занято вводим формулу сумы по столбцах матрицы назначено;

· целевую ячейку заполняем формулой:

=СУММПРОИЗВ(Матрица_оценок; Матрица_назначений).

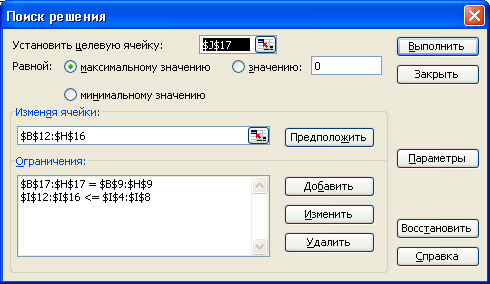
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить и в появившемся окне Результаты поиска решения выводим отчет по устойчивости.

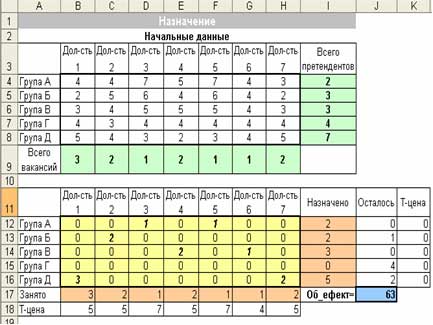
Анализ результатов.

Оптимальный план назначений (смотри таблицу) обеспечивает общую эффективность 63.

Теневые цены для претендентов показывают, на сколько изменится целевая ячейка при увеличении данного претендента на 1 ед. Теневые цены для вакансий показывают «ценность» соответствующих должностей.
Нормированные стоимости для нулевых назначений означают:

· на сколько нужно увеличить оценку, чтобы можно было претендовать на назначение;

· на сколько уменьшиться общая эффективность, если на должность будет назначен этот «невыгодный» претендент.

Заключение

Многие задачи, с которыми приходится сталкиваться экономисту в повседневной практике при анализе хозяйственной деятельности предприятий, многовариантны. Так как не все варианты одинаково хороши, среди множества возможных приходится отыскивать оптимальный. Значительная часть подобных задач на протяжении долгого времени решалась исходя из здравого смысла и опыта. При этом не было никакой уверенности, что найденный вариант является наилучшим.

В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием «оптимизационные методы анализа и принятия решения в экономике».

Чтобы решить экономическую задачу математическими методами, прежде всего необходимо построить адекватную ей математическую модель, т.е. формализовать цель и условия задачи в виде математических функций, уравнений и (или) неравенств.

Из данной курсовой работы стало ясно, что внедрение экономико-математических методов помогает совершенствовать анализ финансового-хозяйственной деятельности. Их применение повышает эффективность экономического анализа за счет расширения факторов, обоснования принимаемых управленческих решений, выбора оптимального варианта использования хозяйственных ресурсов, выявления и мобилизации резервов повышения эффективности производства.

Список используемой литературы:

1. Басовский Л.Е. Теория анализа хозяйственной деятельности. М.: ИНФРА-М, 2001г.

2. Савицкая Г. В. Экономический анализ. М.: Новое издание, 2004г.

3. Шеремет А. Д. Теория экономического анализа. М.: ИНФРА-М, 2002г

4. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем; Учебное пособие. – М.: Финансы и статистика. 2003. – 368 с.

5. Бережной В.И., Бережная Е.В. Экономико-математические методы и модели в примерах и задачах. – Ставрополь: Интеллект-сервис. 1996. – 188 с.

6. Советов Б.Я., Яковлев С.А. Моделирование систем:Учебное пособие для втузов – 3-е изд., перераб. и доп. – М.: Высшая школа, 2001. –343 с.

7. Белобродский-Гриценко. Поиск решений с Excel 2000 - Руководство по решению экстремальных задач в экономике - 2003 – 76 с.