Постановка задачи, условия и порядок применения

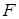-критерия Фишера

На практике задача сравнения дисперсий возникает, если требуется сравнить точность методов измерений, вариативность результатов и т.д. Очевидно, предпочтительнее тот метод, который обеспечивает наименьшую дисперсию результатов измерений.

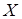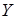Постановка задачи. Пусть генеральные совокупности и распределены по нормальному закону с предполагаемыми параметрам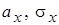и и 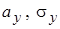. Требуется при заданном уровне значимости 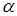проверить нулевую гипотезу, что генеральные дисперсии рассматриваемых совокупностей равны между собой. При проверке 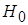значения 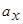и 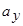несущественны и не представляют интереса.

Условия применения 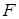-критерия Фишера

1.Измерения проведены в шкале интервалов и отношений.

2.Сравниваемые выборки независимы и распределены по нормальному закону.

Порядок действий

Шаг 1. Формулируются нулевая и альтернативная гипотезы.

Нулевая гипотеза .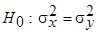

Альтернативная гипотеза .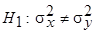

Шаг 2. Задается уровень значимости .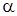

Шаг 3. По независимым выборкам объемов 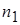и 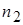вычисляются выборочные дисперсии:

; .

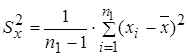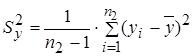Шаг 4. Вычисляется эмпирическое значение критерия

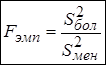(5.9)

– отношение большей выборочной дисперсии к меньшей выборочной дисперсии. Отсюда следует, что значение 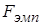всегда будет больше или равно единице: .

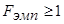Шаг 5. Для альтернативной гипотезы 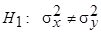критическая область двусторонняя. Ее границы определяются двумя числами, которые находятся по таблице и зависят от уровня значимости 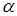и числа степеней свободы 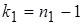(для большей дисперсии) и 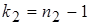(для меньшей дисперсии). Это числа

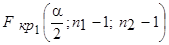и .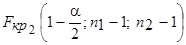

Правую точку 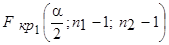в 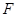-распределении можно определить непосредственно по таблице. Левая точка связана с правой следующим образом:

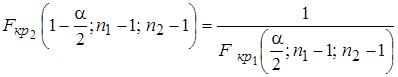. (5.10)

Шаг 6. Гипотеза 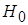о равенстве дисперсий принимается, если 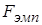попало в область допустимых значений

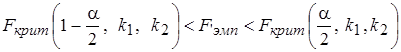. (5.11)

В этом случае делается вывод, что различие выборочных дисперсий незначимо и объясняется случайными причинами, в частности, случайным отбором объектов выборки.

Если нулевая гипотеза отвергнута, то можно утверждать, что различие выборочных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны.

Замечания.

1. Вопрос о том, какую выборку обозначать первым или вторым номером, обычно решается произвольно. В качестве первой выборки обычно берется та, для которой вычисленная выборочная дисперсия больше.

2. В прошлом было принято проверять гипотезу 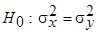до проверки по 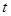-критерию гипотезы 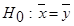. В учебниках советовали не приступать к испытанию по 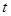-критерию, если отношение 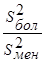привело к отклонению гипотезы о равенстве дисперсий. Однако это не так.

Более важным условием является нормальность совокупностей, поскольку отсутствие нормальности совокупностей не увеличивает обоснованности применения 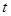-критерия. Но при отсутствии нормальности совокупностей проверка предположения об однородности дисперсий может оказаться необоснованной. Предположение об извлечении выборок из нормальной совокупности нельзя принять необдуманно в случае гипотез о генеральных дисперсиях, в отличие от проверки гипотез относительно средних по критерию Стьюдента [1, с. 276-278].

3. При равных объемах совокупностей 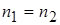нет оснований говорить о нарушении допущения об однородных дисперсиях. Однако если точно установлено, что совокупности описываются нормальным законом, а 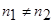, то стоит специально проверить гипотезу о равенстве дисперсий еще до проверки гипотезы о равенстве средних.

4. В случае зависимых выборок проверка гипотезы о равенстве дисперсий осуществляется с помощью другого критерия. Его описание можно найти в книге [1, с. 279].

2. Пример применения критерия 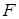- Фишера

Задача 3.При решении задачи об уровне интеллекта в двух группах по признаку 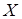«число правильных ответов на тестовые задания» выяснилось, что нет оснований для отклонения гипотезы о равенстве средних значений признака в двух группах. Однако психолога заинтересовал вопрос: есть ли различия в степени изменчивости показателей умственного развития между группами?

Решение

Получены следующие данные: в первой группе 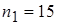, , 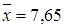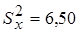; во второй группе , , .

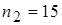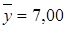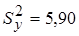Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в группах. Выдвинем нулевую гипотезу 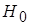о равенстве генеральных двух дисперсий, т.е. : .

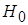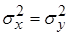Поскольку исследователя интересует только, имеются ли различия в степени изменчивости показателей, но не интересует, в какой группе она больше, то альтернативная гипотеза 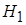: 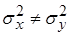, в этом случае критическая область двусторонняя. Уровень значимости принимаем 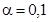; число степеней свободы равно , .

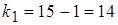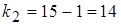По таблице распределения Фишера находим правую критическую точку 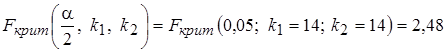. Тогда значение левой критической точки найдем по формуле (5.10):

.

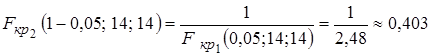Вычислим эмпирическое значение 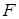-критерия

.

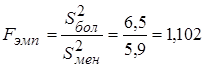Так как 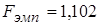удовлетворяет неравенству 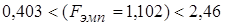, то 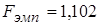попало в область допустимых значений. Значит, нет оснований на уровне значимости 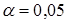отвергнуть нулевую гипотезу о равенстве дисперсий.

Психолог может утверждать, что нет различия между выборками из двух групп по степени изменчивости показателя «умственное развитие».