Лекция 8. Методы проверки статистических гипотез.

План:

1. Статистические гипотезы

2. Статистические критерии

3. Процедура проверки статистических гипотез

1.Статистические гипотезы

Любое исследование направлено на определение некоторой характеристики изучаемой генеральной совокупности или выявление связи между признаками (факторами). Такая связь часто исследуется в причинно-следственном аспекте, когда некоторые факторы рассматриваются как причины (независимые переменные), а другие - как следствия или результаты (зависимые переменные). Связь может характеризоваться не только величиной (степенью связи) и направлением (что показывает, например, коэффициент корреляции), но также и статистической достоверности. Последняя характеристика связи показывает, можно ли распространить результаты, полученные на данной выборке, на всю генеральную совокупность, из которой взята эта выборка.

Любое заключение, полученное из статистического наблюдения / исследования / анализа, - индуктивно и строится на конечном числе наблюдений, поэтому оно не полно и может быть недостоверно. Необходимо обоснование заключения, Т.е. тестирование результатов, на которых строится гипотеза, на статистическую достоверность. Достоверность непосредственно связана с репрезентативностью выборки, Т.е. с тем, насколько уверенно данные, полученные по выборке, позволяют судить о соответствующих параметрах генеральной совокупности. Целью исследования почти никогда не является изучение данной конкретной выборки; выборка представляет интерес лишь постольку, поскольку она дает информацию обо всей генеральной совокупности. Статистическая достоверность связи определяется тем, насколько вероятно, что обнаруженная в выборке связь подтвердится (будет вновь обнаружена) на другой выборке той же генеральной совокупности.

Основной задачей статистической проверки гипотез является репрезентативное выборочное описание свойств генеральных совокупностей. Для описания значительных по объему совокупностей свойств, состояний, процессов требуется накопление огромного выборочного материала или проведение исследований в национальном масштабе. Поэтому задача репрезентативного описания сводится к задаче проверки однородности выборочных описаний, полученных в разных исследованиях, и к объединению однородных данных.

Для проверки однородности, необходимы:

а) однообразность статистических описаний одних и тех же явлений разными авторами;

б) указание на величину объектов выборок, из которых вычислялись статистические оценки параметров и функций.

Начало любого исследования – это постановка проблемы. Самые простые, наивные вопросы являются прототипами проблемы.

В отличие от житейской, научная проблема формулируется в терминах определенной научной отрасли.

Постановка проблемы влечет за собой формулировку гипотезы. Гипотеза – это научное предположение, вытекающее из теории, которое еще не подтверждено и не опровергнуто. Научная гипотеза должна удовлетворять:

• принципам фальсифицируемости – быть опровергаемой в эксперименте; принцип фальсифицируемости абсолютен, так как опровержение теории всегда окончательно,

• принципам верифицируемости – быть подтверждаемой в эксперименте, этот принцип относителен, так как всегда есть вероятность опровержения гипотезы в следующем исследовании.

Различают научные и статистические гипотезы.

Научные гипотезы формулируются как предполагаемое решение проблемы.

Статистическая гипотеза – утверждение в отношении неизвестного параметра, сформулированное на языке математической статистики.

Любая научная гипотеза требует перевода на язык статистики. После проведения конкретного эксперимента проверяются многочисленные статистические гипотезы, поскольку в каждом исследовании регистрируется не один, а множество поведенческих параметров. Каждый параметр характеризуется несколькими статистическими мерами: центральной тенденции, изменчивости, распределения. Можно вычислить меры связи параметров и оценить значимость этих связей.

Экспериментальная гипотеза служит для организации эксперимента, а статистическая – для организации процедуры сравнения регистрируемых параметров.

Статистическая гипотеза необходима на этапе математической интерпретации данных эмпирических исследований. Большое количество статистических гипотез необходимо для подтверждения или опровержения основной – экспериментальной гипотезы. Экспериментальная гипотеза – первична, статистическая – вторична.

Процесс выдвижения и опровержения гипотез можно считать основным и наиболее творческим этапом деятельности исследователя. Установлено, что количество и качество гипотез определяется общей креативностью (общей творческой способностью) исследователя – «генератора идей».

Гипотеза может отвергаться, но никогда не может быть окончательно принятой. Любая гипотеза открыта для последующей проверки.

Формулирование гипотез систематизирует предположения исследователя и представляет их в четком и лаконичном виде.

Статистические гипотезы. В обычном языке слово «гипотеза» означает предположение.

В математической статистике термин «гипотеза» означает предположение, которое не только вызывает сомнения, но и которое мы собираемся в данный момент проверить.

При построении статистической модели приходиться делать много различных допущений и предположений, и далеко не все из них мы собираемся или можем проверить.

Статистическая проверка гипотезы состоит в выяснении того, насколько совместима эта гипотеза с имеющимся результатом случайного выбора.

Определение. Статистическая гипотеза – это предположение о распределении вероятностей, которое мы хотим проверить по имеющимся данным.

Гипотезы различают простые и сложные:

• простая гипотеза полностью задает распределение вероятностей;

• сложная гипотеза указывает не одно распределение, а некоторое множество распределений. Обычно это множество распределений, обладающих определенным свойством.

По содержанию статистические гипотезы подразделяются на виды:

· о законе распределения генеральной совокупности (например, гипотеза о том, что количество ошибок внимания у младших школьников имеет равномерное распределение);

· о числовых значениях параметров случайной величины (например, гипотеза о том, что среднее количество правильных ответов студентов контрольной группы на десять тестовых вопросов по теме равно восьми);

· об однородности выборок (т.е. принадлежности их одной и той же генеральной совокупности);

· о виде модели, описывающей статистическую зависимость между несколькими признаками (например, предположение о том, что связь между успешностью обучения математики 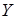и показателем невербального интеллекта учащихся 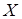линейная, прямо пропорциональная).

Статистические гипотезы подразделяются на нулевые и альтернативные.

Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезойи обозначают H₀.

В психологии принято считать, что 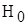– это гипотеза о сходстве, т.е. об отсутствии различий. Другими словами, это предположение о том, что все события, интересующие исследователя, произошли случайно, естественным образом. Обозначается нулевая гипотеза как .

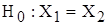Пример. Пусть исследователь сопоставляет значения некоторого признака развитости интеллекта (например, уровень вербального мышления) у двух групп подростков - из полных семей (первая группа) и неполных семей (вторая группа). Обозначим через 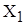и 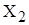случайные величины, показывающие значения признака (уровня вербального мышления). Тогда нулевая гипотеза означает предположение, что различий в показателе интеллекта у двух групп подростков.

Вместе с гипотезой H₀ выдвигается альтернативная или конкурирующаягипотеза, которая обозначается H₁, являющаяся логическим отрицанием 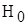. В паре они составляют две возможности выбора, осуществляемого в задачах проверки статистических гипотез. В альтернативной гипотезе 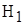предполагается, что события, интересующие исследователя, случайным образом произойти не могли, и имело место воздействие некоторого фактора.

Например:

1)	H0: x=0	2)	H0: Mx= 0	3)	H0: Mx= 0
	H1: Mx¹ 0		H1: Mx> 0		H1: Mx= 2

Если нулевая гипотеза 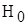говорит о «сходстве», то альтернативная гипотеза 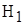– гипотеза «о различии», точнее, о значимости различий. Например, альтернативная гипотеза о том, что контрольные и экспериментальные группы различаются между собой по каким-либо значимым характеристикам.

Какая из этих гипотез более важна?

В психологии, как и в других науках, выявление различий более информативно в поиске нового, чем доказательство сходства. В психологии выявление различия разнообразных характеристик человека равносилен свидетельству его процесса развития, поэтому задача доказательства значимости различий (в терминах теории проверки гипотез – принятия альтернативной гипотезы) более существенна.

Проверка гипотез осуществляется с помощью критериев статистической оценки различий.

2. Статистические критерии

Для проверки любой статистической гипотезы выбирается какой-либо критерий, называемый критерием значимости - правило проверки статистической гипотезы.

Выдвинутую гипотезу проверяют на основе имеющейся выборки.

Суть проверки статистической гипотезы состоит в том, что для принятия или отклонения выдвинутой гипотезы используется специально составленная выборочная характеристика, случайная величина 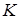, называемая критерием значимости. Она получена по выборке, и закон ее распределения считается известным (точно или приближенно). С помощью случайной величины 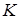по определенному правилу определяется «граница» между принятием и отклонением гипотезы. Поэтому термином «критерий» обозначают также правило, по которому принимается статистическое решение.

В основе большинства критериев значимости лежит следующий простой принцип: если сделана гипотеза о том, что событие имеет очень малую вероятность 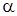(в психологии это обозначается часто 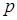), но в результате одного лишь испытания это событие произошло, то следует подвергнуть сомнению справедливость выдвинутой гипотезы.

Вероятность 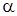практически невозможного события абстрактно выбирать нельзя. Ее значения диктуются реальной ситуацией. Например, если 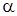- вероятность нераскрытия парашюта, то 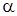должно быть десятичной дробью с большим количеством нулей после запятой. Это число обычно стандартизируется мировой практикой. Так же и в психологии.

Одно и то же эмпирическое значение критерия может оказаться значимым или незначимым в зависимости от количества наблюдений в выборке (n) или от так называемого количества степеней свободы, которое обозначается как ν.

Число степеней свободы. Число степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий относятся: объем выборки, средние и дисперсии.

Если мы расклассифицировали наблюдения по классам какой-либо номинативной шкалы и подсчитали количество наблюдений в каждой ячейке классификации, то мы получаем так называемый частотный вариационный ряд. Единственное условие, которое соблюдается при его формировании – объем выборки n.

Допустим у нас три класса: ″Умеет работать на ПК – умеет выполнять лишь определенные операции – не умеет работать″.

Выборка состоит из 50 человек. Если в первом классе – 20 человек, во втором классе – 20 человек, то в третьем должны оказаться 10 человек. Мы ограничены только одним условием – объемом выборки. Мы не свободны в определении количества испытуемых в третьем классе, ″свобода″ простирается только на первые два класса ν=с-1=3-1=2

Аналогичным образом, если бы у нас была классификация из 10 разрядов или классов, то мы были бы свободны только в 9 и т.д.

Зная n и/или число степеней свободы, по специальным таблицам можно определить критические значения критерия и сопоставить с ними полученное эмпирическое значение.

Среди возможных статистических критериев выделяют: односторонние и двусторонние, параметрические и непараметрические, более и менее мощные.

Односторонние и двусторонние. Понятие одностороннего либо двустороннего критерия связано с формулировкой гипотез. Если ″нулевая″ гипотеза формулируется о равенстве (Х1 = Х2), то для проверки используется двусторонний критерий. Если же ″нулевая″ гипотеза формулируется о неравенстве, то возможны три варианта:

1) если Х1≠Х2, то используется двусторонний критерий;

2) если Х1>Х2 или Х1<Х2, то односторонний критерий.

Параметрические критерии – это некоторые функции от параметров совокупности, они служат для проверки гипотез об этих параметрах или для их оценивания. Параметрические критерии включают в формулу расчета параметры распределения, т.е. средние и дисперсии.

Непараметрические критерии – это некоторые функции от функций распределения или непосредственно от вариационного ряда наблюдавшихся значений изучаемого случайного явления. Они служат только для проверки гипотез о функциях распределения или рядах наблюдавшихся значений.

Непараметрические критерии не включают в формулу расчета параметров распределения и основанные на оперировании частотами или рангами.

И те, и другие критерии имеют свои преимущества и недостатки.

Параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. Лишь с некоторой натяжкой мы можем считать данные, представленные в стандартизованных оценках, как интервальные. Кроме того, проверка распределения «на нормальность» требует достаточно сложных расчетов, результат которых заранее не известен.

Может оказаться, что распределение признака отличается от нормального, и нам так или иначе все равно придется обратиться к непараметрическим критериям.

Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном – с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака.

Применение критериев для принятия (отклонения) статистических гипотез всегда осуществляются с доверительной вероятностью, иначе говоря, на определенном уровне значимости

Уровень значимости – это вероятность того, что мы сочли различия существенными, а они на самом деле случайны.

Когда мы указываем, что различия достоверны на 5% уровне значимости, или при р≤0,05, то мы имеем ввиду, что вероятность того, что они недостоверны, составляет 0,05.

Если же мы указываем, что различия достоверны на 1% уровне значимости, или при р≤0,01, то имеем ввиду, что вероятность того, что они все-таки недостоверны равна 0,01.

Иначе, уровень значимости – это вероятность отклонения нулевой гипотезы, в то время как она верна.

Статистическая значимость это основной результат проверки статистической гипотезы.

Обоснование статистического вывода базируется на понятии уровня значимости. Уровень значимости это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности употребляют латинскую букву p.