Выбор меры центральной тенденции в зависимости от типа измерительной шкалы

Тип шкалы	Меры центральной тенденции
Номинальная	Мода
Ранговая	Мода, медиана
Интервальная	Мода, медиана, среднее
Отношений	Мода, медиана, среднее

Меры изменчивости признака

Меры изменчивости значений признака внутри группы оценивают разброс значений признака, вариативность.

Размахом выборки называют разность между наибольшим и наименьшим значениями признака в выборке: 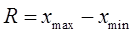. Размах измеряет на числовой шкале расстояние, в пределах которого изменяется варианта.

Выборочная дисперсия является мерой разброса значений признака относительного среднего значения.

Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений 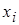от выборочной средней :

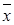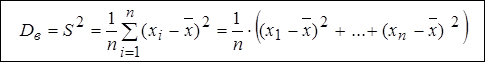
(для несгруппированных данных) .Здесь 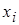- значение признака для дискретного вариационного ряда (или середина 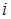-го интервала для интервального ряда).

Для сгруппированных данныхвыборочная дисперсия равна:

,

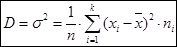где 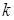- число групп признака (число частичных интервалов), 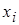- середина частичного интервала. Для практических вычислений более удобна формула

,

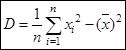которая для сгруппированных данных имеет вид

.

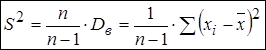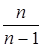Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия , где - поправочный коэффициент.

При больших 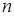значения 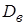и 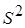будут мало отличаться, поэтому «исправление» выборочной дисперсии производят при малых 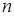( 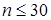). В целях повышения надежности полученной оценки следует увеличивать объем выборки.

Пример 1. При обследовании 50 членов семей получен дискретный вариационный ряд.

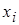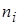Определите средний размер (среднее число членов) семьи.

Охарактеризуйте изменчивость размера семьи.

Объясните полученные результаты, сделайте выводы.

Решение

1. В данной задаче изучаемый признак является дискретным, так как размер семей не может отличаться друг от друга менее чем на одного человека. Рассчитаем среднее число членов семьи:

.

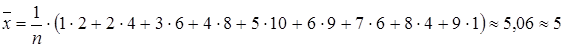Средний размер семьи около 5 человек.

2. Для расчета дисперсии используем формулу :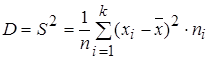

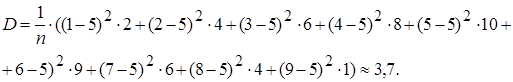
Дисперсия размера семьи – 3,7 ( ).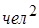

Найдем среднее квадратическое отклонение размера семьи: 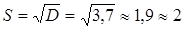. Среднее квадратическое отклонение размера семьи - 2 человека.

Найдем коэффициент вариации размера семьи по формуле 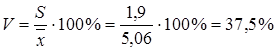. Коэффициент вариации составляет 38%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность семей является неоднородной, чем объясняется высокая изменчивость размера семьи в данной совокупности.

Стандартным (средним квадратическим) отклонением (С.к.о.) 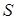признака называется положительное значение квадратного корня из выборочной дисперсии:

.

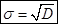С.к.о. полно характеризует разброс значений относительно средней арифметической. Выборочное с.к.о. – мера абсолютной изменчивости признака и выражается в тех же единицах измерения, в которых выражен изучаемый признак. Поэтому по с.к.о. можно сравнивать изменчивость лишь одних и тех же показателей, а сопоставлять с.к.о. разных признаков по абсолютной величине нельзя.

Для того чтобы сравнить по уровню изменчивости признаки, выраженные в различных единицах измерения, применяют коэффициент вариации:

,

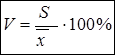где 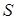- стандартное отклонение, 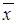- среднее арифметическое.