Лекция 3. числовые характеристики выборки

План:

1. Структурирование, ввод и проверка данных

2. Меры центральной тенденции

Структурирование, ввод и проверка данных.

Прежде чем мы сможем применить статистические методы или строить графики, следует представить собранные данные в форме, пригодной для обработки. При этом рекомендуется придерживаться следующего плана действий:

· Проведите структурирование набора данных; прежде всего, выясните, к каким категориям относятся наблюдения и переменные. В большинстве случаев это ясно сразу. Определите шкалу, к которой относятся переменные.

· Составьте таблицу исходных данных. Каждая строка такой таблицы обычно соответствует одному объекту, а каждый столбец – одному измеренному признаку.

· Введите данные, учитывая таблицу исходных данных. Не вводите данные, которые можно вычислить на основе других данных. Эти вычисления следует предоставить компьютеру.

· Проверьте введенные данные на отсутствие ошибок и осмысленность.

· Теперь можно начинать статистическую обработку введенных данных.

Группировка и построение частотного распределения – первый шаг статистического анализа полученных данных. Следующий шаг – получение числовых характеристик выборки.

Меры центральной тенденции

При исследовании массивов данных мы чаще всего оперируем величинами, характеризующими этот массив, именно по ним делаем вывод обо всей совокупности данных. К таким характеристикам относятся меры центральной тенденции, то есть значение наиболее часто встречающееся в данной совокупности.

Основной характеристикой вариационного ряда является его среднееарифметическое. Это типическая характеристика всей совокупности. Она уничтожает, погашает, сглаживает влияние индивидуальных особенностей и позволяет представить в одной величине некоторую общую характеристику реальной совокупности.

Для дискретного выборочного ряда среднее арифметическое 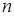значений 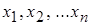(или выборочное среднее значение) равно

.

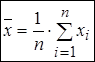Чтобы подсчитать среднее арифметическое, надо суммировать все значения ряда и разделить сумму на количество суммированных значений

Если числа в выборке повторяются, например, 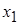- 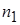раз, 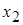- 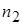раз, …, 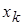- 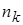раз, причем 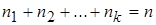, то для сгруппированных выборочных данных выборочное среднее равно

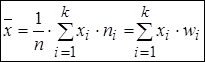
и называется взвешенным средним. Для интервального вариационного ряда за 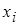принимают середину 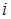-го интервала.

Среднее арифметическое имеет двойной смысл:

1) оно может быть средним значением признака в данной совокупности (средняя зарплата отдела);

2) это приближенное значение постоянной величины, подвергающейся изменениям (рост человека).

Свойства среднего

1. Сумма всех n-отклонений от значения среднего должно быть равно нулю, то есть: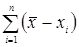

2. Если константу прибавить к каждому значению, то среднее увеличивается на ту же константу.

3. Если каждое значение умножить на константу, то среднее то же будет умножено на эту константу.

4. Сумма квадратов отклонений значений от их среднего меньше суммы квадратов отклонений от любой другой точки, то есть: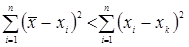

Модой называется числовое значение признака, которое встречается в выборке с наибольшей частотой (обозначается ).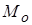

Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).

Соглашения по поводу моды

· Если все значения в группе встречаются одинокого часто, считают, что у данной группы, моды нет.

· Когда два соседних значения имеют одинаковую частоту и эти частоты больше любых других частот в группе, то модой считают среднее от этих двух значений.

· Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этой группы есть две моды, такая группа называется бимодальной. Бимодальной называется группа и в том случае, если эти две черты не совсем равны. В таких случаях договорились различать большую и малую моду и во всей группе, наряду с одной большой модой может быть несколько меньших мод.

Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»).

Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтение или отношение к чему-то, то мультимодальность может означать, что существуют несколько определенно различных мнений.

Мультимодальность также служит индикатором того, что выборка не является однородной и наблюдения, возможно, порождены двумя или более «наложенными» распределениями. В отличие от среднего арифметического, выбросы на моду не влияют. Для непрерывно распределенных случайных величин, например, для показателей среднегодовой доходности взаимных фондов, мода иногда вообще не существует (или не имеет смысла). Поскольку эти показатели могут принимать самые разные значения, повторяющиеся величины встречаются крайне редко.

Медианой называется значение признака, которое делит упорядоченное множество данных пополам по объему (обозначается ).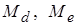

Если число членов ряда нечетное ( 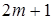), то серединой ряда будет значение 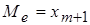. Если число членов ряда четное ( 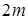), то за медиану обычно принимают .

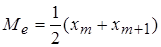Отметим некоторые особенности рассмотрения мер центральной тенденции.

1. В небольших выборках мода может быть совершенно нестабильной.

2. На медиану не влияют величины самых больших и самых малых значений.

3. На величину среднего значения оказывает влияние каждый элемент выборки, если какой-либо элемент выборки изменится на величину с, то среднее значение изменится в том же направлении, на величину с/n.

4. Некоторые выборки вообще нельзя охарактеризовать с помощью мер центральной тенденции. Особенно это справедливо для выборок, имеющих более, чем 1 моду.

5. Если выборка является унимодальной, т.е. имеет 1 моду и гистограмма такой выборки является симметричной, то в этом случае мода, медиана и среднее значение совпадают.

В табл. 2 приводятся данные о возможности использования тех или иных мер центральной тенденции в зависимости от типа измерительных шкал.

Таблица 2