Лекция 1. Психология и математика

КОНСПЕКТЫ ЛЕКЦИЙ

Измерительные шкалы

Введем некоторые определения.

Признаки и переменные – это измеряемые явления. Такими явлениями могут быть время решения задачи, количество ошибок.

Значения признака определяются при помощи специальных шкал наблюдения.

Переменные являются случайными величинами, поскольку неизвестно заранее, какое именно значение они примут.

Измерение – это приписывание числовых форм объектам или событиям в соответствии с определенными правилами.

Классификация шкал измерения:

1) номинативная, или номинальная, или шкала наименований;

2) порядковая, или ординальная, шкала;

3) интервальная, или шкала равных интервалов;

4) шкала равных отношений.

Номинальная шкала –это шкала, классифицирующая по названию. Название же не измеряется количественно, оно лишь позволяет отличить один объект от другого или одного субъекта от другого. Номинативная шкала – это способ классификации объектов или субъектов, распределения их по ячейкам классификации.

Простейший случай номинативной шкалы – дихотомическая шкала, состоящая всего лишь из двух ячеек, например: «имеет братьев и сестер – единственный ребенок в семье»; «иностранец – соотечественник»; «проголосовал «за» – проголосовал «против»» и т.п.

Расклассифицировав все объекты, реакции или испытуемых, можно перейти, от наименований к числам, подсчитав количество наблюдений в каждом классе. Номинальная шкала позволяет подсчитывать частоты встречаемости разных наименований или значений признака и затем работать с этими частотами. Единица измерения, которой мы оперируем – это одно наблюдение.

Операции с числами для номинативной шкалы.

1) Нахождение частот распределения по пунктам шкалы с помощью процентирования или в натуральных единицах. Нетрудно подсчитать численность каждой группы и отношение этой численности к общему ряду распределения (частоты).

2) Поиск средней тенденции по модальной частоте. Модальной (Мо) называют группу с наибольшей численностью. Эти две операции дают представление о распределении психологических характеристик в количественных показателях. Его наглядность повышается отображением в диаграммах.

3) Самым сильным способом количественного анализа является установление взаимосвязи между рядами свойств, расположенных неупорядоченно. С этой целью составляют перекрестные таблицы. Помимо простой процентовки в таблицах перекрестной классификации можно подсчитать критерий сопряженности признаков по Пирсону.

Порядковая шкала – это шкала, классифицирующая по принципу «больше – меньше». Если в шкале наименований было безразлично, в каком порядке расположены классификационные ячейки, то в порядковой шкале они образуют последовательность от ячейки «самое малое значение» к ячейке «самое большое значение» (или наоборот).

Это полностью упорядоченная шкала наименований, она устанавливает отношения равенства между явлениями в каждом классе и отношения последовательности в понятиях больше, меньше между всеми без исключения классами.

В порядковых измерениях символы, в частности числа, присваивают классам объектов так, чтобы первые отображали не только равенство или неравенство, эквивалентность или неэквивалентность, но и упорядоченность объектов в отношении измеряемого свойства. В шкалах порядка классы объектов, как и в случае шкал наименований, являются дискретными. И хотя цифры, обозначающие классы можно сравнивать, всегда надо помнить, что в шкалах порядка они используются только в целях кодирования.

Интервалы в этой шкале не равны, поэтому числа обозначают лишь порядок следования признаков. И операции с числами – это операции с рангами, но не с количественным выражением свойств в каждом пункте.

1) Числа поддаются монотонным преобразованиям: их можно заменить другими с сохранением прежнего порядка. Так вместо ранжирования от 1 до 5 можно упорядочить тот же ряд в числах от 2 до10. Отношения между рангами останутся неизменными.

2) Суммарные оценки по ряду упорядоченных номинальных шкал – хороший способ измерять одно и то же свойство по набору различных индикаторов.

3) Для работы с материалом, собранным по упорядоченной шкале, можно использовать, помимо модальных показателей (Мо), поиск средней тенденции с помощью медианы (Ме), найти среднее арифметической (М) и сделать оценку разброса данных с помощью дисперсии (D) и стандартного отклонения (σ).

4) Наиболее сильный показатель для таких шкал – корреляция рангов по Спирмену или по Кендаллу. Ранговые корреляции указывают на наличие или отсутствие функциональных связей в двух рядах признаков, измеренных упорядоченными шкалами

Интервальная шкала – это шкала, классифицирующая по принципу «больше на определенное количество единиц – меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии.

Шкала интервалов представляет собой полностью упорядоченный ряд с измеренными интервалами между пунктами, причем отсчет начинается с произвольно от выбранной величины (нет абсолютного нуля).

При конструировании шкалы интервалов используют три произвольные операции:

1. установление величин единиц измерения;

2. определение нулевой точки;

3. определение направления, в котором ведут отсчет по отношению к нулевой точке

Операции с числами в интервальной метрической шкале богач, чем в номинальных шкалах.

1. Точка отсчета на шкале выбирается произвольно.

2. Используются все методы описательной статистики. Возможности корреляционного и регрессионного анализа. Можно использовать коэффициент парной корреляции Пирсона и коэффициенты множественной корреляции, что может предсказать изменения в одной переменной в зависимости от изменений в другой или в целом ряде переменных.

Шкала равных отношений –это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства.

Конструирование шкал отношений предполагает наряду с наличием свойств предыдущих шкал существование постоянной естественной нулевой точки отсчета, в которой измеряемый признак полностью отсутствует.

Шкалы отношений характеризуются тем, что в них:

1. классы объектов разделены и упорядочены согласно измеряемому свойству;

2. равным разностям между классами объектов соответствуют равные разности между приписываемыми им числами;

3. числа, приравниваемые классам объектов, пропорциональны степени выраженности измеряемого свойства. Последнее не было свойственно рассмотренным выше шкалам.

Основными операциями, допустимыми на уровне шкал отношений, являются все те операции, которым подчиняются шкалы всех перечисленных выше типов, и дополнительно — операции установления равенства отношений между отдельными значениями шкалы. Это возможно благодаря существованию на шкале естественного, абсолютного нуля. Поэтому лишь для данной шкалы числа, являющиеся точками (значениями) на шкале, соответствуют реальному количеству измеряемого свойства, что позволяет производить с ними любые арифметические действия — оперирование суммами, произведениями и частными.

Применение математических методов к неадекватным данным приводит к странным, а часто и ложным результатам.

1) Первое ограничение – соразмерность количественных показателей, фиксированных разными шкалами в рамках одного исследования. Более сильная шкала отличается от слабой тем, что допускает более широкий диапазон математических операций с числами. Все, что допустимо для слабой шкалы допустимо и для более сильной, но не наоборот. Поэтому, смешение в анализе мерительных эталонов разного типа приводит к тому, что не используются возможности сильных шкал.

2) Второе ограничение связано с формой распределения величины фиксированных описанными выше шкалами, которое предполагается нормальным..

1. Классификация психологических задач, решаемых с помощью статистических методов.

Прежде, чем выполнить любой психологический эксперимент, необходимо четко сформулировать его задачи, определить экспериментальную гипотезу и все этапы ее статистической проверки, а также выбрать соответствующий статистический метод, наиболее эффективный для решения поставленных в исследовании задач.

Подавляющее большинство задач, решаемых психологом в эксперименте, предполагает те или иные сопоставления. Это могут быть сопоставления одних и тех же показателей в разных группах испытуемых или, напротив, разных показателей в одной и той же группе. Для определения степени эффективности каких-либо воздействий (обучение, тренировка, тренинг, инструктаж) сравниваются показатели «до» и «после» этих воздействий.

Например, сравниваются показатели уровня агрессивности у подростков до и после психотренинга, что позволяет определить его эффективность. Или в лонгитюдном исследовании сопоставляются результаты у одних и тех же испытуемых по одним и тем же методикам, но в разном возрасте, это позволяет выявить временную динамику анализируемых показателей.

Иногда возникает задача сравнить индивидуальные показатели, полученные при различных внешних условиях, для выявления связи между показателями и факторов, объединяющих эти связи.

Два выборочных распределения сравниваются между собой или с теоретическим законом распределения, чтобы выявить различия или, напротив, сходство в типах распределении.

Например, сравнение распределении времени решения простой и сложных задач позволит построить классификацию задач и типологию испытуемых.

Психологические задачи, решаемые с помощью методов математической статистики, условно можно разделить на несколько групп.

1. Задачи, требующие установления сходства или различия.

2. Задачи, требующие группировки и классификации данных.

3. Задачи, ставящие целью анализ источников вариативности получаемых психологических признаков.

4. Задачи, предполагающие возможность прогноза на основе имеющихся данных.

Меры центральной тенденции

При исследовании массивов данных мы чаще всего оперируем величинами, характеризующими этот массив, именно по ним делаем вывод обо всей совокупности данных. К таким характеристикам относятся меры центральной тенденции, то есть значение наиболее часто встречающееся в данной совокупности.

Основной характеристикой вариационного ряда является его среднееарифметическое. Это типическая характеристика всей совокупности. Она уничтожает, погашает, сглаживает влияние индивидуальных особенностей и позволяет представить в одной величине некоторую общую характеристику реальной совокупности.

Для дискретного выборочного ряда среднее арифметическое 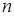значений 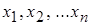(или выборочное среднее значение) равно

.

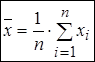Чтобы подсчитать среднее арифметическое, надо суммировать все значения ряда и разделить сумму на количество суммированных значений

Если числа в выборке повторяются, например, 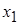- 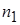раз, - раз, 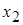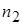…, - раз, 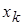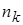причем 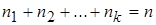, то для сгруппированных выборочных данных выборочное среднее равно

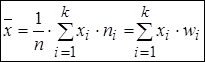
и называется взвешенным средним. Для интервального вариационного ряда за 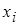принимают середину 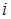-го интервала.

Среднее арифметическое имеет двойной смысл:

1) оно может быть средним значением признака в данной совокупности (средняя зарплата отдела);

2) это приближенное значение постоянной величины, подвергающейся изменениям (рост человека).

Свойства среднего

1. Сумма всех n-отклонений от значения среднего должно быть равно нулю, то есть: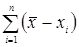

2. Если константу прибавить к каждому значению, то среднее увеличивается на ту же константу.

3. Если каждое значение умножить на константу, то среднее то же будет умножено на эту константу.

4. Сумма квадратов отклонений значений от их среднего меньше суммы квадратов отклонений от любой другой точки, то есть: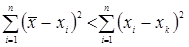

Модой называется числовое значение признака, которое встречается в выборке с наибольшей частотой (обозначается ).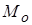

Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).

Соглашения по поводу моды

· Если все значения в группе встречаются одинокого часто, считают, что у данной группы, моды нет.

· Когда два соседних значения имеют одинаковую частоту и эти частоты больше любых других частот в группе, то модой считают среднее от этих двух значений.

· Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этой группы есть две моды, такая группа называется бимодальной. Бимодальной называется группа и в том случае, если эти две черты не совсем равны. В таких случаях договорились различать большую и малую моду и во всей группе, наряду с одной большой модой может быть несколько меньших мод.

Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»).

Мультимодальность распределения дает важную информацию о природе исследуемой переменной. Например, в социологических опросах, если переменная представляет собой предпочтение или отношение к чему-то, то мультимодальность может означать, что существуют несколько определенно различных мнений.

Мультимодальность также служит индикатором того, что выборка не является однородной и наблюдения, возможно, порождены двумя или более «наложенными» распределениями. В отличие от среднего арифметического, выбросы на моду не влияют. Для непрерывно распределенных случайных величин, например, для показателей среднегодовой доходности взаимных фондов, мода иногда вообще не существует (или не имеет смысла). Поскольку эти показатели могут принимать самые разные значения, повторяющиеся величины встречаются крайне редко.

Медианой называется значение признака, которое делит упорядоченное множество данных пополам по объему (обозначается ).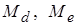

Если число членов ряда нечетное ( 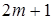), то серединой ряда будет значение 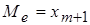. Если число членов ряда четное ( 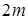), то за медиану обычно принимают .

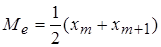Отметим некоторые особенности рассмотрения мер центральной тенденции.

1. В небольших выборках мода может быть совершенно нестабильной.

2. На медиану не влияют величины самых больших и самых малых значений.

3. На величину среднего значения оказывает влияние каждый элемент выборки, если какой-либо элемент выборки изменится на величину с, то среднее значение изменится в том же направлении, на величину с/n.

4. Некоторые выборки вообще нельзя охарактеризовать с помощью мер центральной тенденции. Особенно это справедливо для выборок, имеющих более, чем 1 моду.

5. Если выборка является унимодальной, т.е. имеет 1 моду и гистограмма такой выборки является симметричной, то в этом случае мода, медиана и среднее значение совпадают.

В табл. 2 приводятся данные о возможности использования тех или иных мер центральной тенденции в зависимости от типа измерительных шкал.

Таблица 2

Меры изменчивости признака

Меры изменчивости значений признака внутри группы оценивают разброс значений признака, вариативность.

Размахом выборки называют разность между наибольшим и наименьшим значениями признака в выборке: 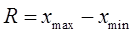. Размах измеряет на числовой шкале расстояние, в пределах которого изменяется варианта.

Выборочная дисперсия является мерой разброса значений признака относительного среднего значения.

Выборочная дисперсия – это среднее арифметическое квадратов отклонений значений 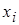от выборочной средней :

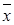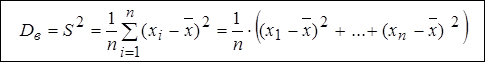
(для несгруппированных данных) .Здесь 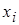- значение признака для дискретного вариационного ряда (или середина 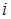-го интервала для интервального ряда).

Для сгруппированных данныхвыборочная дисперсия равна:

,

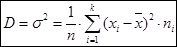где 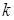- число групп признака (число частичных интервалов), 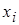- середина частичного интервала. Для практических вычислений более удобна формула

,

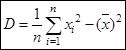которая для сгруппированных данных имеет вид

.

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия 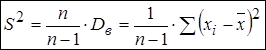, где 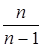- поправочный коэффициент.

При больших 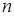значения 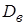и 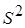будут мало отличаться, поэтому «исправление» выборочной дисперсии производят при малых 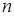( 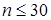). В целях повышения надежности полученной оценки следует увеличивать объем выборки.

Пример 1. При обследовании 50 членов семей получен дискретный вариационный ряд.

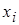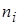Определите средний размер (среднее число членов) семьи.

Охарактеризуйте изменчивость размера семьи.

Объясните полученные результаты, сделайте выводы.

Решение

1. В данной задаче изучаемый признак является дискретным, так как размер семей не может отличаться друг от друга менее чем на одного человека. Рассчитаем среднее число членов семьи:

.

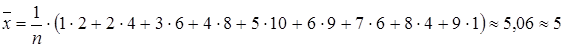Средний размер семьи около 5 человек.

2. Для расчета дисперсии используем формулу :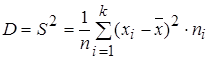

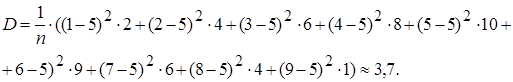
Дисперсия размера семьи – 3,7 ( ).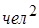

Найдем среднее квадратическое отклонение размера семьи: 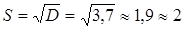. Среднее квадратическое отклонение размера семьи - 2 человека.

Найдем коэффициент вариации размера семьи по формуле 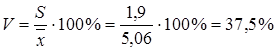. Коэффициент вариации составляет 38%. Так как коэффициент вариации больше 35%, можно сделать вывод о том, что изучаемая совокупность семей является неоднородной, чем объясняется высокая изменчивость размера семьи в данной совокупности.

Стандартным (средним квадратическим) отклонением (С.к.о.) 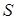признака называется положительное значение квадратного корня из выборочной дисперсии:

.

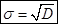С.к.о. полно характеризует разброс значений относительно средней арифметической. Выборочное с.к.о. – мера абсолютной изменчивости признака и выражается в тех же единицах измерения, в которых выражен изучаемый признак. Поэтому по с.к.о. можно сравнивать изменчивость лишь одних и тех же показателей, а сопоставлять с.к.о. разных признаков по абсолютной величине нельзя.

Для того чтобы сравнить по уровню изменчивости признаки, выраженные в различных единицах измерения, применяют коэффициент вариации:

,

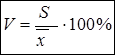где 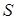- стандартное отклонение, 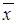- среднее арифметическое.

Коэффициент эксцесса

Понятие «эксцесс» применимо лишь к одномодальным распределениям и относится к крутизне кривой в окрестности единственной моды. (Если распределение имеет две моды, то принято говорить об эксцессе кривой в окрестности каждой моды.)

Коэффициент эксцесса (островершинности) кривой распределения равен:

Первая кривая (А) является совсем острой: подобная кривая называется островершинной. Вторая (Б) — сравнительно плоская: такие кривые называются плосковершин­ными. «Островершинность», или степень эксцесса, третьей кривой (В) представляет собой норму, по отношению к которой изме­ряется эксцесс других кривых. Третья кривая на рис. 1.3 — нормальная кривая, принято говорить, что она является средневершинной.

Анализ эксцесса кривой распределения позволяет сделать следующие выводы в зависимости от формы распределения показателей (данных, вариант) психологического признака. В случае, когда возникает значительный положительный эксцесс и вся масса баллов скучивается вблизи среднего значения, возможны следующие объяснения: - ключ составлен неверно; - испытуемые разгадали направленность теста (опросника).

Теоретически величина эксцесса может варьировать от – 3 до + ¥. Критерий согласия с нормальным распределением аналогично коэффициенту асимметрии определяется по таблицам граничных значений. Например, для n = 100 и b₁ = 0,95 Ex_кр = 0,83 (см. Приложение, табл. II).

Аналогично определению асимметрии распределение соответствует нормальному (согласуется с нормальным), если Ex < Ex_кр. При обратном соотношении принято говорить, что по показателю эксцесса эмпирическое распределение статистически достоверно отличается от нормального.

Отрицательный эксцесс может образовать две вершины, две моды (с «провалом» между ними). Это указывает на то, что выборка испытуемых разделилась на две категории: одни справились с большинством заданий, другие – не справились. Значит, в основе заданий имеется какой-то общий для них признак, соответствующий определенному свойству испытуемых. Если у испытуемых есть это свойство (способность, знание, умение), то они справляются с большинством заданий, если нет свойства, то не справляются.

Порядок действий

Шаг 1. Формулируются нулевая и альтернативная гипотезы.

Нулевая гипотеза .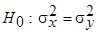

Альтернативная гипотеза .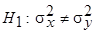

Шаг 2. Задается уровень значимости .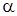

Шаг 3. По независимым выборкам объемов 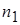и 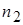вычисляются выборочные дисперсии:

; .

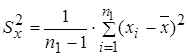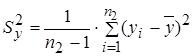Шаг 4. Вычисляется эмпирическое значение критерия

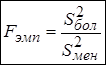(5.9)

– отношение большей выборочной дисперсии к меньшей выборочной дисперсии. Отсюда следует, что значение 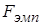всегда будет больше или равно единице: .

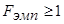Шаг 5. Для альтернативной гипотезы 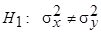критическая область двусторонняя. Ее границы определяются двумя числами, которые находятся по таблице и зависят от уровня значимости 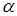и числа степеней свободы 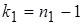(для большей дисперсии) и 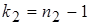(для меньшей дисперсии). Это числа

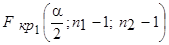и .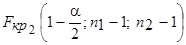

Правую точку 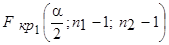в 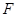-распределении можно определить непосредственно по таблице. Левая точка связана с правой следующим образом:

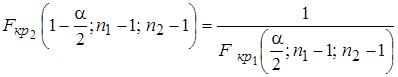. (5.10)

Шаг 6. Гипотеза 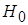о равенстве дисперсий принимается, если 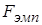попало в область допустимых значений

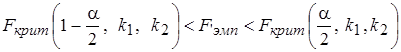. (5.11)

В этом случае делается вывод, что различие выборочных дисперсий незначимо и объясняется случайными причинами, в частности, случайным отбором объектов выборки.

Если нулевая гипотеза отвергнута, то можно утверждать, что различие выборочных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны.

Замечания.

1. Вопрос о том, какую выборку обозначать первым или вторым номером, обычно решается произвольно. В качестве первой выборки обычно берется та, для которой вычисленная выборочная дисперсия больше.

2. В прошлом было принято проверять гипотезу 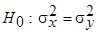до проверки по 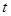-критерию гипотезы 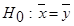. В учебниках советовали не приступать к испытанию по 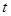-критерию, если отношение 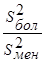привело к отклонению гипотезы о равенстве дисперсий. Однако это не так.

Более важным условием является нормальность совокупностей, поскольку отсутствие нормальности совокупностей не увеличивает обоснованности применения 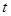-критерия. Но при отсутствии нормальности совокупностей проверка предположения об однородности дисперсий может оказаться необоснованной. Предположение об извлечении выборок из нормальной совокупности нельзя принять необдуманно в случае гипотез о генеральных дисперсиях, в отличие от проверки гипотез относительно средних по критерию Стьюдента [1, с. 276-278].

3. При равных объемах совокупностей 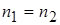нет оснований говорить о нарушении допущения об однородных дисперсиях. Однако если точно установлено, что совокупности описываются нормальным законом, а 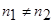, то стоит специально проверить гипотезу о равенстве дисперсий еще до проверки гипотезы о равенстве средних.

4. В случае зависимых выборок проверка гипотезы о равенстве дисперсий осуществляется с помощью другого критерия. Его описание можно найти в книге [1, с. 279].

2. Пример применения критерия 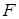- Фишера

Задача 3.При решении задачи об уровне интеллекта в двух группах по признаку 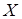«число правильных ответов на тестовые задания» выяснилось, что нет оснований для отклонения гипотезы о равенстве средних значений признака в двух группах. Однако психолога заинтересовал вопрос: есть ли различия в степени изменчивости показателей умственного развития между группами?

Решение

Получены следующие данные: в первой группе 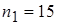, , 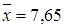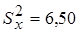; во второй группе , , .

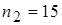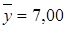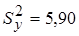Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в группах. Выдвинем нулевую гипотезу 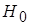о равенстве генеральных двух дисперсий, т.е. : .

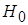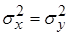Поскольку исследователя интересует только, имеются ли различия в степени изменчивости показателей, но не интересует, в какой группе она больше, то альтернативная гипотеза 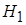: 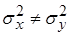, в этом случае критическая область двусторонняя. Уровень значимости принимаем 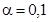; число степеней свободы равно , .

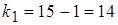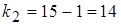По таблице распределения Фишера находим правую критическую точку 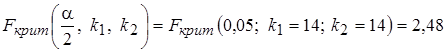. Тогда значение левой критической точки найдем по формуле (5.10):

.

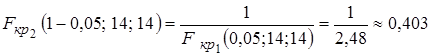Вычислим эмпирическое значение 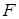-критерия

.

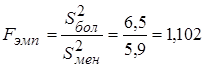Так как 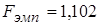удовлетворяет неравенству 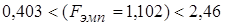, то 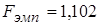попало в область допустимых значений. Значит, нет оснований на уровне значимости 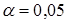отвергнуть нулевую гипотезу о равенстве дисперсий.

Психолог может утверждать, что нет различия между выборками из двух групп по степени изменчивости показателя «умственное развитие».

Ранговая корреляция

Вычисление ранговой корреляции позволяет определить силу и направление корреляционной связи между двумя признаками, измеренными в ранговой шкале или между двумя иерархиями признаков. При этом по каждой переменной должно быть представлено не менее 5 наблюдений. Для вычисления ранговой корреляции используют 2 метода: вычисление коэффициента Спирмена и коэффициента Кенделла. Какой из этих двух методов использовать, зависит от предпочтения исследователя.

ПРИЛОЖЕНИЕ

СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ

Таблица I

Критические значения коэффициента асимметрии (As),

используемого для проверки гипотезы о нормальности распределения

Объём выборки	Уровни Значимости	Объём выборки	Уровни значимости	Объём выборки	Уровни Значимости
0,95	0,99	0,95	0,99	0,95	0,99
	0,71 0,66 0,62 0,59 0,56 0,53 0,49 0,46 0,43 0,41	1,06 0,98 0,92 0,87 0,82 0,79 0,72 0,67 0,63 0,60		0,39 0,35 0,32 0,30 0,28 0,25 0,23 0,21 0,20 0,19	0,57 0,51 0,46 0,43 0,40 0,36 0,33 0,30 0,28 0,27		0,18 0,17 0,16 0,16 0,15 0,15 0,14 0,14 0,13 0,13	0,26 0,24 0,23 0,22 0,22 0,21 0,20 0,20 0,19 0,18

Таблица II

Уровень значимости различий

Пирсона и Спирмена

Степени свободы n – 2	Уровень значимости	Степени свободы n – 2	Уровень значимости	Степени свободы n – 2	Уровень значимости
0,95	0,99	0,95	0,99	0,95	0,99
	0,75 0,71 0,67 0,63 0,60 0,58 0,55 0,53 0,51 0,50 0,48 0,47 0,46 0,44 0,43	0,87 0,83 0,80 0,77 0,74 0,71 0,68 0,66 0,64 0,62 0,61 0,59 0,58 0,56 0,55		0,42 0,41 0,40 0,40 0,39 0,38 0,37 0,37 0,36 0,36 0,35 0,33 0,30 0,29 0,27	0,54 0,53 0,52 0,51 0,50 0,49 0,48 0,47 0,46 0,46 0,45 0,42 0,39 0,37 0,35		0,25 0,23 0,22 0,21 0,20 0,17 0,16 0,14 0,11 0,10 0,09 0,07 0,06 0,06	0,33 0,30 0,28 0,27 0,25 0,23 0,21 0,18 0,15 0,13 0,12 0,10 0,09 0,09

Таблица XIV

Критические значения коэффициента t Кендалла

Объем выборки	Уровни значимости	Объем выборки	Уровни значимости
0,95	0,99	0,999	0,95	0,99	0,999
	0,91 0,77 0,71 0,61 0,56 0,51 0,48 0,45	0,98 0,87 0,79 0,72 0,67 0,63 0,59	0,99 0,91 0,84 0,79 0,75		0,43 0,41 0,39 0,38 0,36 0,35 0,34 0,33	0,56 0,54 0,51 0,49 0,47 0,46 0,44 0,43	0,71 0,68 0,65 0,62 0,60 0,58 0,56 0,54

КОНСПЕКТЫ ЛЕКЦИЙ

Лекция 1. Психология и математика

Существует мнение, неоднократно высказывавшееся круп­ными учеными прошлого: область знания становится наукой, лишь применяя математику. С этим мнением, возможно, не со­гласятся многие гуманитарии. А зря: именно математика позво­ляет количественно сравнивать явления, проверять правильность словесных утверждений и тем самым добираться до истины либо приближаться к ней. Математика делает обозримыми длинные и подчас туманные словесные описания, проясняет и экономит мысль.

Математические методы позволяют обоснованно прогно­зировать будущие события, вместо того, чтобы гадать на кофей­ной гуще или как-либо иначе. В общем, польза от применения математики велика, но и труда на ее освоение требуется много. Однако он окупается сполна.

Психология в своем научном становлении неизбежно должна была пройти и прошла путь математизации, хотя не во всех стра­нах и не в полной мере. Точной даты начала пути математизации, пожалуй, не знает ни одна наука. Однако для психологии в каче­стве условной даты начата этого пути можно принять 18 апреля

1822 г. Именно тогда в Королевском немецком научном обществе Иоганн Фридрих Гербарт прочел доклад «О возможности и необ­ходимости применять в психологии математику». Основная идея доклада сводилась к упомянутому выше мнению: если психоло­гия хочет быть наукой, подобно физике, в ней нужно и можно применять математику.

Спустя два года после этого программного по своей сути док­лада И. Ф. Гербарт издал книгу «Психология как наука, заново ос­нованная на опыте, метафизике и математике». Эта книга приме­чательна во многих отношениях. Она, на мой взгляд (см. Г.В Суходольский, [8]), явилась пер­вой попыткой создания психологической теории, опирающейся на тот круг явлений, которые непосредственно доступны каждо­му субъекту, а именно на поток представлений, сменяющих друг друга в сознании. Никаких эмпирических данных о характеристиках этого потока, полученных, подобно физике, эксперимен­тальным путем, тогда не существовало. Поэтому Гербарт в отсут­ствие этих данных, как он сам писал, должен был придумывать гипотетические модели борьбы всплывающих и исчезающих в сознании представлений. Облекая эти модели в аналитическую форму,например φ =α(l-exp[-βt]) ,где t—время, φ—скорость изменения представлений, α и β — константы, зависящие от опы­та, Гербарт, манипулируя числовыми значениями параметров, пы­тался описать возможные ха